相似性搜索：第 7 部分--LSH 组合物

S相似性搜索是一个问题，给定一个查询，目标是在所有数据库文档中找到与其最相似的文档。

一、说明

在数据科学中，相似性搜索经常出现在 NLP 领域、搜索引擎或推荐系统中，其中需要检索最相关的文档或项目以进行查询。有多种不同的方法可以提高海量数据的搜索性能。

在本系列文章的最后两部分中，我们深入研究了 LSH——一种将输入向量转换为低维哈希值，同时保留有关其相似性的信息的算法。

特别是，我们已经研究了两种适用于不同距离度量的算法：

相似性搜索：第 5 部分--局部敏感哈希（LSH）

相似性搜索：第 6 部分--LSH 森林的随机投影

随机投影方法构建了保持向量余弦相似性的超平面森林。

事实上，LSH 算法也适用于其他距离度量。尽管每种方法都有其独特的部分，但每种方法中都出现了许多共同的概念和公式。为了促进未来新方法的学习过程，我们将更多地关注理论并提供一些经常出现在高级 LSH 文献中的基本定义和定理。在本文结束时，我们将能够通过简单地将基本方案组合为乐高积木来构建更复杂的 LSH 方案。

最后我们将了解如何将欧几里得距离纳入 LSH 中。

注意。作为主要先决条件，您应该已经熟悉本系列文章的第 5 部分和第 6 部分。如果没有，强烈建议先阅读它们。

注意。余弦距离正式定义在 [0, 2] 范围内。为简单起见，我们将其映射到区间 [0, 1]，其中 0 和 1 分别表示最低和最高可能的相似度。

二、LSH 的正式定义

给定距离度量 d，如果对于随机选择的对象 x 和 y，满足以下条件，则 H 被称为 (d₁, d2, p₁, p2) 敏感的 LSH 函数：

如果 d(x, y) ≤ d₁，则 p(H(x) = H(y)) ≥ p₁，即 H(x) = H(y) 的概率至少为 p₁。
如果 d(x, y) ≥ d2，则 p(H(x) = H(y)) ≤ p2，即 H(x) = H(y) 的概率至多为 p2。

让我们了解这些陈述的含义。当两个向量相似时，它们之间的距离较小。基本上，第一个语句确保将它们散列到同一存储桶的概率高于某个阈值。这样，就消除了一些漏报：如果两个向量之间的距离大于d₁，那么它们散列到同一桶的概率始终小于p₁。相反，第二条语句控制误报：如果两个向量不相似并且它们之间的距离大于d2 ，则它们出现在同一桶中的概率上限为p2阈值。

考虑到上面的陈述，我们通常希望系统中满足以下陈述：

p₁应尽可能接近 1，以减少假阴性的数量。
p2应尽可能接近 0，以减少误报的数量。
d₁和d2之间的差距应尽可能小，以减少无法对数据进行概率估计的区间。

左图显示了一条典型曲线，展示了 (d1, d2, p1, p2) 符号的 LSH 参数之间的关系。右侧的曲线展示了阈值d₁和d2之间没有间隙的理想情况。

有时，上面的陈述是通过使用相似度s而不是距离d 来引入的：

给定相似性度量 s，如果对于随机选择的对象 x 和 y，满足以下条件，则 H 被称为 (s₁, s2, p₁, p2) 敏感的 LSH 函数：

如果 s(x, y) ≥ s₁，则 p(H(x) = H(y)) ≥ p₁，即 H(x) = H(y) 的概率至少为 p₁。
如果 s(x, y) ≤ s2，则 p(H(x) = H(y)) ≤ p2，即 H(x) = H(y) 的概率至多为 p2。

左图显示了一条典型曲线，展示了 ( s1, s2, p1, p2 ) 符号的 LSH 参数之间的关系。右侧的曲线展示了阈值s₁和s2之间没有间隙的理想情况。

注意。在本文中，将使用两种符号（d1、d2、p1、p2）和（s1、s2、p1、p2）。根据文本中符号中使用的字母，应该清楚是暗示距离d还是相似度s 。默认情况下，使用符号(d₁, d2, p₁, p2) 。

三、LSH 示例

为了让事情更清楚，让我们证明以下陈述：

如果距离度量s是 Jaccard 指数，则H是一个(0.6, 0.6, 0.4, 0.4)敏感的 LSH 函数。基本上，必须证明等价的陈述：

如果 d(x, y) ≤ 0.6，则 p(H(x) = H(y)) ≥ 0.4
如果 d(x, y) ≥ 0.6，则 p(H(x) = H(y)) ≤ 0.4

从本系列文章的第 5 部分中，我们知道两个二进制向量获得相等哈希值的概率等于 Jaccard 相似度。因此，如果两个向量相似度至少为 40%，那么就保证获得相等哈希值的概率也至少为 40%。同时，至少 40% 的 Jaccard 相似度相当于最多 60% 的 Jaccard 指数。至此，第一个命题得证。对于第二个语句可以进行类似的思考。

这个例子可以推广为定理：

定理。如果 d 是杰卡德指数，则 H 是 LSH 函数的 (d₁, d2, 1 — d₁, 1 — d2) 族。

同样，根据第6部分得到的结果，可以证明另一个定理：

定理。如果 s 是余弦相似度（在 -1 和 1 之间），则 H 是 LSH 函数的 (s₁, s2, 1 — arccos(s₁) / 180, 1 — arccos(d2) / 180) 系列。

四、组合 LSH 函数

让我们参考一下之前在 LSH 中学到的有用概念：

回到关于 minhashing 的第 5 部分，每个向量都被分成几个带，每个带包含一组行。为了将一对向量视为候选向量，必须存在至少一个所有向量行都相等的带。
关于随机投影的第 6 部分，仅当存在至少一棵树且所有随机投影均未分离初始向量时，才将两个向量视为候选向量。

我们可以注意到，这两种方法在底层有相似的范例。仅当n 个配置向量中至少有一次k次具有相同的哈希值时，它们才将一对向量视为候选向量。使用布尔代数符号，可以写成这样：

基于这个例子，让我们介绍逻辑运算符OR和AND，它们允许聚合一组哈希函数。然后我们将估计它们如何影响两个候选向量的输出概率以及假阴性和假阳性错误率。

3.1 与运算符

给定 n 个独立的 LSH 函数 H₁、H2、…Hₙ，仅当两个向量的所有n 个对应哈希值都相等时， AND运算符才会将两个向量视为候选对。否则，向量不被视为候选向量。

如果通过AND运算符聚合两个高度不同的向量的哈希值，那么它们成为候选者的概率随着使用的哈希函数数量的增加而降低。因此，假阳性的数量减少了。

同时，两个相似的向量可能会偶然产生一对不同的哈希值。因此，算法不会认为此类向量相似。这方面导致假阴性率较高。

定理。考虑 r 独立 (s₁, s2, p₁, p2) 敏感的 LSH 函数。将这些 r LSH 函数与 AND 运算符组合会产生一个新的 LSH 函数，其参数为

使用几个独立事件的概率公式很容易证明这个说法，该公式乘以所有事件的概率来估计所有事件发生的概率。

2.2 或运算符

给定 n 个独立的 LSH 函数 H₁、H2、…Hₙ，仅当两个向量的 n 个对应哈希值中至少有一个相等时， OR运算符才会将两个向量视为候选对。否则，向量不被视为候选向量。

与AND运算符相反，OR运算符增加了任意两个向量成为候选向量的概率。对于任何向量对，至少有一个对应的哈希值相等就足够了。因此，OR 聚合会减少假阴性的数量并增加假阳性的数量。

定理。考虑b 个独立的 (d₁, d2, p₁, p2) 族 LSH 函数。将这b 个LSH 函数与 AND 运算符组合会产生一个新的 LSH 函数，其参数为

我们不会证明这个定理，因为本系列文章的第 5 部分已经获得并解释了由此产生的类似概率公式。

3.3 作品

通过AND和OR运算，可以通过各种方式将它们组合在一起，以更好地控制误报率和漏报率。让我们想象一下AND组合器使用r LSH 函数，OR组合器使用b LSH 函数。使用这些基本组合器可以构建两种不同的组合：

AND-OR 和 OR-AND 是可以使用 AND 和 OR 运算符构建的两种组合类型。

前两篇文章中描述的算法使用AND-OR组合。事实上，没有什么可以阻止我们基于AND和OR运算构建更复杂的组合。

3.4 构图示例

让我们研究一个示例，了解AND和OR的组合如何显着提高性能。假设参数b = 4和r = 8的OR-AND组合。根据上面的相应公式，我们可以估计两个候选向量在组合后的初始概率如何变化：

通过应用参数 b = 4 和 r = 8 的 OR-AND 组合来改变概率。第一行显示初始概率，第二行显示转换后的概率。

例如，如果对于两个向量之间的某个相似度值，单个 LSH 函数在 40% 的情况下将它们散列到同一个存储桶，那么在 OR- AND组合之后，在 32.9% 的情况下它们将被散列。

要了解组合的特殊之处，请考虑(0.4, 1.7, 0.8, 0.2)敏感的 LSH 函数。经过OR-AND转换后，LSH 函数转换为(0.4, 1.7, 0.0148, 0.987)敏感格式。

本质上，如果最初两个向量非常相似并且距离小于 0.4，那么在 80% 的情况下它们将被视为候选向量。然而，通过应用组合，它们现在是 98.7% 场景的候选者，从而导致假阴性错误大大减少！

类似地，如果两个向量彼此非常不同并且距离大于 1.7，那么现在仅在 1.48% 的情况下将它们视为候选向量（之前为 20%）。这样，误报错误的频率减少了 13.5 倍！这是一个巨大的进步！

显示不同组合后初始概率如何转换的曲线

一般来说，通过使用(d₁, d2, p₁, p2)敏感的 LSH 函数，可以将其转换为(d₁, d2, p'₁, p'2)格式，其中p'₁接近 1 p'2接近 0。越接近 1 和 0 通常需要使用更多的组合。

五、其他距离指标的 LSH

我们已经深入研究了 LSH 方案，用于保存有关 Jaccard 指数和余弦距离的信息。自然出现的问题是是否可以将 LSH 用于其他距离度量。不幸的是，对于大多数指标，没有相应的 LSH 算法。

然而，LSH 模式适用于欧几里得距离——机器学习中最常用的指标之一。由于它经常使用，我们将研究如何获取欧氏距离的哈希值。通过上面介绍的理论符号，我们将证明该指标的一个重要的 LSH 属性。

4.1 欧几里得距离的 LSH

欧几里得空间中点的散列机制包括将它们投影到随机线上。算法假设

如果两个点彼此相对接近，那么它们的投影也应该接近。
如果两点彼此相距很远，那么它们的投影也应该很远。

为了测量两个投影的接近程度，可以将一条线分为几个相等的段（桶），每个段的大小为a。每条线段对应一个特定的哈希值。如果两个点投影到同一条线段，则它们具有相同的哈希值。否则，哈希值是不同的。

在随机线上投影点

尽管该方法乍一看似乎很强大，但它仍然可以将彼此相距较远的点投影到同一段。当连接两点的线几乎垂直于初始投影线时，尤其会发生这种情况。

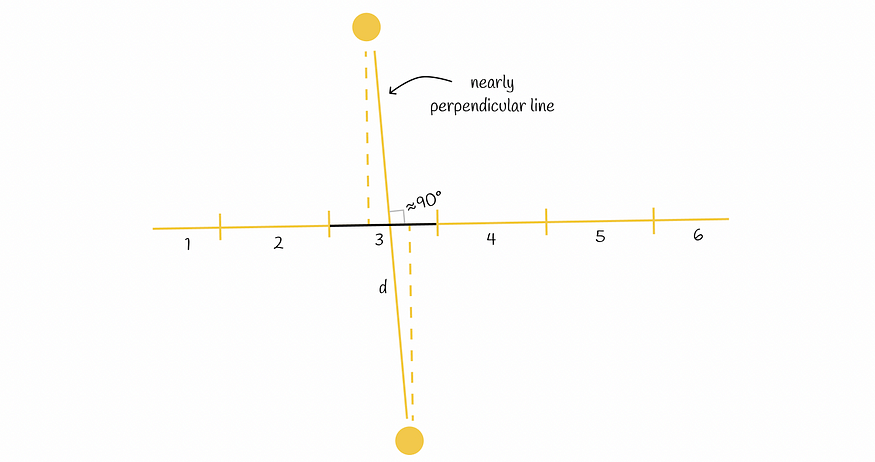
尽管两个点彼此相距较远，但它们仍然有可能被散列到同一个桶中。

为了降低错误率，强烈建议使用随机投影线的组合，如上所述。

几何上可以证明，如果a是欧氏空间中单条线段的长度，则H是(a/2,2a,1/2,1/3)敏感的LSH函数。

六、结论

在本章中，我们积累了一般 LSH 表示法的知识，这有助于我们正式引入组合操作，从而显着降低错误率。值得注意的是，LSH 仅适用于一小部分机器学习指标，但至少适用于最流行的指标，如欧氏距离、余弦距离和杰卡德指数。当处理测量向量之间相似性的另一个度量时，建议选择另一种相似性搜索方法。

作为参考，本文中介绍的陈述的正式证明可以在这些注释中找到。

七、资源

局部敏感哈希 | 大数据分析讲义| 尼姆拉·穆斯塔法
余弦距离 | 维基百科