目录
6.1 回溯法的设计技术 :
四皇后问题
回溯法:
算法框架:
思考题:
回溯算法的适用条件
【例6-1】求满足下列不等式的所有整数解:
6.2回溯算法的经典例题
【例6-2】装载问题
问题分析
计算模型
算法设计与描述
算法分析:
代码:
【例6-3】n皇后问题。
问题分析 算法思想详见开篇。
计算模型
算法设计与描述
算法分析
另一种:随机算法
【例6-4】 0-1背包问题。
问题分析
数学模型
计算模型
算法设计与描述
算法分析
代码:
【例6-5】旅行商问题(Traveling Salesman Problem,简称TSP)。
问题分析
计算模型
算法设计与描述:
小结
分支限界法的设计技术
分支限界法:
约束条件
剪枝
分支限界法的设计步骤
思考题:
【例6-6】装载问题。
计算模型
【例6-7】背包
问题分析
问题分析
计算模型
计算模型
算法设计与描述
【例6-8】旅行商问题(Traveling Salesman Problem,TSP):
问题分析
计算模型
算法设计与描述
6.1 回溯法的设计技术 :
回溯法:
算法框架:
| 回溯的递归框架 | 回溯的非递归模式 |
| 输入:n | |
| 输出:所有的解x[] | |
| int x[n],i=1; 输出结果; | int x[n],i=1; //还未回溯到头, i为真 表示有路可走 while(i&&(未达到目标) ) { if(i>n)//搜索到叶节点 搜索到一个解,输出; else//处理第i个元素 { x[i]第一个可能的值; //x[i]不满足约束条件,但在搜索空间内 while( !P(x[i]) && x[i]在搜索空间内 ) x[i]下一个可能的值; if( x[i]在搜索空间内) { 标识占用的资源; i=i+1;//扩展下一个结点 } else { 清理所占的状态空间; i=i-1;//回溯 } } } |
思考题1:

(1)不是唯一, n元组
(3)剪枝:判断是否满足约束条件。执行:将结点标为死结点。
回溯算法的适用条件
P(Xi+1) -> P(Xi) i∈(0,n) ,其中,n代表解向量的维数。
【例6-1】求满足下列不等式的所有整数解:
![]()

【丢解】
当x1=1、x2=2时, P(x1 ,x2 )= 5x1+4x2=5*1+4*2=13>10 不满足约束条件,分支x2=2将被剪去
【解决】
如果令x’3=4-x3 ,将原不等式变换为:5x1+4x2+x’3≤14 1≤xi , x’3≤3 i=1, 2
代码:
#include<iostream>
using namespace std;
//
int n=3;
int x[3]={1,1,1};
void show(int a[])
{
for(int i=0;i<n;i++)
cout<<a[i]<<"\t";
cout<<endl<<endl;
}
//约束条件
bool P(int x[],int i)//表示第几层
{
switch(i)
{
case 0:
if(5*x[0]<=14)return true;
else return false;
case 1:
if(5*x[0]+4*x[1]<=14)return true;
else return false;
case 2:
if(5*x[0]+4*x[1]+x[2]<=14)return true;
else return false;
}
}
void fun(int i)
{
// cout<<i<<"c"<<endl;
// show(x);
if(i>n-1)//已经结束了最后一个数
{
// cout<<"结果:";
show(x);
return;//结束最后一层,回溯到上一层
}
//若不变
if(P(x,i)&&x[i]<4)//符合约束条件
{
x[i]=1;
fun(i+1); //下一层
}
//若2
if(P(x,i)&&x[i]<4)//符合约束条件
{
int t=x[i];
x[i]=2;
fun(i+1); //下一层
x[i]=t;//回复
}
//若3
if(P(x,i)&&x[i]<4)//符合约束条件
{
int t=x[i];
x[i]=3;
fun(i+1); //下一层
x[i]=t;//回溯后,本层尝试下一个可能
}
}
int main()
{
fun(0);
return 0;
}
/*
1 1 1
1 1 2
1 1 3
1 2 1
1 2 2
1 2 3
*/6.2回溯算法的经典例题
【例6-2】装载问题
问题分析


其中,wi 表示第i个集装箱的重量。

计算模型
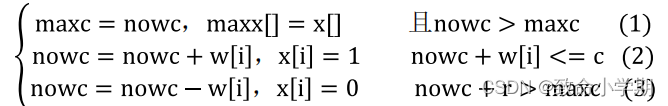
算法设计与描述
void search (int i){ /*递归法*/
if(i>n){//搜索完
if(nowc>maxc){//现在重量值
maxc=nowc;
for(int j=1;j<=n;j++)
maxx[j]=x[j];
}
return;
}
//剩余量
r=r-w[i]; //搜索第i层,同时减少可用量
//若不装,则岸上重量减去
if(nowc+w[i]<=c){ //满足约束,左子树
x[i]=1;
nowc=nowc+w[i];
search(i+1);//递归搜索i+1层
nowc=nowc-w[i];//回溯后恢复nowc
}
/*下面开始搜索右子树*/
if(nowc+r>maxc){ /*大于当前最优*/
x[i]=0;
search(i+1); //递归搜索i+1层
}
r=r+w[i];//对第i层搜索完毕,恢复r
}
算法分析:
代码:
#include<iostream>
using namespace std;
int n=5;//集装箱数量
int c=10;//轮船载重
int w[]={7,2,6,5,4};//集装箱的重量
int nowc=0;//当前载重量
int x[5];//当前解
int maxc=0;//当前最优重量
int maxx[5]; //当前最优解
int r=7+2+6+5+4;//剩余集装箱的总重量
void show(int a[])
{
for(int i=0;i<n;i++)
cout<<a[i]<<"\t";
cout<<endl<<endl;
}
void search (int i){ /*递归法*/
if(i>n-1){//搜索完 递归出口
if(nowc>maxc){//现在重量值>当前最优
//更新最优解
maxc=nowc;
//记录最优解的路径
for(int j=1;j<=n;j++)
maxx[j]=x[j];
}
return;//结束最后一层的函数,回溯到上一层进行递归调用
}
r=r-w[i]; //此时 陆地上集装箱的剩余重量
//若不装,则岸上重量减去
if(nowc+w[i]<=c){ //满足约束(小于轮船载重量),左子树
x[i]=1;
nowc=nowc+w[i];
search(i+1);//递归搜索i+1层
nowc=nowc-w[i];//回溯后恢复nowc
//回到上一层
}
/*下面开始搜索右子树 */
//右子树是否需要递归
if(nowc+r>maxc){ /*上界函数 此时当前轮船已载重量+剩余集装箱重量 > 当前最优*/
x[i]=0;
search(i+1); //递归搜索i+1层
}//否则不进行递归,也就是可以确认为死结点
r=r+w[i];//对第i层搜索完毕,恢复r
//陆地上增加
}
int main()
{
search(0);//从第1层开始
cout<<maxc<<endl;
show(maxx);
return 0;
}【例6-3】n皇后问题。
问题分析 算法思想详见开篇。
计算模型
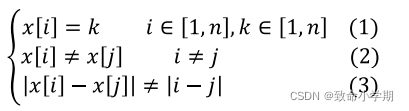
其中,式(2)与式(3)共同构成了对式(1)中所取得的值的一个评价,所以可以统称式(2)和式(3)为评价函数P。
算法设计与描述
/*判断当前格局x[1...i],是否符合约束*/
bool ok(int i){
for(int j=1;j<i;j++)
//值相等 或 在对角线上
if(x[i]==x[j]||(abs(x[i]-x[j])==(i-j)))
return false;
return true;
}
void queen(int i){
if(i>n){//找到可行解
for(int j=1;j<=n;j++)
printf("%-5d",x[j]);
printf("\n");
sum=sum+1;//可行解数目+1
}
for(int j=1;j<=n;j++){//每一层都有n个元素
x[i]=j;
if(ok(i))//如果满足约束
queen(i+1);//搜索第i+1层
//否则就结束在这一层
}
} 算法分析
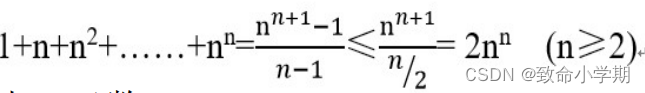
另一种:随机算法
【例6-4】 0-1背包问题。
问题分析
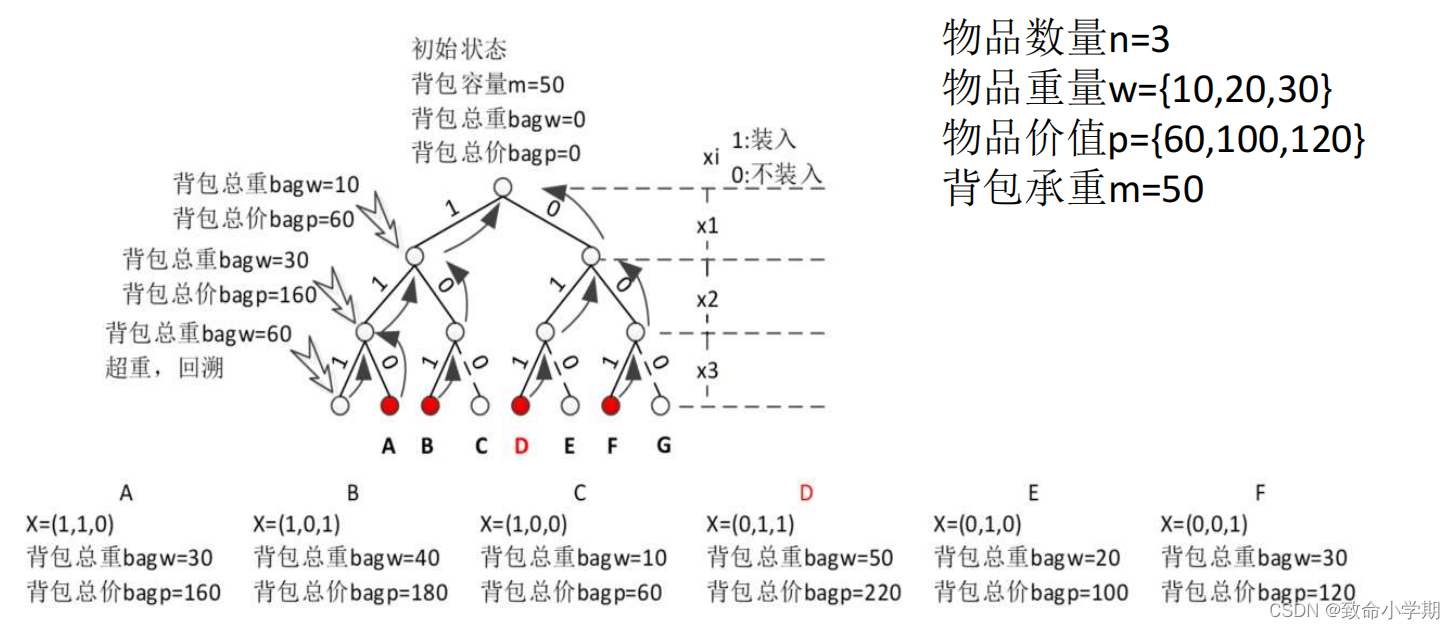
数学模型
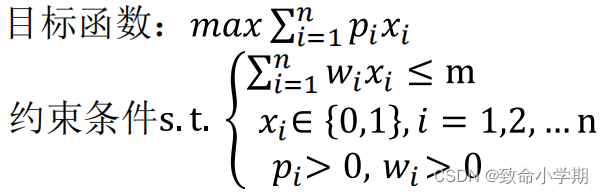
pi第i个物品价值>0,xi第i个物品是否被选择[0,1]
计算模型
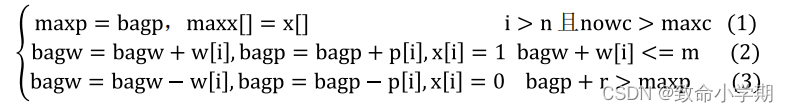
算法设计与描述
算法分析

思考题:

| 蛮力法 | 回溯法 | |
| 区别 | 回溯法有对右子树的剪枝 | |
| 时间渐进复杂度 | T(n)=O(2^n) | T(n)=O(2^n) |
| 区别 | 在实际运算中,同样情况下回溯法的时间复杂度优于蛮力法,回溯法最坏情况下的时间渐进复杂度与蛮力法相同。 | |
| 原因 | 回溯法存在剪枝操作。 | |
代码:
#include<iostream>
using namespace std;
int n=3;//物品数量
int w[]={10,20,30};//物品重量
int p[]={60,100,120};//物品价值
int m=50;//背包称重
//使物品总价值最大
int bagw=0;//当前背包重量
int bagp=0;//当前背包价值
int x[3];//当前最优解
int maxp=0;//当前最优总价值
int maxx[3];//最优解
int r=60+100+120;//可用的物品价值,也就是物品总价值剩余量
void show(int a[])
{
for(int i=0;i<n;i++)
cout<<a[i]<<"\t";
cout<<endl<<endl;
}
void bag(int i)
{
if(i>n-1)
{
if(bagp>maxp)
{
maxp=bagp;
for(int j=0;j<n;j++)
{
maxx[j]=x[j];
}
}
return ;
}
//
r=r-p[i];//对第i层进行搜索,r 减少
if(bagw+w[i]<=m)//小于背包总重量(约束条件)
{
x[i]=1;
bagw=bagw+w[i];//更新当前背包重量
bagp=bagp+p[i];//更新价值
bag(i+1);//下一层
bagw=bagw-w[i];//回溯
bagp=bagp-p[i];
}
if(bagp+r >maxp)//如果当前价值+剩余价值> 当前最大价值 还有递归的必要
//如果是 当前价值+剩余价值 <= 当前最大价值,那么其实就没有递归的必要了
{
x[i]=0;//右子树
bag(i+1);
}
r=r+p[i];//对第i层进行搜索回来,回复r
}
int main()
{
bag(0);
cout<<maxp<<endl;
show(maxx);
return 0;
}【例6-5】旅行商问题(Traveling Salesman Problem,简称TSP)。

问题分析
计算模型
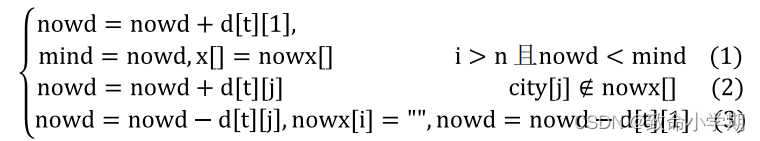
算法设计与描述:


| 蛮力法 | 回溯法 | |
| 区别 | ||
| 时间渐进复杂度 | O( (n-1)! ) | O( (n-1)! ) |