一、什么是逻辑回归
1、逻辑回归(Logistic Regression)是机器学习中的一种分类模型,逻辑回归是一种分类算法,虽然名字中带有回归,但是它与回归之间有一定的联系。由于算法的简单和高效,在实际中应用非常广泛
2、叫回归,但是它是一个分类算法
二、逻辑回归的应用场景
1、应用场景
广告点击率:预测是否会被点击
是否为垃圾邮件
是否患病
金融诈骗:是否为金融诈骗
虚假账号:是否为虚假账号
均为二元问题
2、看到上面的例子,我们可以发现其中的特点,那就是都属于两个类别之间的判断。逻辑回归就是解决二分类问题的利器
会有一个正例,和一个反例
三、逻辑回归的原理
1、逻辑回归的输入
线性回归的输出,就是逻辑回归的输入![]()
逻辑回归的输入就是一个线性回归的结果
2、怎么用输入来分类
要进行下一步处理,带入到sigmoid函数当中,我们把它叫做激活函数
3、sigmoid函数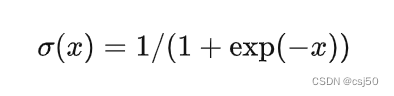
可以理解为,f(x)=1/(1+e^(-x)),1加上e的负x次方分之1
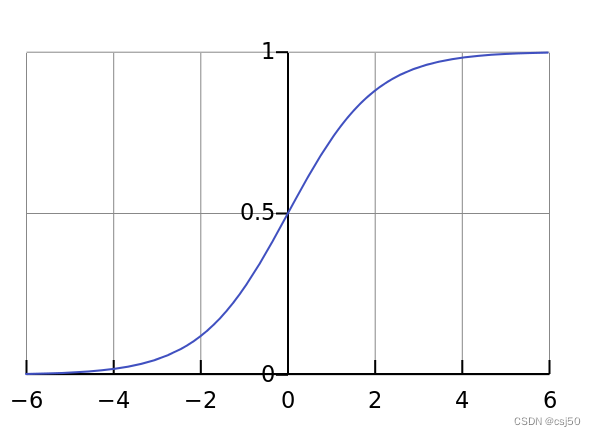
sigmoid函数又称S型函数,它是一种非线性函数,可以将任意实数值映射到0-1之间的值,通常用于分类问题。它的表达式为:f(x)=1/(1+e^(-x)),其中e为自然对数的底数。它的输出值均位于0~1之间,当x趋向正无穷时,f(x)趋向1;当x趋向负无穷时,f(x)趋向0
4、分析
将线性回归的输出结果,代入到x的部分
输出结果:[0, 1]区间中的一个概率值,默认为0.5为阈值
逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别,并且这个类别默认标记为1(正例),另外的一个类别会标记为0(反例)。(方便损失计算)
5、假设函数/线性模型
1/(1 + e^(-(w1x1 + w2x2 + w3x3 + ... + wnxn +b)))
如何得出权重和偏置,使得这个模型可以准确的进行分类预测呢?
6、损失函数(真实值和预测值之间的差距)
我们可以用求线性回归的模型参数的方法,来构建一个损失函数
线性回归的损失函数:(y_predict - y_true)平方和/总数,它是一个值
而逻辑回归的真实值和预测值,是否属于某个类别
所以就不能用均方误差和最小二乘法来构建
要使用对数似然损失
7、优化损失(正规方程和梯度下降)
用一种优化方法,将损失函数取得最小值,所对应的权重值就是我们求的模型参数
四、对数似然损失
1、公式
逻辑回归的损失,称之为对数似然损失
(1)它是一个分段函数
(2)如果y=1,真实值是1,属于这个类别,损失就是 -log(y的预测值)
(3)如果y=0,真实值是0,不属于这个类别,损失就是 -log(1-y的预测值)
2、怎么理解单个的式子呢?这个要根据log的函数图像来理解
当y=1时:(横坐标是y的预测值)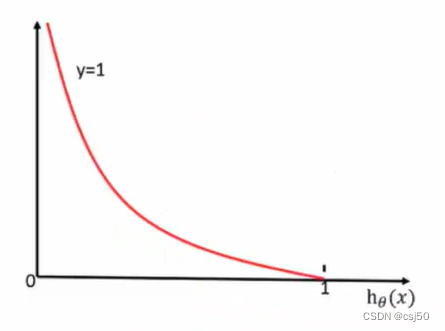
前提真实值是1,如果预测值越接近于1,则损失越接近0。如果预测值越接近于0,则损失越大
当y=0时:(横坐标是y的预测值)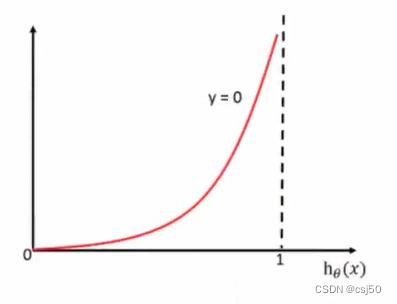
前提真实值是0,如果预测值越接近1,则损失越大
3、综合完整损失函数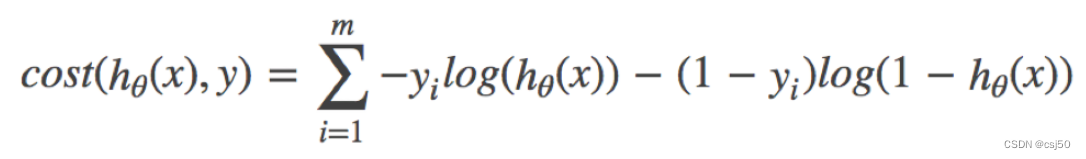
损失函数:-(y真实*logy预测+(1-y真实)*log(1-y预测)),求和
![]() 是线性回归的输出,经过sigmoid函数映射之后的一个概率值
是线性回归的输出,经过sigmoid函数映射之后的一个概率值
4、计算样例
五、优化损失
同样使用梯度下降优化算法,去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数,提升原本属于1类别的概率,降低原本是0类别的概率
六、逻辑回归API
1、sklearn.linear_model.LogisticRegression(solver='liblinear', penalty='l2', C=1.0)
solver:优化求解方式(默认开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数)
auto:根据数据集自动选择,随机平均梯度下降
penalty:正则化的种类
C:正则化力度
2、LogisticRegression方法相当于SGDClassifier(loss="log", penalty=" ")
SGDClassifier是一个分类器
SGDClassifier实现了一个普通的随机梯度下降学习,也支持平均随机梯度下降法(ASGD),可以通过设置average=True
而使用LogisticRegression它的优化器已经可以使用SAG