【算法设计与分析】第6章02 分支限界法

分支限界法的设计技术

分支限界法：

 约束条件

 剪枝

 分支限界法的设计步骤

思考题：

【例6-6】装载问题。

 计算模型

【例6-7】背包

 问题分析

计算模型

 计算模型

 算法设计与描述

代码：

思考：

【例6-8】旅行商问题(Traveling Salesman Problem，TSP)：

 问题分析

 计算模型

 算法设计与描述

分支限界法的设计技术

分支限界法（区别）：

限界值和上界函数

分支限界法：

增加约束条件，剪掉解空间中更多分支，加快算法的执行速度。

 约束条件

（1）上界函数：用来求得以当前结点为根的可行性解可能达到的极值【估测】。

（2）限界值：搜索到某一结点时，已经得到可行解或可能包含可行性解的最优值。

（3）评价函数：判定当前所获得路径或值是否为解的函数

 剪枝

（1）该结点的上界小于界限值，即再往下搜索也不可能有更优的值。【以该节点为根的子树】

（2）该结点无法代表任何可行解，因为它已经违反了问题的约束，不能满足评价函数。

（3）该节点代表的可行解的子集只包含一个单独的点。

 分支限界法的设计步骤

（1）建立上界函数，函数值是以该结点为根的搜索树中的所有可行解在目标函数上求得值的上/下界。【不通过搜索来判断,一个估计】

（2）求得限界值，即当前巳经得到的可行解的目标函数的最大值。

（3）依据剪枝条件，停止分支的搜索，向上回溯到父结点。

（4）限界值的更新：当得到的可行解的目标函数值大于/小于当前限界值时，更新之。

思考题：

回溯：评价函数，即当前路径或值是否为解。

分支限界：上界函数，界限值，评价函数。

【例6-6】装载问题。

有n个集装箱要装上一艘载重量为c的

轮船，其中集装箱i的重量为wi 。在装载体积不受限制的情

况下，找出一种最优装载方案，将轮船尽可能地装满。

问题分析：

实例：船的载重量c=10，4个集装箱，重量W={7,4,2,6}。

c：船的载重量。 x[]：左儿子标识。

w[]：集装箱重量。 s：剩余总重量。

lw：已装船总重量。

bestw：当前装船最优值，限界值。

pw：预装重量，pw=lw+w[i]

评价函数：预装集装箱重量+已装重量<=船的载重 lw+w[i]<=c

上界函数：剩余重量+已装重量>限界值 s+lw > bestw

【深度遍历】如果左子树能装，就一直装，不考虑右子树

【限界】类似广度优先，必然要分层，引入队列

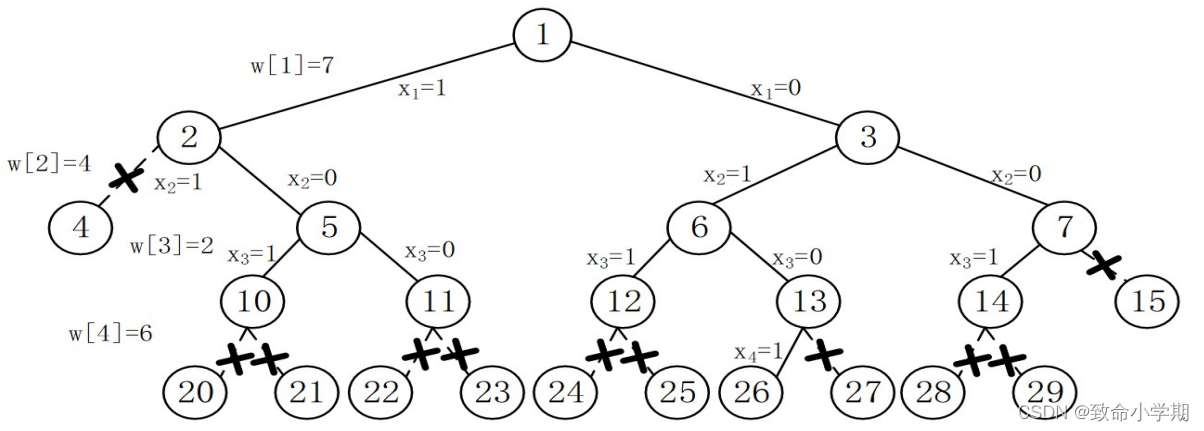
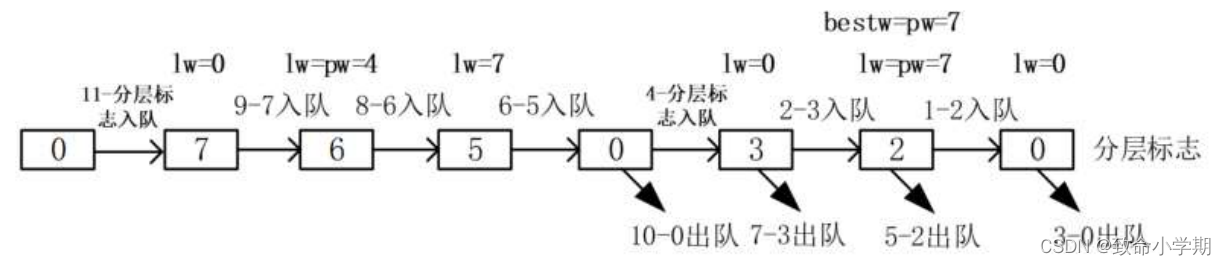
评价函数：lw+w[i]<c 上界函数：s+lw > bestw

 计算模型

结点的构造如下：

class QNode
{
	template<class T>
		friend int EnQueue(Queue<QNode<T>*>&Q, T wt, int i, int n,
			T bestw, QNode<T>*E, QNode<T>*&bestE, int bestx[], bool ch);
	template<class T>
		friend Type MaxLoading(Type w[],Type c, int n, int bestx[]);
public:
	QNode *parent; //父结点
	bool LChild; //左孩子标志，是左孩子值为真，否则为右孩子。
	Type weight; //结点权值
};

 算法设计与描述

//入队操作
int EnQueue(Queue<QNode<Type>*>&Q,Type pw,int i, int n, Type bestw, QNode<Type>*E,QNode<Type>*&bestE,int bestv[], bool x)
{ 
	if(i==n){//到达叶结点
		if (pw==bestw) {//找到最优值
			bestE=E;
			bestv[n]=x;
		}
	return 1; 
	}
	QNode<Type> *b;
	b=new QNode<Type>;
	b->weight=pw;
	b->parent=E;
	b->LChild=x;
	Q.Add(b);
	return 1;	
}


int main(int argc, const char * argv[]) {
	float c=10;
	float w[]={0,7,4,2,6};//7，4，2，6
	int x[N+1];
	float bestw;
	bestw=MaxLoading(w,c,N,x);
	
	cout<<"result is: "<<endl;
	for(int i=1;i<=N;i++)
		cout<<x[i]<<" ";
	cout<<endl;
	
	cout<<"best weight s:"<<bestw<<endl;
	return 0;
}

template<class Type>
Type MaxLoading(Type w[],Type c, int n, int bestv[])
{ 
	Queue<QNode<Type>*> Q;
	Q.Add(0);
	int i=1;
	Type lw=0,bestw=0,s=0;
	for(int j=2;j<=n;j++) 
		s+=w[j];
	QNode<Type> *E=0, *bestE;
	while(true)
	{ 
		Type pw=lw +w[i];//预装重量
		if(pw<=c)
		{ 
			if(pw>bestw) 
				bestw=pw; //选择集装箱
			EnQueue(Q,pw,i,n,bestw,E,bestE,bestv,true);
		}
		if(lw+s>bestw){//剪枝
			EnQueue(Q,lw,i,n,bestw,E,bestE,bestv,false);
		}//从队列Q中输出一个结点
		Q.Delete(E);
		if(!E) {
			if(Q.IsEmpty())
			break;
			Q.Add(0); //加入分层结点
			Q.Delete(E);
			i++;
			s-=w[i];
		}
		lw =E->weight;
	}
	for(int j=n-1;j>0;j--)
	{
		bestv[j] =bestE->LChild;
		bestE =bestE->parent;
	}
	return bestw;	
}

【例6-7】背包

已知有n件物品，物品i的重量为wi 、价值为pi ，此物品可以有

多个。现从中选取一部分物品装入一个背包内，背包最多可容纳的总重

量是m，如何选择才能使得物品的总价值最大。为了追求价值最大化，

同一物品可以装多件。

 问题分析

实例：背包总承重为10

（1）允许同一物品装载多个，非0-1背包问题。

（2）背包总承重10，最多可以装载5个A，3个B，2个C个，1个D。

（3）按每个物品单位重量的价值（vi /wi ）从大到小排列，得到如下表达式：

其中，x1 代表D的数量，x2 代表物品C，x3 代表物品B的数量，x4 代表物品A的数量。

 问题分析

（4）搜索到(x1 , x2 ,…, xk)结点时的上界用下列函数求得：

（5）剪支

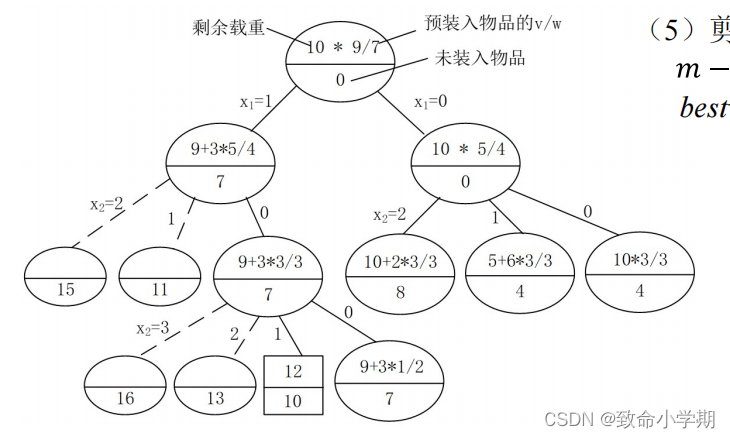
计算模型

（1）数据结构

 背包容量BTotal=m，物品品种数量n，选择树的层数为level。物品的特

征：

typedef struct{
	char name;//物品名称
	float v;//商品价值
	float w;//商品重量
	float key;// v/w
}goods;

物品：goods g[]

 当前背包所装物品重量bagW；当前背包所装物品总价bagP；

当前装载物品bagG[]，下标表示物品编号，值表示物品数量；

当前最优总价值bestV，当前最优解bestS[]，当前分支的上界ULimit。

 计算模型

（2）递归出口

（3）迭代公式

其中，i表示第level种物品装入的数量，i∈[0,BTotal/g[level].w]，。

回溯时需要恢复现场，所需要的迭代公式如下，

bagW=bagW-i*g[level].w;

bagP=bagP-i*g[level].v;

bagG[level]=0;

 算法设计与描述

输入：品种数量N；背包容量BTotal；物品描述

输出：最优总价值bestV和最优解bestS[]

knapsack(int level) //深入的层数
{ 
	int i,maxG;
	float ULimit=0;
	int j=0;
	if(level > n){
		if(bagP>bestV){
			for(i=0;i<n;i++)
				bestS[i]=bagG[i];
			bestV=bagP;
		}
		return;	
	}
	maxG=BTotal/g[level].w;
	ULimit=bagP+(BTotal-bagW)*g[level].key;

	if(bestV>=ULimit) return;//剪枝
	for(i=maxG;i>=0;i--)
	{ 
		if(bagW+i*g[level].w<=BTotal)
		{ 	
			bagW=bagW+i*g[level].w;
			bagP=bagP+i*g[level].v;
			bagG[level]=i;
			j=level;
			if(bagW==BTotal)//背包已装满
				for(j=j+1;j<n;j++) 
					bagG[j]=0;
			knapsack(j+1);
			bagW=bagW-i*g[level].w;
			bagP=bagP-i*g[level].v;
			bagG[level]=0;
		} 
	}
}

代码：

#include<bits/stdc++.h>
using namespace std;
//例6-7
//每种物品多个，求最大价值 
//深度优先搜索 

//数据结构
typedef struct{
	char name;//物品名称
	float v;//价值
	float w;//重量
	float key;//单位重量的价值 v/w 
}goods;

const int n=4;
goods g[n];



float bagW=0;//当前所装重量
float BTotal=10;//剩余总重量 

float bagP=0;//当前总价值
int bagG[n]={0};//下标表示物品编号，值表示物品数量；
float bestV=0;//当前最优总价值，
int bestS[n];//当前最优解，
float ULimit=0;//当前分支的上界。

void knapsack(int level) //深入的层数
{
	int i,j=0,maxG;
	float Ulimit=0;
	if(level>n)//递归出口 
	{
		if(bagP> bestV)//大有原最优 
		{//更新 
			for(int i=0;i<n;i++)
			{
				bestS[i]=bagG[i];
			}
			bestV=bagP;//最优价值 
		} 
		return; 
	}
	//
	maxG=BTotal/g[level].w;//整数 可能最大数目 
	//上界 
	ULimit=bagP+(BTotal-bagW)*g[level].key;
	//已装载价值 + （剩余容量）*当前最大单位价值 
	if(bestV>=ULimit)return;//剪去这枝 
	
	for(i=maxG;i>=0;i--)
	{
		if(bagW+i*g[level].w <=BTotal )
		{
			bagW += i*g[level].w;
			bagP+=i*g[level].v;
			bagG[level]=i;//所装数目
			
			j=level;
			
			if(bagW==BTotal)//背包满 
			{
				for(j++;j<n;j++)
				{
					bagG[j]=0;//之后都不装 
				 }
			} 
			//递归 下一层
			knapsack(j+1);
			//回溯 恢复现场 
			bagW -= i*g[level].w;
			bagP-=i*g[level].v;
			bagG[level]=0;//所装数目
			
		}
	}
	
}




int main()
{
	g[0].name='A';
	g[0].w=2;
	g[0].v=1;
	
	g[1].name='B';
	g[1].w=3;
	g[1].v=3;
	
	g[2].name='C';
	g[2].w=4;
	g[2].v=5;
	
	g[3].name='D';
	g[3].w=7;
	g[3].v=9;
	
	for(int i=0;i<n;i++)
		g[i].key= 1.0*g[i].v/g[i].w; 
	//按单位价值排序 从大到小
	for(int i=0;i<n-1;i++)
	{
		for(int j=0;j<i;j++)
			if(g[j].key < g[j+1].key )
			{
				char tname=g[j].name;
				g[j].name=g[j+1].name;
				g[j+1].name=tname;
				float t=g[j].v;
				g[j].v=g[j+1].v;
				g[j+1].v=t;
				t=g[j].w;
				g[j].w=g[j+1].w;
				g[j+1].w=t;
				t=g[j].key;
				g[j].key =g[j+1].key ;
				g[j+1].key =t;
			}
	} 
	for(int i=0;i<n;i++)
	{
		cout<<g[i].name<<endl;
	}
	knapsack(0);
	cout<<bestV<<endl;
	for(int i=0;i<n;i++)
	{
		cout<<g[i].name <<":"<< bestS[i]<<endl;
	}
	return 0;
} 
/*
11
B:2
C:1
A:0
D:0
*/

思考：

【例6-8】旅行商问题(Traveling Salesman Problem，TSP)：

有若干个城市，任何两个城市之间的距离都是确定的，现要求一旅行商从某城市

出发，必须经过每一个城市且只能在每个城市逗留一次，最后回到原出

发城市，问事先如何确定好一条最短的路线使其旅行的费用最少。

 问题分析

以有5个城市的旅行商问题为例，用分支限界法求解问题，如图所示。

（1）上界：

起点到终点一直是取当前最短边，终点回到起点的边长度不可确定，因此是一个比较好的解。

（2）下界：

每一个点都设一条出边，一条入边。

每个顶点入边最小值和入边最小值加起来，再除以2 ，就得到一个理想化的下界。

(3) 界函数

①将走过的路径和节点看成一个带权值的结点A【A-B的路径看成新的结点A'】，加入到图中，取代原来的结点与线段，构成新图，并且将后加入的结N点作为S的带权结点的离开结点，N引领的分支被称为离开分支；【比如此时 B邻接顶点中-C最短，离开结点就是C，而回到A也是C最短，进入结点也是C，进入边也就找到了】

②利用（2）中的方法，计算新图的low值，称为离开分支的lb (low bound)。

计算方法如下

lb=( (已经历路程)*2+新结点的进入边长度 +新结点离开边长度+其它每个结点的两个最短边长度)/2

其中，新结点的进入边是以起始结点为终点的最短边，新结点的离开边是以最晚加入新结点的结点为起点的最短边。

显然，如果lb>up，则此分支中不可能有高于up的最优解，不用再对此分支进行遍历；

③当沿某一个分支执行到叶子结点时，得到一个新的解，如果此解小于up，则可以用此解取代up的值，作为新的上界。【更新up】

④ 算法的改进：考虑到分支的lb值越小越有可能得到问题的最优解，因而可以引进一种数据结构—优先级队列，它可以按关键字的大小排列，如按从小到大顺序，最小的结点放在队头，依次排列，关键字相等的按先进先出的次序排列。

引进优先级队列有两个好处：一是可以更快地找到问题当前的最优解，更早地更新up值，剪掉更多

的分支；二是当找到的解小于队首结点的lb时，则找到了本问题的最优解，可以终结算法。

为什么？

每一次运算都把最小值排在最前。

因为lb存的是所有分支的最小值，队首是lb的最小值，因此就是本问题的最优解。

设A是起始点，A入队。

【考察A的所有相邻节点】

(A,B).lb = (AB*2+BC离开边+进入边CA+(C的两条最短边CA+CE)+(D的两条最短边DC+DE)+(E的两条最短边EC+ED))/2

= (4*2+7+2+(2+3)+(5+4)+(3+4))/2=19 //小于UP值，AC可以入队

(A,C).lb = (AC*2+CE+BA+(BA+BC)+(DC+DE)+(EC+ED))/2

= (2*2+3+4+(4+7)+(5+4)+(3+4))/2=19 //小于UP，入队

(A,D).lb = (AD*2+DE+CA+(BA+BC)+(CA+CE)+(EC+ED))/2 = 21 //<=UP 入队

(A,E).lb = (AE*2+EC+CA+(BA+BC)+(CA+CE)+(DC+DE))/2 = 24 //> up = 21 没有意义，被剪去

入队之后【排队】

AB边出队

(A,B,C).lb=((AB+BC)*2+CE+DA+(DA+DE)+(EC+ED))/2+1=24【向上取整】

(A,B,D).lb=((AB+BD)*2 +CA+DE +(CA+CE)+(EC+ED))/2=21

(A,B,E).lb=((AB+BE)*2+CA+EC+(CA+CE)+(DC+DE))/2=24

AC出队

(A,C,B).lb=((AC+CB)*2+BD+DA+(DA+DE)+(EC+ED))/2=24

(A,C,D).lb=((AC+CD)*2+DE +BA +(BA+BC)+(EC+ED))/2=20

(A,C,E).lb=((AC+CE)*2+EA+BA+(BA+BC)+(DC+DE))/2=19

【ACE，ABD 入队最小值在队首】

【ACE出队】

(A,C,E,D).lb=((AC+CE+ED)*2+DB+BA+(BA+BC))/2=21

(A,C,E,B).lb=((AC+CE+EB)*2+BD +DA+(EC+ED))/2=27

【此时ACDE只差一个顶点】

【ACD出队】

【AD出队】

(A,D,B).lb=((AD+DB)*2+BC+CA+(CA+CE)+(EC+ED))/2=25

(A,D,C).lb=((AD+DC)*2+CE +BA +(BA+BC)+(EC+ED))/2=24

(A,D,E).lb=((AD+DE)*2+EC+CA+(BA+BC)+(CA+CE))/2=21

【ABD出队】

(A,B,D, C).lb=((AB+BD+DC)*2+CE+EA+(EC+ED))/2=27

(A,B,D, E).lb=((AB+BD+DE)*2+EC +CA+(CA+CE))/2=21

(A,C,E,D,B,A)=AC+CE+ED+DB+BA=21

 计算模型

（1）所需要的数据结构

const int INF=10000000; //无穷大，表示两结点间没有直达的边

结点个数：n

上界与下界：low, up

不同城市之间线路的代价（权值）cost[][]、城市信息city[]

一个优先级队列q，并提供如下的结点信息：

struct node
{
	int st; //路径的起点
	int ed; //离开结点，当前路径的终点
	int k; //走过的结点数
	int sumv; //经过路径的总长度
	int lb; //每个分支的下界
	bool vis[]; //本路径中已经走过结点的标识
	int path[]; //记录经过的结点编号
};

（2）贪心算法初始化TSP问题的上界up

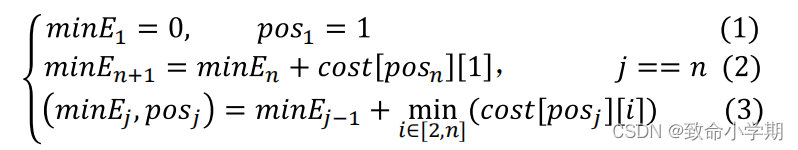
（3）求TSP问题的下界low

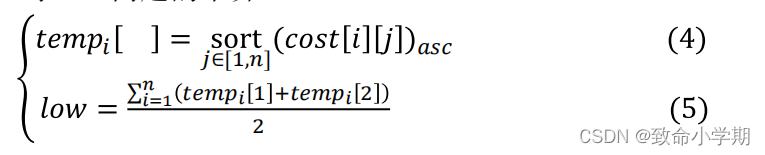
（4）每个分支的下界lb

（5）计算方法

① 计算up值。 ② 计算low值

③ 设置起始结点 start ，令 st=ed=start ， start.vis[1]=1, start.k=1, start.lb=low,

start.path[1]=1;

④ 按广度优先的方式逐步加入start临接点nexti，令ed=nexti，更新相关信息，计

算lb的值，若next.lb>up，则淘汰之（剪枝），否则加入队列，直到求出最优解

⑤ 当找到一个解时，用这个解的值与队首的lb值相比较，若此解小于或等于队

首的lb值，则意味着此解已是最优解，终止运算，输出结果。

 算法设计与描述

输入：城市数量n，距离矩阵cost[][]，城市名称city[]

输出：最优路径path[]，最优值mind

#include<iostream>

using namespace std;
//分支限界法
const int INF=10000000; //表示无穷大
int low, up, n, used[20], cost[20][20];
char city[20];

struct node
{ 
	bool vis[20];
	int st;//路径的起点
	int ed;//路径的终点
	int k;//走过的点数
	int sumv;//经过路径的距离
	int lb;//目标函数的值
	int path[20];
	//重载运算符”<”
	bool operator<(const node &p)const
	{ 
		return lb>p.lb; 
	} 
};

priority_queue<node> q; //优先级队列
struct node answer; //存储最优解变量

//用贪心算法和深度优先，求上界 
int get_up_helper(int v,int j,int len)
{ 
	int minE=INF,pos;
	if(j==n) return len+cost[v][1];
	
	for(int i=1;i<=n;i++)//当前结点的最小邻接边 
	{ //采用贪心算法取权值最小的边
		if(used[i]==0 && minlen>cost[v][i])
		{ 
			minE=cost[v][i]; 
			pos=i;//
		}
	}
	used[pos]=1;
	return get_up_helper(pos,j+1,len+minE);
} //这是一个深度优先算法

//求上界 
void get_up()
{ //user[]为结点状态伴随数组
	used[1]=1; //1表示已访问；0表示未访问
	up=get_up_helper(1,1,0);
}

//计算下界
void get_low()
{ 
	low=0;
	for(int i=1;i<=n;i++)//遍历每一个结点 
	{ 
		int temp[20];
		for(int j=1;j<=n;j++)//遍历 
		{ 
			temp[j]=cost[i][j]; 
		}
		sort(temp); 
//		sort(temp+1,temp+1+n);
		low = low+temp[1]+temp[2];//第一小 和 第二小 
	}
	low=low/2;
} //计算上界

//求由p引导的分支的下界
int get_lb(node p)
{ 
	int ret=p.sumv*2; //已遍历城市距离
	
	int min1=INF,min2=INF,pos;
	//最小入边 
	//从起点到最近未遍历城市的距离
	for(int i=1;i<=n;i++)
	{ 
		if(p.vis[i]==0&&min1>cost[p.st][i])
		{ 
			min1=cost[p.st][i]; 
			pos=i; 
		}
	}
	ret+=min1;
	//最小出边 
	//从离开结点到最近未遍历城市的距离
	for(int i=1;i<=n;i++)
	{ 
		if(p.vis[i]==0&&min2>cost[p.ed][i])
		{ 
			min2=cost[p.ed][i]; 
			pos=i; 
		}
	}
	ret+=min2;

	//进入并离开每个未遍历城市的最小成本
	for(int i=1;i<=n;i++)
	{ 
		if(p.vis[i]==0)
		{ 
			int temp[n];
			min1=min2=INF;
			for(int j=1;j<=n;j++)
			{ 
				temp[j]=cost[i][j]; 
			}	
			sort(temp+1,temp+1+n);
			ret+=temp[1]+temp[2];
		} 
	}
	//向上取整
	ret= ret%2==0?(ret/2):(ret/2+1);
	return ret;
}



int solve() //求解过程
{
	int ret=INF;
	get_up(); //求上界
	get_low();
	node start;
	start.st=1; start.ed=1; start.k=1;
	start.sumv=0; start.lb=low; 
	start.path[1]=1;
	for(int i=1;i<=n;i++)
	{ 
		start.vis[i]=0;
		start.path[i]=0;
	}
	
	start.vis[1]=1; 
	q.push(start);
	node next,temp;
	
	while(!q.empty())
	{ 
		temp=q.top(); 
		q.pop();
		//(1)如果只剩最后一个点了
		//不算出发顶点的倒数第二个 
		if(temp.k==n-1)
		{
			int pos=0;
			for(int i=1;i<=n;i++)
			{ 	
				if(temp.vis[i]==0)
				{ 
					pos=i; 
					break; 
				}
			}
			if(pos==0)
				break;
			//实际的值 
			int ans=temp.sumv+cost[pos][temp.st]+cost[temp.ed][pos];
			temp.path[n]=pos;//存最后一个结点
			temp.lb=ans;//更新结点的上界
			node judge=q.top();

			//(2)如果当前的路径和比所有分支
			//上界都小，则找到最优解
			if(ans<=judge.lb)
			{ 
				ret=min(ans,ret);
				answer=temp;//返回答案
				break;
			}
			//否则求其他可能的路径更新上界
			else if (up>=ans) 
			{ 
				up=ans;
				answer1=temp;
			}
			ret=min(ret,ans);
			continue;
		} 
	}
	//
	for(int i=1;i<=n;i++)
	{ 
		if(temp.vis[i]==0)//找到么有访问的相邻顶点 
		{ 
			//复制 刚才访问的起始点 
			next.st=temp.st;
			//在原来的距离 再加上 一个距离 
			next.sumv=temp.sumv	+cost[temp.ed][i];
			//记录一下最后 入列的这个顶点的编号 
			next.ed=i;
			//顶点数+1 
			next.k=temp.k+1;
			//记录该路径 编号 
			for(int j=1;j<=n;j++)
			{
				next.vis[j]=temp.vis[j];
				next.path[j]=temp.path[j];
			}
			//更新值 
			next.vis[i]=1;
			next.path[next.k]=i;//路径统计
			next.lb=get_lb(next);//新的下界 
			if(next.lb<=up) //否则剪枝
				q.push(next);
		} 
	}
	return ret;
}