---

一、Windows系统ftp服务器搭建

系统是2008r2，全图，按照图一步一步点就行了












找个有telnet的电脑测试一下端口，windows的ftp默认端口是21

返回是这个

同网段电脑登录测试

二、Linux系统ftp服务器搭建

Linux系统的话就更简单了，挂载镜像，配置yum源，直接rpm安装
如果不方便挂载镜像，安装包下载centos7包下载 centos6包下载

[root@hiscs ~]# cd /os
[root@hiscs os]# ls
CentOS_BuildTag  EFI  EULA  GPL  images  isolinux  LiveOS  Packages  repodata  RPM-GPG-KEY-CentOS-7  RPM-GPG-KEY-CentOS-Testing-7  TRANS.TBL
[root@hiscs os]# cd Packages/
[root@hiscs Packages]# ls *ftp*
ftp-0.17-67.el7.x86_64.rpm  lftp-4.4.8-8.el7_3.2.x86_64.rpm  tftp-5.2-13.el7.x86_64.rpm  tftp-server-5.2-13.el7.x86_64.rpm  vsftpd-3.0.2-22.el7.x86_64.rpm
[root@hiscs Packages]# rpm -ivh ftp-0.17-67.el7.x86_64.rpm 
warning: ftp-0.17-67.el7.x86_64.rpm: Header V3 RSA/SHA256 Signature, key ID f4a80eb5: NOKEY
Preparing...                          ################################# [100%]
	package ftp-0.17-67.el7.x86_64 is already installed

二、安装完成测试

1.测试将linux系统上的文件传输到windows服务器

[root@hiscs soft]# ftp
ftp> open 192.168.5.190 21   --win的端口号是21
Connected to 192.168.5.190 (192.168.5.190).
220 Microsoft FTP Service
Name (192.168.5.190:root): administrator  --输入win的用户名
331 Password required for administrator.
Password:   --输入win的密码
230 User logged in.
Remote system type is Windows_NT.
ftp> ls
227 Entering Passive Mode (192,168,5,190,254,12).
125 Data connection already open; Transfer starting.
10-18-23  03:54PM                    0 1.txt   --这样
226 Transfer complete.
ftp> lcd /home/soft    --本地系统切换到/home/soft目录
Local directory now /home/soft
ftp> mput ntp*     --传输文件测试
mput ntp-4.2.8p15? y
ntp-4.2.8p15: not a plain file.
mput ntp-4.2.8p15.tar.gz? y
227 Entering Passive Mode (192,168,5,190,254,13).
125 Data connection already open; Transfer starting.
226 Transfer complete.
7043140 bytes sent in 0.246 secs (28635.19 Kbytes/sec)

2.配置一个rman备份自动传输脚本

#!/bin/bash
export BACKUPTIME=`date +'%Y%m%d'`
export DELETETIME=`date -d -2day +%Y%m%d `
ftp -n >/backup/ftplog/toftp_full.log <<EOF
open 192.168.5.190 21
user administrator Ekinghis12#$
binary
hash
prompt
lcd /backup/file/$BACKUPTIME   --这个要配合rman备份脚本，在备份的时候自动生成以日期命名的文件夹
mput dbfull*
mput control*
mput arch*
mdelete dbfull*$DELETETIME.bak   --这个要配合rman备份脚本，在备份的时候自动生成以日期命名的文件
mdelete control*$DELETETIME.bak   --这个要配合rman备份脚本，在备份的时候自动生成以日期命名的文件
mdelete arch*$DELETETIME.bak   --这个要配合rman备份脚本，在备份的时候自动生成以日期命名的文件
close
bye
EOF

执行脚本，观察win系统ftp目录是否接收到文件

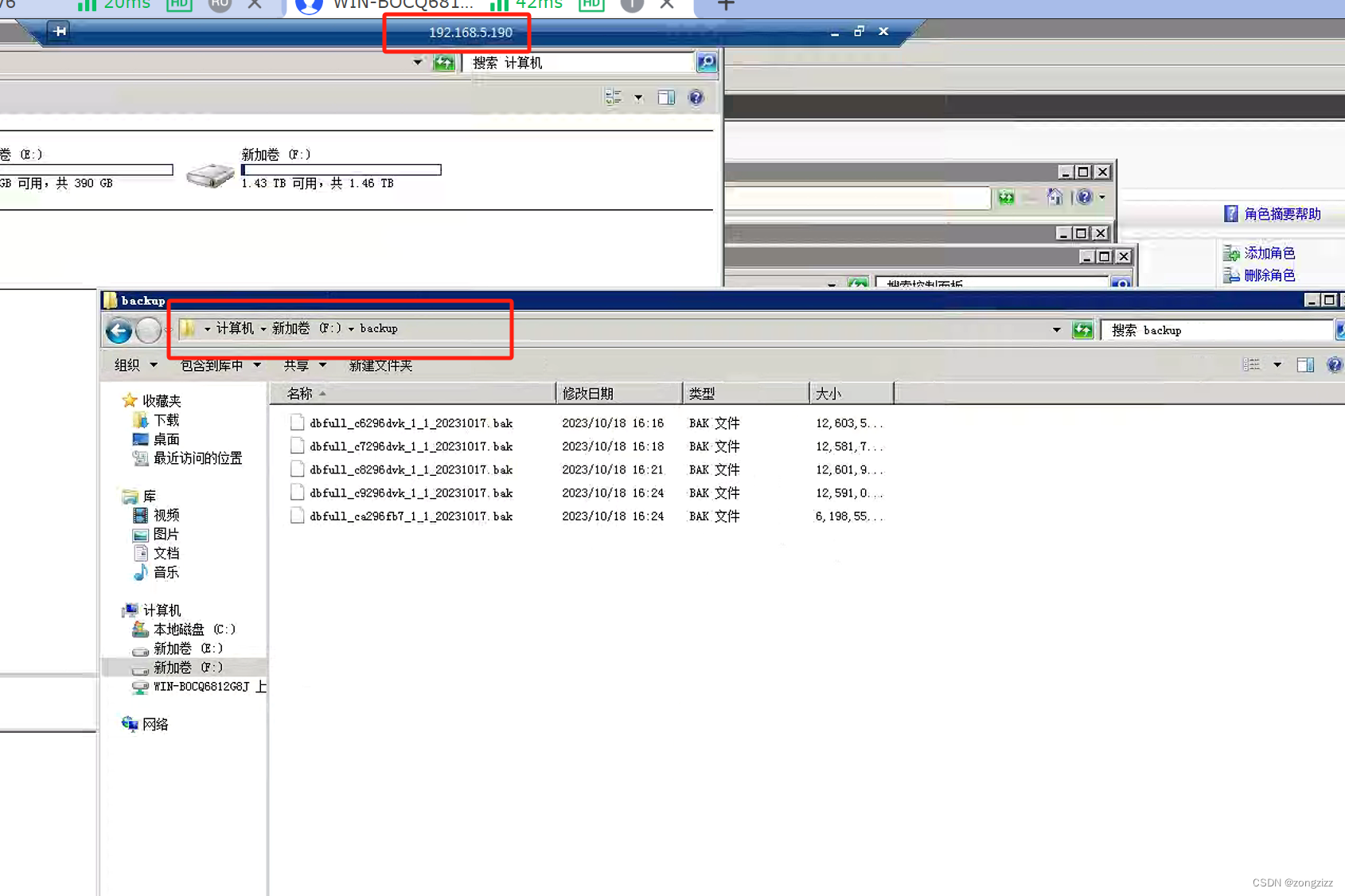
能正常接收，有需要的话可以配置定时任务，定时传输备份到异地服务器