---

前言

本文对雷达基础导论的内容以思维导图的形式呈现，有关仿真部分进行了讲解实现。

---

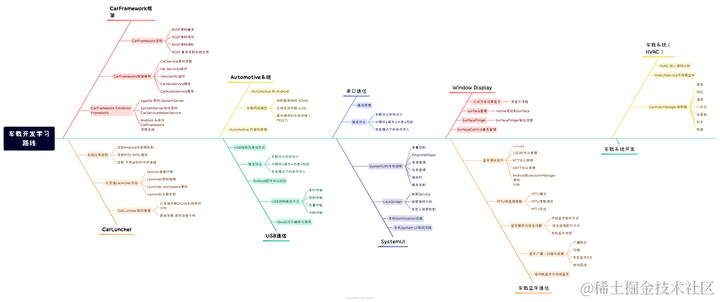
一、雷达基础导论

思维导图如下图所示，如有需求请到文章末尾端自取。

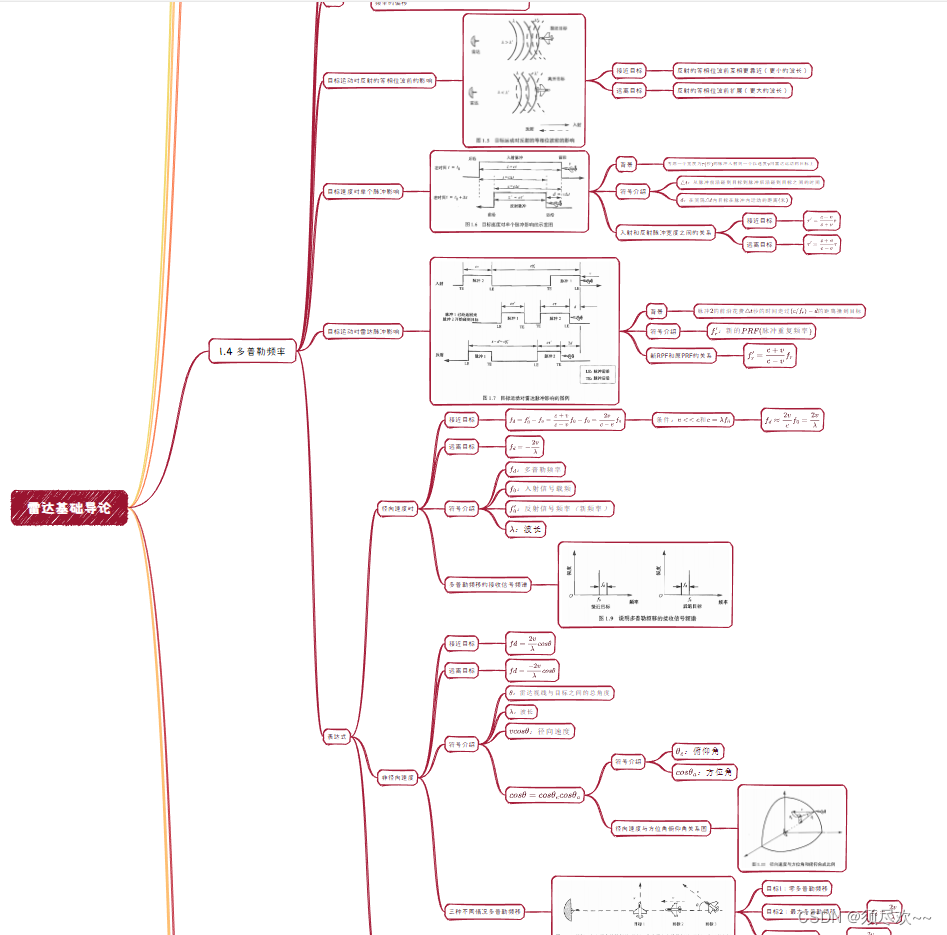
二、Matlab 仿真

1、SNR 相对检测距离的仿真

雷达方程：$$(SNR{)}_o=\frac{P_t{G}^2{\lambda }^2\sigma }{(4\pi {)}^{3}k{T}_{e}BFL{R}^4}$$

下面在三种不同数值的 RCS（雷达截面积）和三种不同数值的雷达峰值功率的情况下，对 SNR（信噪比） 相对检测距离的情况进行 Matlab 仿真

①、Matlab 源码

radar_eq.m

function [snr] = radar_eq(pt, freq, g, sigma, te, b, nf, loss, range)
% This program implements Eq. (1.56)
c = 3.0e+8; % speed of light
lambda = c / freq; % wavelength
p_peak = 10*log10(pt); % convert peak power to dB
lambda_sqdb = 10*log10(lambda^2); % compute wavelength square in dB
sigmadb = 10*log10(sigma); % convert sigma to dB
four_pi_cub = 10*log10((4.0 * pi)^3); % (4pi)^3 in dB
k_db = 10*log10(1.38e-23); % Boltzman's constant in dB
te_db = 10*log10(te); % noise temp. in dB
b_db = 10*log10(b); % bandwidth in dB
range_pwr4_db = 10*log10((range).^4); % vector of target range^4 in dB
% Implement Equation (1.56)
num = p_peak + g + g + lambda_sqdb + sigmadb;
den = four_pi_cub + k_db + te_db + b_db + nf + loss + range_pwr4_db;
snr = num - den;
return

相关参数说明：

符号	描述	单位	状态
pt	峰值功率	W	输入
freq	雷达中心频率	Hz	输入
g	天线增益	dB	输入
sigma	目标截面积	$m^2$	输入
te	有效噪声温度	K	输入
b	带宽	Hz	输入
nf	噪声系数	dB	输入
loss	雷达损失	dB	输入
range	目标距离（单位或矢量）	m	输入
snr	SNR(单值或矢量，根据输入距离)	dB	输出

函数 “radar.m” 的设计使它对于输入“距离”，可以接受单个数值，或包含很多距离值的矢量

fig1_12.m

close all
clear all
pt = 1.5e+6; % peak power in Watts
freq = 5.6e+9; % radar operating frequency in Hz
g = 45.0; % antenna gain in dB
sigma = 0.1; % radar cross section in m squared
te = 290.0; % effective noise temperature in Kelvins
b = 5.0e+6; % radar operating bandwidth in Hz
nf = 3.0; %noise figure in dB
loss = 6.0; % radar losses in dB
range = linspace(25e3,165e3,1000); % range to target from 25 Km 165 Km, 1000 points
snr1 = radar_eq(pt, freq, g, sigma, te, b, nf, loss, range);
snr2 = radar_eq(pt, freq, g, sigma/10, te, b, nf, loss, range);
snr3 = radar_eq(pt, freq, g, sigma*10, te, b, nf, loss, range);
% plot SNR versus range
figure(1)
rangekm  = range ./ 1000;
plot(rangekm,snr3,'k',rangekm,snr1,'k -.',rangekm,snr2,'k:')
grid
legend('\sigma = 0 dBsm','\sigma = -10dBsm','\sigma = -20 dBsm')
xlabel ('Detection range - Km');
ylabel ('SNR - dB');
snr1 = radar_eq(pt, freq, g, sigma, te, b, nf, loss, range);
snr2 = radar_eq(pt*.4, freq, g, sigma, te, b, nf, loss, range);
snr3 = radar_eq(pt*1.8, freq, g, sigma, te, b, nf, loss, range);
figure (2)
plot(rangekm,snr3,'k',rangekm,snr1,'k -.',rangekm,snr2,'k:')
grid
legend('Pt = 2.16 MW','Pt = 1.5 MW','Pt = 0.6 MW')
xlabel ('Detection range - Km');
ylabel ('SNR - dB');

②、仿真

仿真参数默认如下：
峰值功率 $P_t=1.5$ MW，工作频率 $f_0=5.6$ GHz，天线增益 $G=45$ dB，有效温度 $T_e=290$ K，雷达损失 $L=6$ dB，噪声系数 $F=3$ dB，雷达带宽 $B=5$ MHz，雷达最小和最大检测距离是 $R_{min}=25$ km 和 $R_{max}=165$ km，假定目标截面积 $\sigma =0.1$ $m^2$

1）、不同 RCS，SNR 相对检测距离仿真

对三种不同数值的 RCS，SNR 相对检测距离的曲线

注：分贝平方米（dBsm）：用雷达散射截面的对数值的十倍来表示，符号是σ dBsm，单位是分贝平方米（dBsm），即σ dBsm＝10lgσ。例如，RCS 值 0.1 平方米对应的是 －10 分贝平方米（即 －10dBsm）。

结论：从图中可以看到 RCS（雷达截面积）越大，雷达信噪比越大，且随着距离的增加，雷达信噪比逐渐减小；

2）、不同雷达峰值功率，SNR 相对检测距离仿真

对三种不同数值的雷达峰值功率，SNR 相对检测距离的曲线
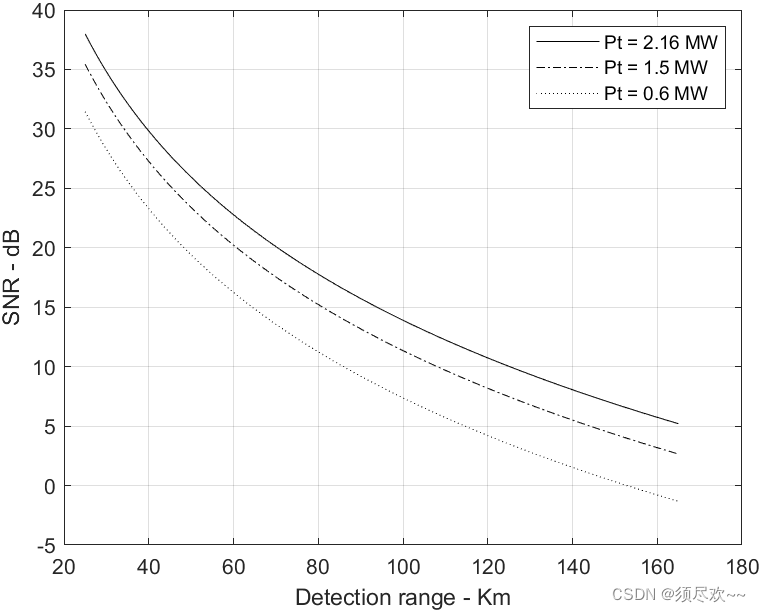
结论：从图中可以看到雷达峰值功率越大，雷达信噪比越大，且随着距离的增加，雷达信噪比逐渐减小

2、脉冲宽度相对所要求的 SNR 仿真

雷达检测门限：$$(SNR{)}_{o_{max}}=\frac{P_t{G}^2{\lambda }^2\sigma }{(4\pi {)}^{3}k{T}_{e}BFL{R}_{max}^4}$$

可以推出脉冲宽度 $$\tau =\frac{(4\pi {)}^{3}k{T}_{e}FL{R}^{4}SNR}{P_t{G}^2{\lambda }^2\sigma }$$

下面在三种不同的检测距离数值的情况下，对脉冲宽度相对所要求 SNR（信噪比）的情况进行 Matlab 仿真

①、Matlab 源码

fig1_13.m

close all
clear all
pt = 1.e+6; % peak power in Watts
freq = 5.6e+9; % radar operating frequency in Hz
g = 40.0; % antenna gain in dB
sigma = 0.1; % radar cross section in m squared
te =300.0; % effective noise temperature in Kelvins
nf = 5.0; %noise figure in dB
loss = 6.0; % radar losses in dB
range = [75e3,100e3,150e3]; % three range values
snr_db = linspace(5,20,200); % SNR values from 5 dB to 20 dB 200 points
snr = 10.^(0.1.*snr_db); % convert snr into base 10
gain = 10^(0.1*g); %convert antenna gain into base 10
loss = 10^(0.1*loss); % convert losses into base 10
F = 10^(0.1*nf); % convert noise figure into base 10
lambda = 3.e8 / freq; % compute wavelength
% Implement Eq.(1.57)
den = pt * gain * gain * sigma * lambda^2;
num1 = (4*pi)^3 * 1.38e-23 * te * F * loss * range(1)^4 .* snr;
num2 = (4*pi)^3 * 1.38e-23 * te * F * loss * range(2)^4 .* snr;
num3 = (4*pi)^3 * 1.38e-23 * te * F * loss * range(3)^4 .* snr;
tau1 = num1 ./ den ;
tau2 = num2 ./ den;
tau3 = num3 ./ den;
% plot tau versus snr
figure(1)
semilogy(snr_db,1e6*tau1,'k',snr_db,1e6*tau2,'k -.',snr_db,1e6*tau3,'k:')
grid
legend('R = 75 Km','R = 100 Km','R = 150 Km')
xlabel ('Minimum required SNR - dB');
ylabel ('\tau (pulse width) in \mu sec');

②、仿真

仿真参数参考上面代码

以下为不同检测距离，脉冲宽度相对所要求的 SNR 仿真

对三种不同的检测距离数值，脉冲宽度相对所要求的 SNR 曲线
结论：从图中可以看到随着雷达 SNR 的增加，脉冲宽度逐渐增大；对应于同一雷达 SNR，距离越远所需要的脉冲宽度越宽

3、功率孔径积相对于距离仿真 及 平均功率相对于孔径大小仿真

搜索雷达方程：$$SNR=\frac{P_{av}A\sigma }{4\pi k{T}_{e}FL{R}^4}\frac{T_{sc}}{\Omega }$$

功率孔径积：$P_{av}A$

①、Matlab 源码

power_aperture.m

function PAP = power_aperture(snr,tsc,sigma,range,te,nf,loss,az_angle,el_angle)
% This program implements Eq. (1.67)
Tsc = 10*log10(tsc); % convert Tsc into dB
Sigma = 10*log10(sigma); % convert sigma to dB
four_pi = 10*log10(4.0 * pi); % (4pi) in dB
k_db = 10*log10(1.38e-23); % Boltzman's constant in dB
Te = 10*log10(te); % noise temp. in dB
range_pwr4_db = 10*log10(range.^4); % target range^4 in dB
omega = (az_angle/57.296) * (el_angle / 57.296); % compute search volume in steraradians
Omega = 10*log10(omega); % search volume in dB
% implement Eq. (1.67)
PAP = snr + four_pi + k_db + Te + nf + loss + range_pwr4_db + Omega ...
    - Sigma - Tsc;
return

相关参数说明：

符号	描述	单位	状态
snr	灵敏度snr	dB	输入
tsc	扫描时间	s	输入
sigma	目标截面积	$m^2$	输入
range	目标距离（单位或矢量）	m	输入
te	有效噪声温度	K	输入
nf	噪声系数	dB	输入
loss	雷达损失	dB	输入
az_angle	搜索区域的方位角范围	${}^{\circ }$	输入
el_angle	搜索区域的俯仰角范围	${}^{\circ }$	输入
PAP	功率孔径积	dB	输出

fig1_16.m

close all
clear all
tsc = 2.5; % Scan time i s2.5 seconds
sigma = 0.1; % radar cross section in m sqaured
te = 900.0; % effective noise temperature in Kelvins
snr = 15; % desired SNR in dB
nf = 6.0; %noise figure in dB
loss = 7.0; % radar losses in dB
az_angle = 2; % search volume azimuth extent in degrees
el_angle = 2; %serach volume elevation extent in degrees
range = linspace(20e3,250e3,1000); % range to target from 20 Km 250 Km, 1000 points
pap1 = power_aperture(snr,tsc,sigma/10,range,te,nf,loss,az_angle,el_angle);
pap2 = power_aperture(snr,tsc,sigma,range,te,nf,loss,az_angle,el_angle);
pap3 = power_aperture(snr,tsc,sigma*10,range,te,nf,loss,az_angle,el_angle);
% plot power aperture prodcut versus range
% figure 1.16a
figure(1)
rangekm  = range ./ 1000;
plot(rangekm,pap1,'k',rangekm,pap2,'k -.',rangekm,pap3,'k:')
grid
legend('\sigma = -20 dBsm','\sigma = -10dBsm','\sigma = 0 dBsm')
xlabel ('Detection range in Km');
ylabel ('Power aperture product in dB');
% generate Figure 1.16b
lambda = 0.03; % wavelength in meters
G = 45; % antenna gain in dB
ae = linspace(1,25,1000);% aperture size 1 to 25 meter squared, 1000 points
Ae = 10*log10(ae);
range = 250e3; % rnage of interset is 250 Km
pap1 = power_aperture(snr,tsc,sigma/10,range,te,nf,loss,az_angle,el_angle);
pap2 = power_aperture(snr,tsc,sigma,range,te,nf,loss,az_angle,el_angle);
pap3 = power_aperture(snr,tsc,sigma*10,range,te,nf,loss,az_angle,el_angle);
Pav1 = pap1 - Ae;
Pav2 = pap2 - Ae;
Pav3 = pap3 - Ae;
figure(2)
plot(ae,Pav1,'k',ae,Pav2,'k -.',ae,Pav3,'k:')
grid
xlabel('Aperture size in square meters')
ylabel('Pav in dB')
legend('\sigma = -20 dBsm','\sigma = -10dBsm','\sigma = 0 dBsm')

②、仿真

仿真参数默认如下：

$\sigma$	$T_{sc}$	${\theta }_e={\theta }_a$	R	T_e	$nf\ast loss$	$snr$
$0.1m^2$	$2.5s$	$2^{\circ }$	$252km$	$900K$	$13dB$	$15dB$

1）、不同 RCS，功率孔径积相对于距离仿真

对三种不同的 RCS，功率孔径积相对于检测距离曲线
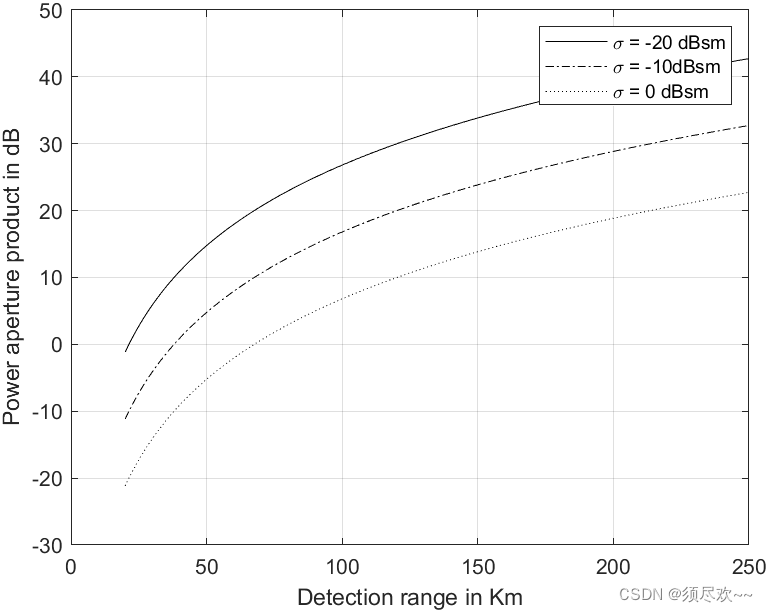
结论：从图中可以看到随着检测距离的增加，功率孔径积增大；雷达 RCS 越大，功率孔径积也越小

2）、不同 RCS，平均功率相对于孔径大小仿真

对三种不同的 RCS，雷达平均功率相对于孔径大小曲线
结论：从图中可以看到随着雷达孔径大小的增加，雷达平均功率呈现下降趋势；雷达 RCS 越大，雷达孔径越小

4、SNR 增益相对积累脉冲数仿真

• 相干积累：$$(SNR{)}_{CI}=n_p(SNR{)}_1$$
• 非相干积累：$$(SNR{)}_1=\frac{(SNR{)}_{NCI}}{2n_p}+\sqrt{\frac{(SN{R}_{NCI}^2)}{4N_P^2}+\frac{(SNR{)}_{(}NCI)}{n_p}}$$
  $$(SNR{)}_{NCI}=\frac{n_p(SNR{)}_1}{L_{NCI}}$$

注：$(SNR{)}_1$ 是产生给定检测概率所要求的单个脉冲的SNR

①、Matlab 源码

pulse_integration.m

function [snrout] = pulse_integration(pt, freq, g, sigma, te, b, nf, loss, range,np,ci_nci)
 snr1 = radar_eq(pt, freq, g, sigma, te, b, nf, loss, range) % single pulse SNR
 snr1=0
if (ci_nci == 1) % coherent integration
   snrout = snr1 + 10*log10(np);
else % non-coherent integration
    if (ci_nci == 2)
        snr_nci = 10.^(snr1./10);
        val1 = (snr_nci.^2) ./ (4.*np.*np);
        val2 = snr_nci ./ np;
        val3 = snr_nci ./ (2.*np);
        SNR_1 = val3 + sqrt(val1 + val2); % Equation 1.87 of text
        LNCI = (1+SNR_1) ./ SNR_1; % Equation 1.85 of text
        snrout = snr1 + 10*log10(np) - 10*log10(LNCI);
    end
end
return

相关参数说明：

符号	描述	单位	状态
pt	峰值功率	W	输入
freq	雷达中心频率	Hz	输入
g	天线增益	dB	输入
sigma	目标截面积	$m^2$	输入
te	有效噪声温度	K	输入
b	带宽	Hz	输入
nf	噪声系数	dB	输入
loss	雷达损失	dB	输入
range	目标距离（单位或矢量）	m	输入
np	积累脉冲数	无	输入
ci_nci	1是CI；2是NCI	无	输入
snr	SNR(单值或矢量，根据输入距离)	dB	输出

fig1_21.m

clear all
close all
np = linspace(1,10000,1000);
snrci = pulse_integration(4,94.e9,47,20,290,20e6,7,10,5.01e3,np,1);
snrnci = pulse_integration(4,94.e9,47,20,290,20e6,7,10,5.01e3,np,2);
semilogx(np,snrci,'k',np,snrnci,'k:')
legend('Coherent integration','Non-coherent integration')
grid
xlabel ('Number of integrated pulses');
ylabel ('SNR - dB');

②、仿真

仿真参数见上面源码

一般情况下 SNR 改善相对脉冲积累数

当使用积累时的 SNR 改善
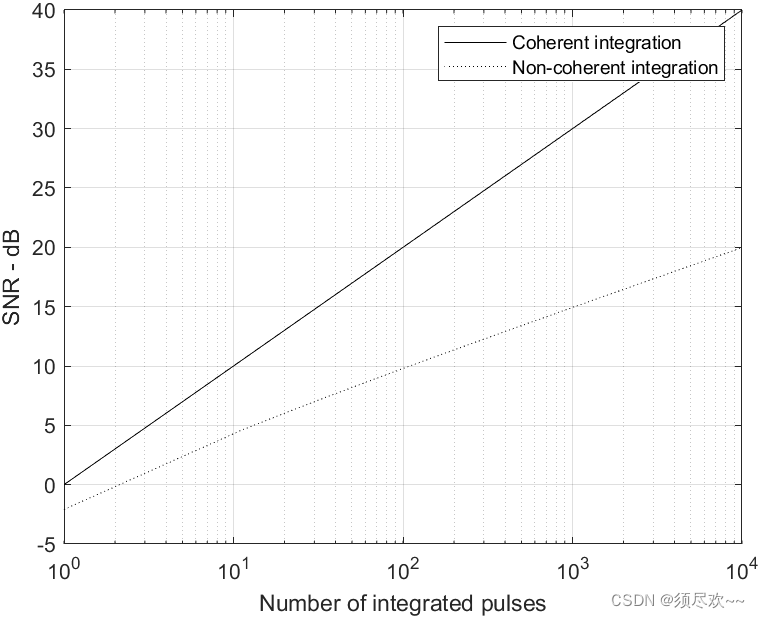
结论：从图中可以看到随着积累脉冲数的增加，雷达信噪比逐渐增大；且当积累脉冲数相等时，相干积累信噪比大于非相干积累信噪比

三、资源自取

雷达基础导论.pdf

---

我的qq：2442391036，欢迎交流！

---