目录
一、删除有序数组中的重复项,返回出现一次元素的个数。
二、原地移除数组中所有数值等于val的元素
三、合并两个有序数组
四、旋转数组
五、数组形式的整数加法
一、删除有序数组中的重复项,返回出现一次元素的个数。
26. 删除有序数组中的重复项 - 力扣(LeetCode)
给你一个 非严格递增排列 的数组
nums,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回nums中唯一元素的个数。数组大小numsSize已给出。考虑
nums的唯一元素的数量为k,你需要做以下事情确保你的题解可以被通过:
- 更改数组
nums,使nums的前k个元素包含唯一元素,并按照它们最初在nums中出现的顺序排列。nums的其余元素与nums的大小不重要。- 返回
k。
int removeDuplicates(int* nums, int numsSize) {
int src = 1;
int dst = 0;
while (src < numsSize) {
if (nums[src] == nums[dst])
src++;
else
nums[++dst] = nums[src++];
}
return dst + 1;
}思路:采用双指针一前一后
1、src负责寻找与当前dst相等的值,dst负责修改数组。

2、如果src等于dst,则src向后移动一位,向后寻找不相同的值

3、如果src不等于dst,则dst向后移动一位,将src的值赋值给dst,src向后移动一位继续循环比较后项元素。

4、src指向数组最后一个元素时,比较后src大于数组大小numsSize时停止循环。

5、返回值为新数组的大小dst+1。
二、原地移除数组中所有数值等于val的元素
27. 移除元素 - 力扣(LeetCode)
给你一个数组
nums和一个值val,你需要 原地 移除所有数值等于val的元素,并返回移后数组的新长度。不要使用额外的数组空间,你必须仅使用
O(1)额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
int removeElement(int* nums, int numsSize, int val) {
int src = 0;
int dst = 0;
while (src < numsSize) {
if (nums[src] != val)
nums[dst++] = nums[src++];
else
src++;
}
return dst;
}思路:采用双指针
src负责寻找值为val的位置,dst负责修改数组。假设当前val等于7。
1、如果src不等于val,则dst赋值为src,然后整体向后移动。

2、如果src等于val(dst也等于val),src向后移动一位。

3、再次判断时src不等于val,dst(当前为val)被赋值为src(val后一项)。成功删除数组元素val。

4、删除后dst和src均向后移动一位 。

5、之后在数组中依次查找,没有等于val的元素则将src赋值给dst(后项值一次赋值给前项),赋值后二者向后移动一位。
结果如下:

6、最终返回数组长度dst。
三、合并两个有序数组
88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组
nums1和nums2,另有两个整数m和n,分别表示nums1和nums2中的元素数目。请你 合并
nums2到nums1中,使合并后的数组同样按 非递减顺序 排列。注意:最终,合并后数组不应由函数返回,而是存储在数组
nums1中。为了应对这种情况,nums1的初始长度为m + n,其中前m个元素表示应合并的元素,后n个元素为0,应忽略。nums2的长度为n。示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6]
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
int end1 = m - 1;
int end2 = n - 1;
int i = m + n - 1;
while (end1 >= 0 && end2 >= 0) {
if (nums2[end2] > nums1[end1])
nums1[i--] = nums2[end2--];
else {
nums1[i--] = nums1[end1--];
}
}
while (end2 >= 0)
nums1[i--] = nums2[end2--];
}思路:三指针法
假设合并这两个数组:

1、定义 end1 和 end2 分别为数组 num1 和 num2 的最后一个元素下标,定义 i 为合并后num1新的最后一个元素下标.

2、因为是递增数列,所以我们从后向前先比较两个数组最后一个元素 (最大元素) 的大小。
大的元素赋值给数组num1尾节点,然后将 i、end1和end2向前移动一位继续比较。

3、如果end2位置元素不大于end1位置元素,则将end1位置元素赋值给 i 位置,end1和 i 向前移动一位。

4、最后end1已将小于零时,end2还等于0,证明数组num2中还有未合并的元素且该元素小于num1中最小元素(首元素)。

5、我们通过第二个循环将数组num2中小于num1最小元素的元素赋值到num1剩余位置,end2小于零时赋值结束。

当然也可以使用qsot排序做这道题,但时间复杂度为O(nlogn)大于上述解法的O(m+n)。
所以综合考虑推荐三指针法!!!
四、旋转数组
189. 轮转数组 - 力扣(LeetCode)
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]
void reserve(int* a, int left, int right)
{
while (left < right) {
int tmp = a[left];
a[left] = a[right];
a[right] = tmp;
left++;
right--;
}
}
void rotate(int* nums, int numsSize, int k) {
if (k > numsSize)
k %= numsSize;
reserve(nums, numsSize - k, numsSize - 1);
reserve(nums, 0, numsSize - k - 1);
reserve(nums, 0, numsSize - 1);
}
思路:使用三次逆转法,让数组旋转k次
- 逆转子数组[numsSize - k, numsSize - 1]
- 逆转子数组[0, numsSize - k - 1]
- 整体逆转[0,numsSize - 1]
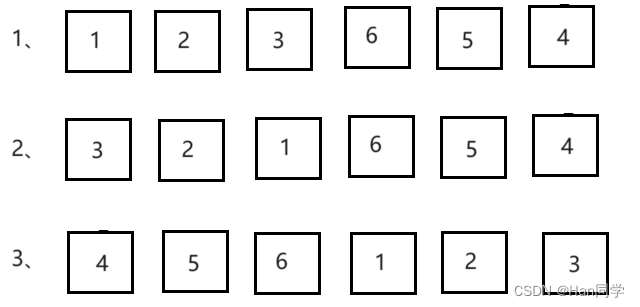
假设轮转次数k为3
1、首先写出逆转数组的函数reserve,逆置的原理就是依次交换首尾元素。

2、然后找到要逆转的数组对应部分进行逆转。

3、 逆转过程如下:
五、数组形式的整数加法
989. 数组形式的整数加法 - 力扣(LeetCode)
整数的 数组形式
num是按照从左到右的顺序表示其数字的数组。
- 例如,对于
num = 1321,数组形式是[1,3,2,1]。给定
num,整数的 数组形式 ,和整数k,返回 整数num + k的 数组形式 。示例 1:
输入:num = [1,2,0,0], k = 34 输出:[1,2,3,4] 解释:1200 + 34 = 1234
int* addToArrayForm(int* A, int ASize, int K, int* returnSize) {
int* addRet = (int*)malloc(10001 * sizeof(int));
//reti: 第i位的结果
int reti = 0;
//从低位开始相加
int ai = ASize - 1;
int next = 0; // 进位值
while (ai >= 0 || K > 0)
{
int x1 = 0;
//如果ai没有越界,还有未相加的位,取出一位存入x1
if (ai >= 0)
{
x1 = A[ai];
--ai;
}
int x2 = 0;
//如果k大于0,获取k的第i位
if (K > 0)
{
x2 = K % 10;
K /= 10;
}
//第i位的结果:每一位的值 + 进位
int ret = x1 + x2 + next;
//如果结果大于9,需要进位
if (ret > 9)
{
ret %= 10;
next = 1;
}
else
{
next = 0;
}
//存入第i位的结果到数组中
addRet[reti++] = ret;
}
//如果最高位有进位,需要在存入1
if (next == 1)
{
addRet[reti++] = 1;
}
//逆置结果
reverse(addRet, 0, reti - 1);
*returnSize = reti;
return addRet;
}思路:模拟加法进行逐位相加, 从低位向高位相加,最后整体逆置,得到最终结果
1、定义一个整数数组
addRet用于存储相加的结果。数组的大小设为10001,足够容纳可能的最大结果。定义变量
reti,表示结果数组的当前索引,初始化为0。定义变量
ai,表示数组A的当前索引,初始化为ASize - 1,即数组A的最高索引。定义变量
next,表示进位值,初始化为0。int* addRet = (int*)malloc(10001 * sizeof(int)); int reti = 0; int ai = ASize - 1; int next = 0;
2、使用循环处理每一位的相加,循环条件是
ai >= 0或K > 0,即数组A还有位数未相加,或者K还有位数未相加。while (ai >= 0 || K > 0)
3、在循环内部,首先获取
A数组当前位的值x1,如果ai没有越界,就取出对应位置的值,并将ai减1。int x1 = 0; if (ai >= 0) { x1 = A[ai]; --ai; }
4、获取整数
K的当前位值x2,如果K大于0,就取出K的最低位,同时将K除以10,以准备处理下一位。int x2 = 0; if (K > 0) { x2 = K % 10; K /= 10; }
5、计算当前位的结果
ret,是x1、x2和之前的进位next三者之和。如果结果大于9,表示需要进位,就对结果取模10,然后将next设置为1;否则,next设置为0。int ret = x1 + x2 + next; if (ret > 9) { ret %= 10; next = 1; } else { next = 0; }
7、将计算得到的
ret存入结果数组addRet的当前位置reti,递增reti,以准备处理下一位。addRet[reti++] = ret;
8、循环结束后,检查最高位是否有进位。如果
next为1,表示有进位,因此将1存入结果数组的当前位置reti。if (next == 1) { addRet[reti++] = 1; }
9、调用
reverse函数来逆置结果数组addRet,以得到正确的结果顺序。reverse(addRet, 0, reti - 1);
最后,将结果数组的大小
reti赋值给returnSize指向的变量,以告知结果数组的大小。返回结果数组
addRet,它包含了相加的结果。*returnSize = reti; return addRet;