文章目录
- 如何判断凸函数
- 常见的凸函数
- 复合函数判断是否凸函数
- 对于约束问题
- 使用泰勒公式进行松弛
- 参考文献
如何判断凸函数
当满足下面的公式时候可以判断目标函数为凸函数
f
(
ξ
x
+
(
1
−
ξ
)
y
)
<
ξ
f
(
x
)
+
(
1
−
ξ
)
f
(
y
)
f(\xi x+(1-\xi)y)<\xi f(x)+(1-\xi)f(y)
f(ξx+(1−ξ)y)<ξf(x)+(1−ξ)f(y)
通常也可以根据一阶条件和二阶条件进行判断。
常见的凸函数
− l o g ( ) x -log()x −log()x, x l o g ( x ) xlog(x) xlog(x), e a x e^{ax} eax,max,Log-sum-exp
复合函数判断是否凸函数
对于复合函数
h
(
g
(
x
)
)
h(g(x))
h(g(x))
如果h是凸函数,则需要分析h的单调性。如果h单增,则g是凸函数才能保证复合函数是凸函数;如果h单减,则g是凹函数才能保证复合函数是凸函数。
如果h是凹函数。如果h单增,则g是凹函数才能保证复合函数是凸函数;如果h单减,则g是凸函数才能保证复合函数是凸函数。
对于约束问题
如果目标函数和约束条件都是凸函数,则可以称此时的优化问题为凸规划,这也是在计算的时候期待变换成的。
当目标函数和约束条件出现非凸的情况可以使用松弛方法进行变形,用对应的上界或者下界进行替换。然后进而可以使用相应的凸规划方法进行求解。
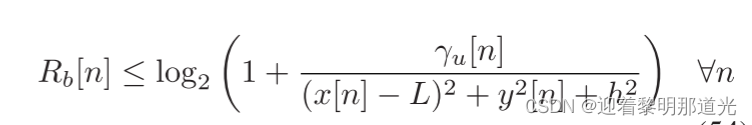
对于约束条件,log()函数是凹函数,并且是单调递增的。通过计算Hessian矩阵,可以发现里面是凸函数,因此这个复合函数是一个凹函数。
使用泰勒公式进行松弛
泰勒公式可以写为
f
(
x
)
<
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
f(x)<f(x_0)+f'(x_0)(x-x_0)
f(x)<f(x0)+f′(x0)(x−x0)
定义
η
2
[
n
]
=
(
x
[
n
]
−
L
)
2
+
y
2
[
n
]
+
h
2
η_2[n] =(x[n] − L)^2 + y^2[n]+ h^2
η2[n]=(x[n]−L)2+y2[n]+h2
可以对
η
2
[
n
]
η_2[n]
η2[n]进行变换,因此得到
l
o
g
2
(
1
+
γ
u
[
n
]
/
η
2
[
n
]
)
>
R
b
L
B
log_2(1+ \gamma_u[n]/ η_2[n] )>{R_b}^{LB}
log2(1+γu[n]/η2[n])>RbLB
从而原始的约束就可以转换成凸的。
参考文献
Secure UAV Relay Communication via PowerAllocation and Trajectory Planning