🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨
🐻强烈推荐优质专栏: 🍔🍟🌯C++的世界(持续更新中)
🐻推荐专栏1: 🍔🍟🌯C语言初阶
🐻推荐专栏2: 🍔🍟🌯C语言进阶
🔑个人信条: 🌵知行合一
🍉本篇简介:>:非递归实现二叉树的前中后序遍历.
金句分享:
✨不要慌,不要慌,太阳下了,有月光!✨
前言
为什么要掌握非递归呢?
递归实现前中后序遍历十分轻松,二非递归就复杂许多了.
主要是递归有以下几个缺陷：
-
内存消耗：递归算法由于会在堆栈中不停地压入和弹出函数调用记录，因此会占用大量的内存，如果递归的次数过多，可能会导致栈溢出。
-
效率低下：递归算法的效率低下，因为每次递归都需要重新压入调用记录和恢复上一次的状态，这些操作都会增加额外的开销，导致递归算法效率低下，特别是在处理大量数据时会更为明显。
-
可读性较差：递归算法的代码一般会比较复杂，理解和维护难度较大，而且递归算法往往涉及到栈的使用，在理解和分析时需要一定的数学基础。
总结:主要害怕栈溢出,其次,可以增加一点点效率.
一、非递归实现"前序遍历"
题目链接:传送门
题目要求:
给你二叉树的根节点 root ，返回它节点值的 前序 遍历。
补充知识:
二叉树的前序遍历，又称为先序遍历，是指先访问节点本身，然后按照先左后右的顺序遍历其左右子树。具体步骤如下：
- 访问根节点。
- 遍历左子树，即对左子节点进行前序遍历。
- 遍历右子树，即对右子节点进行前序遍历。
方法一、思路分析:
- 根节点入栈.
- 栈顶元素入存入
vector,根节点出栈. - 右孩子入栈
- 左孩子入栈
因为我们要求:
先访问左孩子,再访问右孩子.
而栈是后进先出的结构,所以:
右孩子先入栈,左孩子后入栈.
步骤示例图:
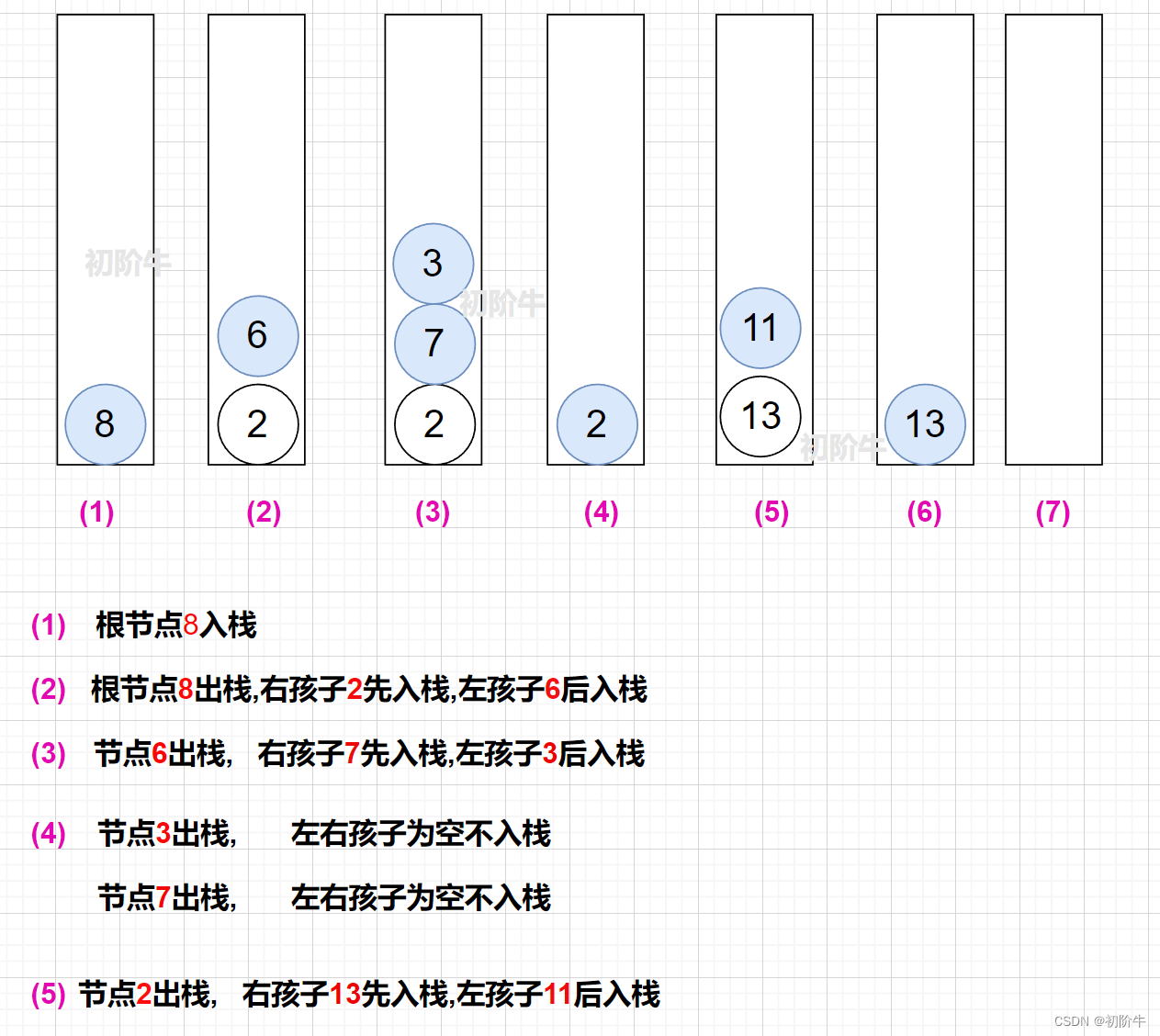(图片为博主:"初阶牛"原创,未经允许,不得复制)
结果:
🍔非递归代码实现1:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> s1;
vector<int> v1;
s1.push(root);//根节点先入栈
while (!s1.empty()) { //当栈为空时,结束
TreeNode* top = s1.top();
if(top==nullptr)break;
v1.push_back(top->val); //出栈前,先将栈顶元素存入vector
//栈顶元素出栈
s1.pop();
//栈顶元素的右左子树入栈
if (top->right)
s1.push(top->right);
if (top->left)
s1.push(top->left);
}
return v1;
}
};
方法二、思路分析
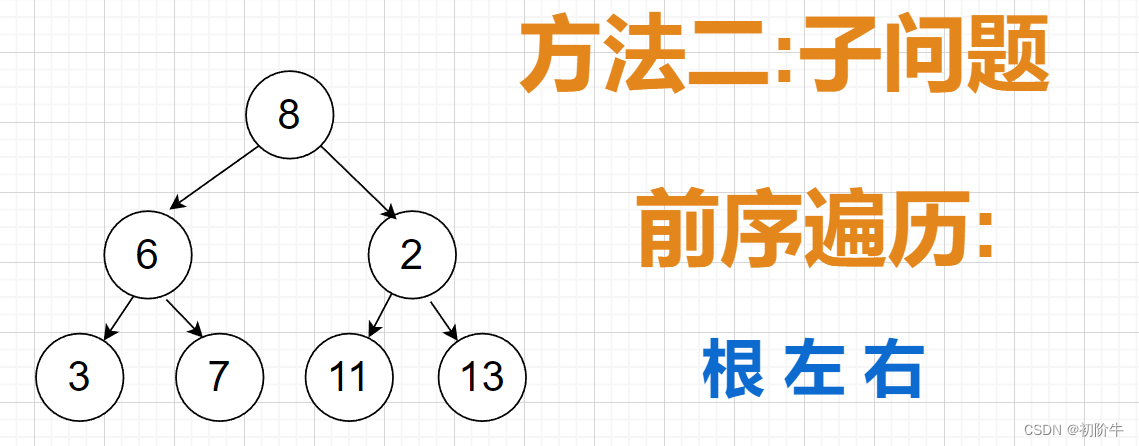
- 左路节点一边存入vector,一边入栈.
- 栈顶元素出栈,如果栈顶元素有右子树,则将右子树转化为子问题,和步骤1一样.
注意循环的结束条件.
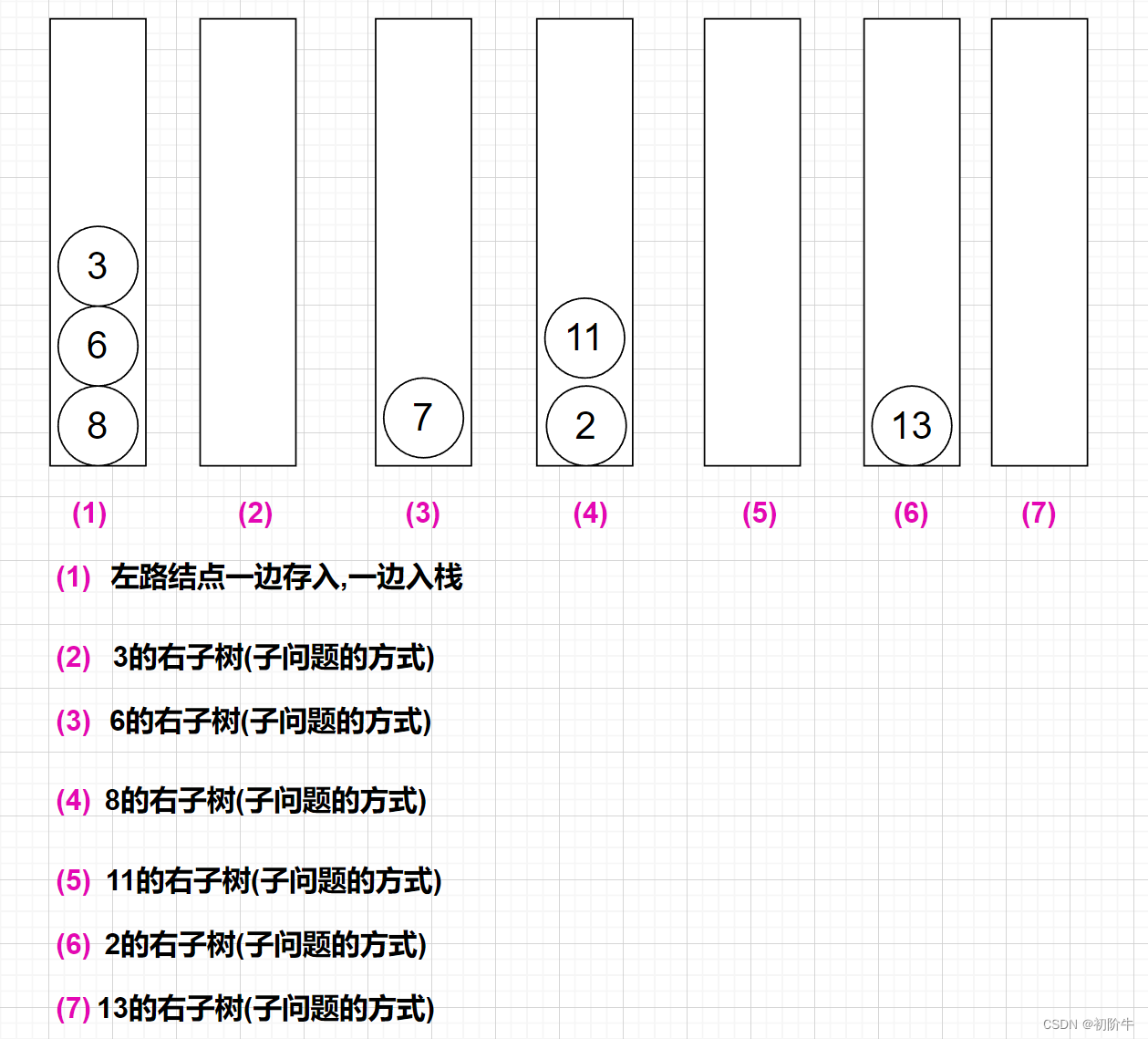(图片为博主:"初阶牛"原创,未经允许,不得复制)
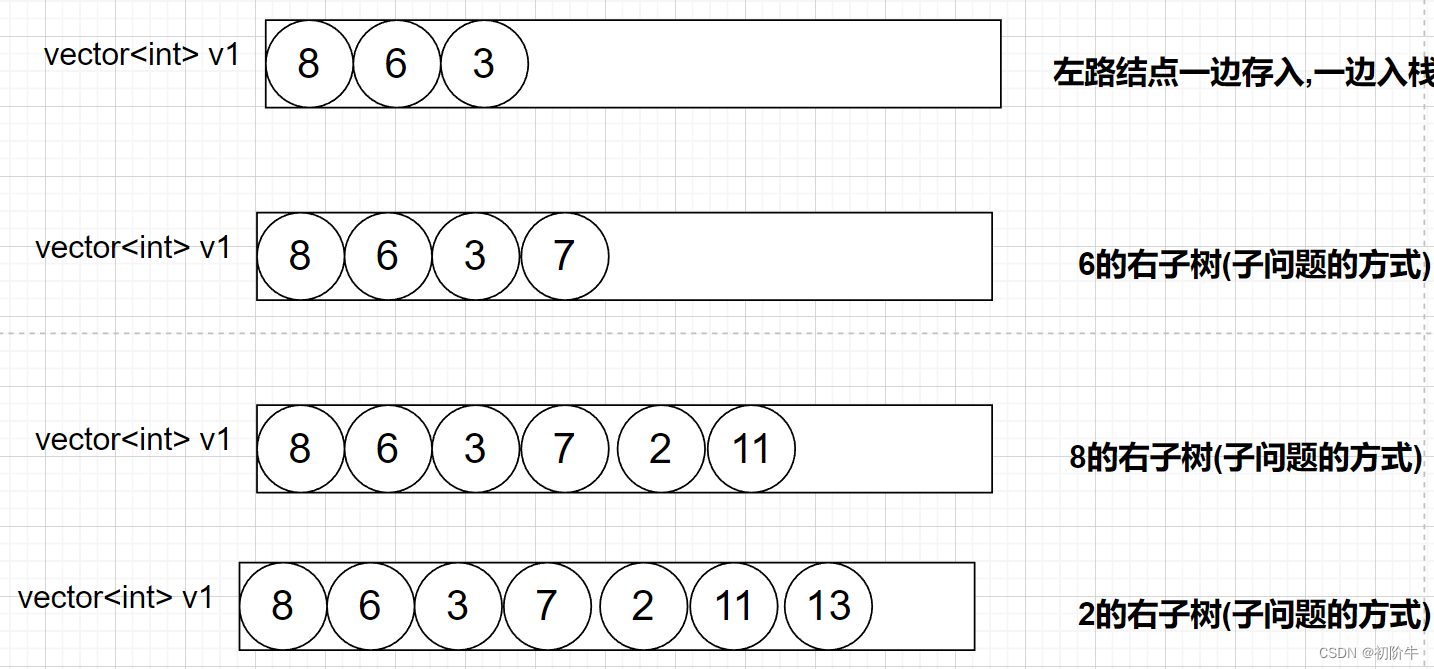
(图片为博主:"初阶牛"原创,未经允许,不得复制)
🍉非递归实现2:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> v1;
stack<TreeNode*> s1;
TreeNode* cur=root;
while(cur || !s1.empty()){
//将左路节点全部存入栈
while(cur){
v1.push_back(cur->val);
s1.push(cur);
cur=cur->left;
}
//栈顶元素出栈
TreeNode*top=s1.top();
s1.pop();
//如果栈顶元素的右子树存在,则转化为子问题解决.
if(top->right)
cur=top->right; //关键语句,通过让cur等于栈顶元素的右子树.
}
return v1;
}
};
二、非递归实现"中序遍历"
题目链接:传送门
题目描述:
给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。
补充知识:
二叉树的中序遍历指的是按照从小到大的顺序，依次访问二叉树中的所有节点。即先访问左子树，再访问根节点，最后访问右子树。
中序遍历算法如下：
- 如果当前节点的左子树非空，则递归遍历左子树。
- 访问当前节点。
- 如果当前节点的右子树非空，则递归遍历右子树。
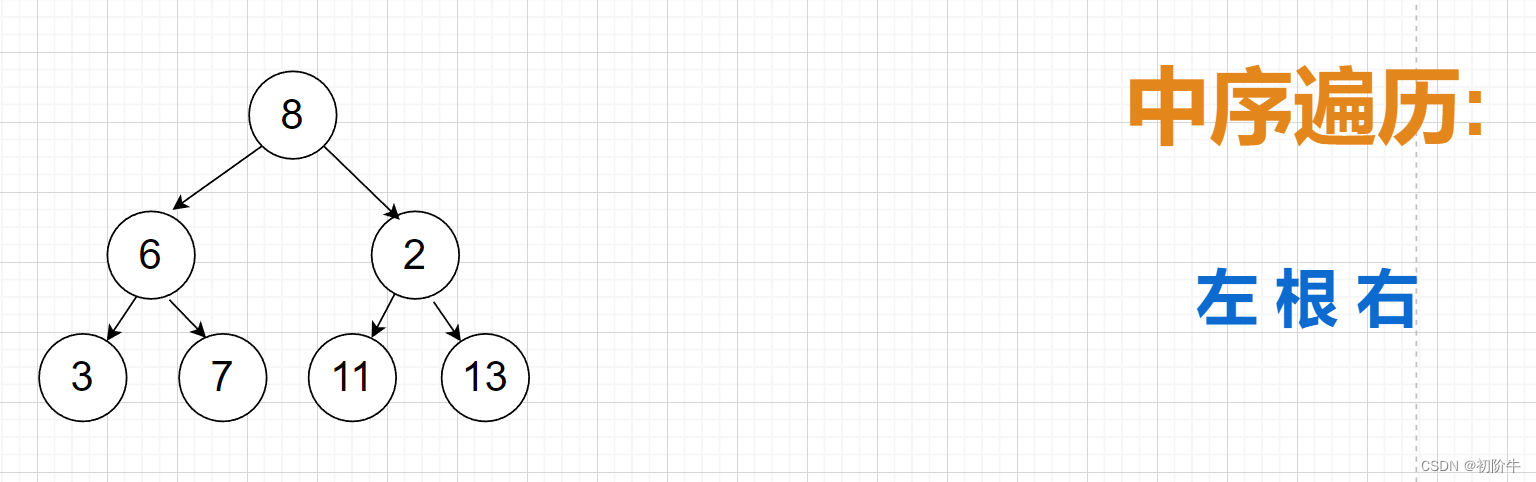
思路分析:
有了前面的前序遍历的思想,对于中序遍历,需要注意的是存入容器(这里是vector)的时机.
- 左路节点依次入栈.(与前序对比:此时入栈并没有入容器.)
- 栈顶元素入容器,栈顶元素出栈,栈顶元素的右子树子问题解决.
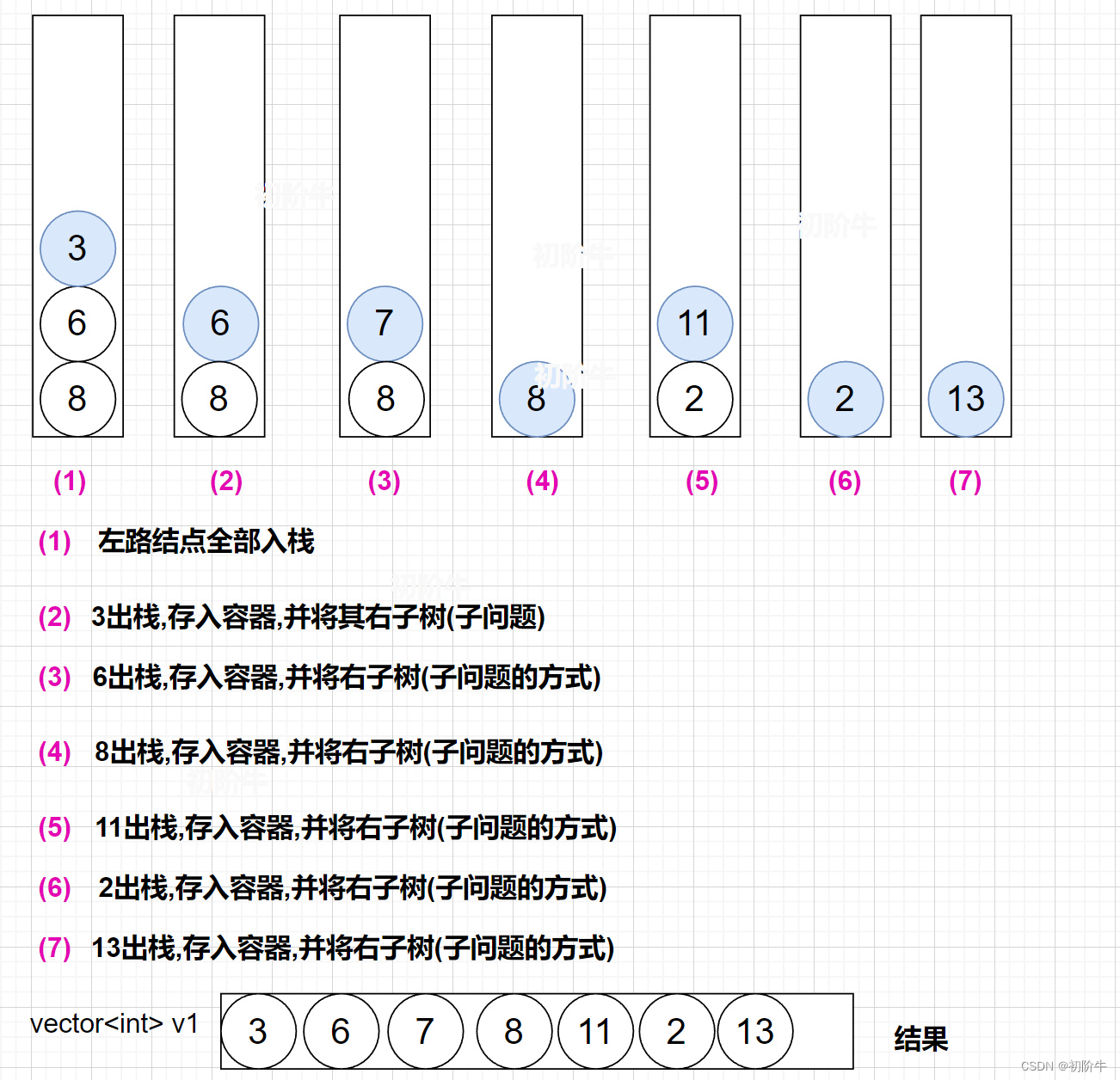
(图片为博主:"初阶牛"原创,未经允许,不得复制)
🔑非递归代码实现:
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
stack<TreeNode*> s1;
vector<int> v1;
TreeNode* cur=root;
while(cur||!s1.empty()){
//沿着左子树一直入节点
while(cur){
s1.push(cur);
cur=cur->left;
}
TreeNode* top = s1.top();
if(top==nullptr)break;
v1.push_back(top->val);
//栈顶元素出栈
s1.pop();
//右子树 以子问题的方式解决
if(top->right)
cur=top->right;
}
return v1;
}
};
三、非递归实现"后序遍历"
题目链接:传送门
题目描述:
给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。
二叉树的后序遍历指的是先访问左右子树，最后访问根节点的顺序遍历。即先遍历左子树，再遍历右子树，最后访问根节点。
后序遍历算法如下：
- 如果当前节点的左子树非空，则递归遍历左子树。
- 如果当前节点的右子树非空，则递归遍历右子树。
- 访问当前节点。
思路分析
对于后序遍历,同样注意存入容器的时机,应当是左子树和右子树都访问完毕,才能够访问根节点.
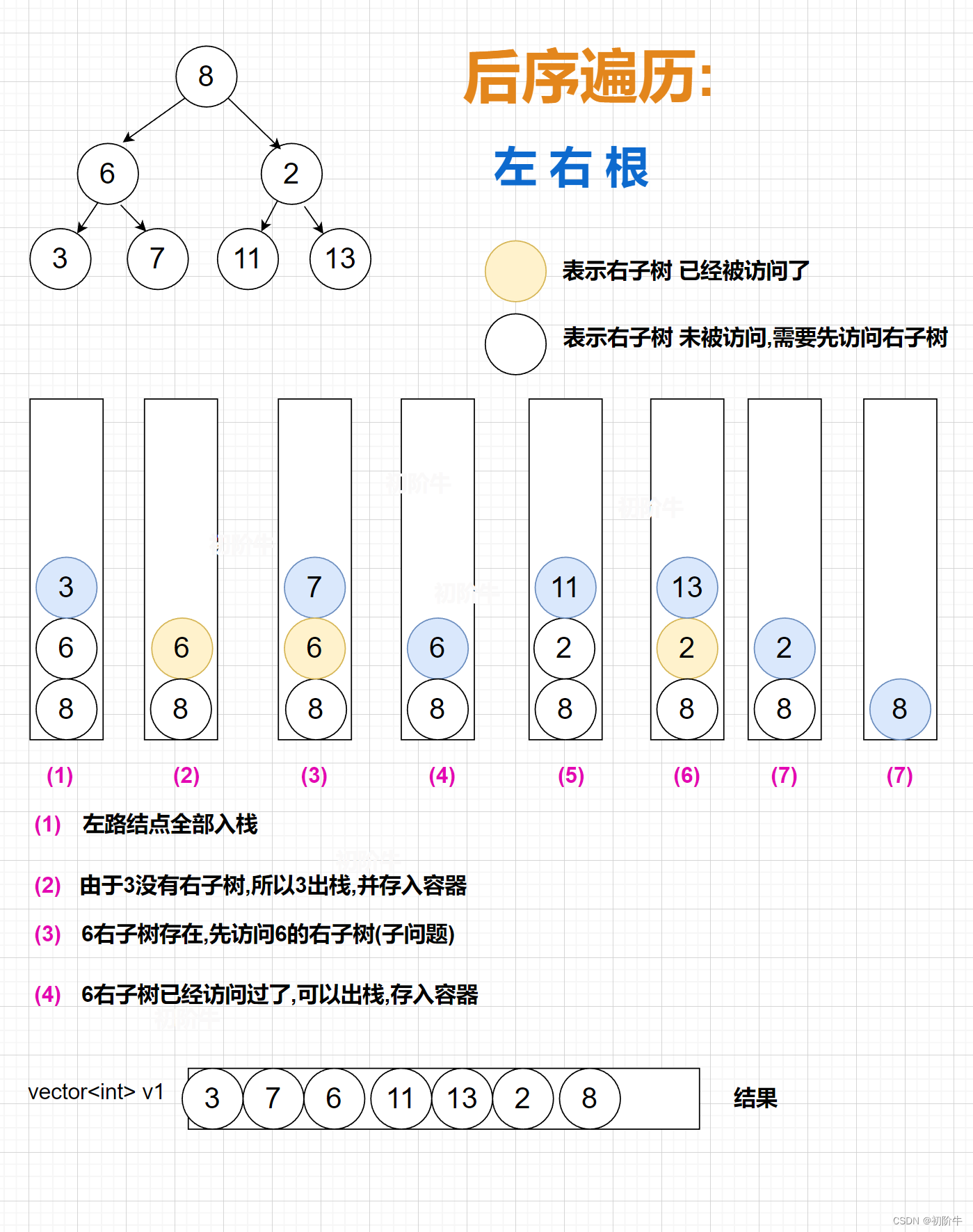
注意点:
(1)访问结点之前,需要先判断右子树是否已经被访问.
如何判断根节点的右子树已经有没有访问?
答案: 上一个存入的结点是自己右子树,则右子树已经被访问.
上一个结点不是自己的右子树,则右子树未被访问.
示例:
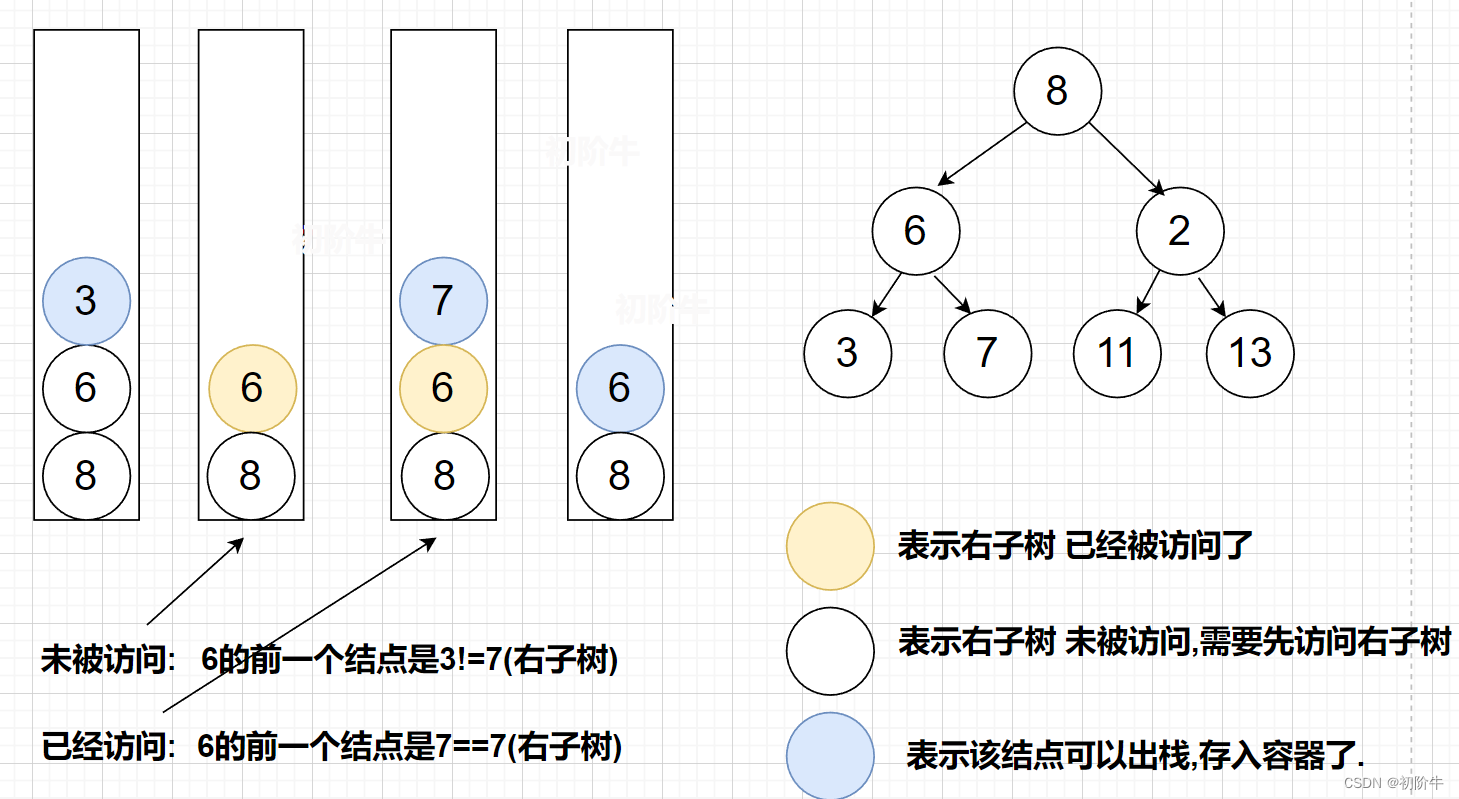
💗非递归代码实现:
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> s1;
vector<int> v1;
TreeNode* prv = nullptr;
TreeNode* cur = root;
while (cur || !s1.empty()) {
//沿着左子树一直入节点
while (cur) {
s1.push(cur);
cur = cur->left;
}
TreeNode* top = s1.top();
if (top == nullptr)break;
//右子树 以子问题的方式解决
if (prv!=top->right && top->right) {
cur = top->right;
continue;
}
prv=top;
v1.push_back(top->val);
//栈顶元素出栈
s1.pop();
}
return v1;
}
};
