题目

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = “babad” 输出：“bab” 解释：“aba” 同样是符合题意的答案。 示例 2：

输入：s = “cbbd” 输出：“bb” 示例 3：

输入：s = “a” 输出：“a” 示例 4：

输入：s = “ac” 输出：“a”

思路

回文子串，立即推->

①动态规划（两端收缩法，相同则i++，j–继续比较）
②双指针法（两种中心扩散法）

其中动态规划空间复杂度比较高

方法一：动态规划

动规五部曲：

1. 确定dp数组和下标含义
   布尔类型的dp[i][j]:表示区间[i，j]的子串是否是回文子串，如果是的话则dp[i][j] 为 true

2. 确定递推公式
   分为来两种情况：
   （1）s[i] ！= s[j]，不相等的话dp[i][j]一定为false
   （2）s[i] == s[j]，这里有三个情况
   情况一：下标i 与 j相同，即i == j，同一个字符例如a，当然是回文子串
   情况二：下标i 与 j相差为1或者为2时，即j- i == 1，或者j- i == 2，例如aa，axa也是回文子串
   情况三：下标 i 与 j相差大于1的时候，即，j - i > 1，例如cabac，此时s[i]与s[j]已经相同了，看[i，j]区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 [i+1 ， j-1]区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true

3. 初始化dp
   dp[i][j]初始化为false

4. 确定遍历顺序
   
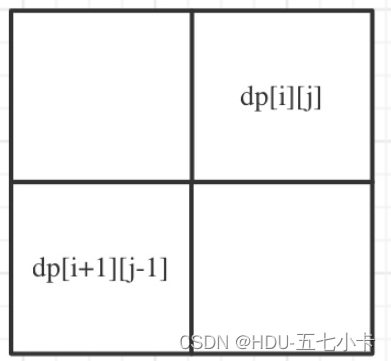
   所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的，有的代码实现是优先遍历列，然后遍历行，其实也是一个道理，都是为了保证dp[i + 1][j - 1]都是经过计算的。

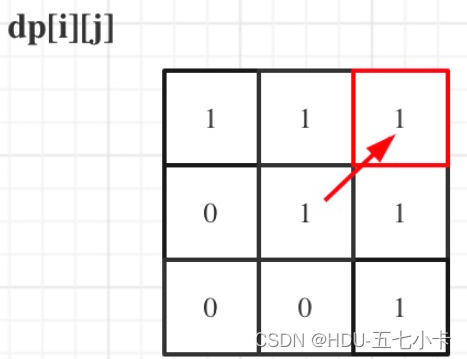
5. 举例推导dp数组
   举例，输入：“aaa”，dp[i][j]状态如下：
   
   java代码如下：

class Solution {
	public String longestPalindrome(String s){
		if(s.length() == 0 || s.length() == 1) return s;
		int n = s.length();
		int maxLen = 1;//记录最长子串长度
		int begin = 0;//每一个开始判断的回文子串的起始位置
		// dp[i][j] 表示 [i,j]范围的子串是否是回文串
		boolean[][] dp = new boolean[n][n];
		//初始化：所有长度为 1 的子串,即区间[i,i]的子串都是回文串
		for(int i = 0; i < n; i++){
			dp[i][i] = true;
		}
		
		char[] chars = s.toCharArray();
		//先枚举子串的长度，长度为1的子串已经考虑过了，从长度2开始,一直到整个字符串
		for(int L = 2; L <= n; L++){
			//枚举左边界
			for(int i = 0; i < n; i++){
				//由L和i可以确定右边界，即 L = j - i + 1 => j = L + i - 1
				int j = L + i - 1;
				//如果右边界越界，则终止循环
				if(j >= n) break;
				
				if(chars[i] != chars[j]){
					dp[i][j] = false;
				} else {
					if(j - i <= 2){
						dp[i][j] = false;
					} else {
						dp[i][j] = dp[i+1][j-1];
					}
				}
				 // 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
				 if(dp[i][j] && j - i + 1 > maxLen){
				 	maxLen = j - i + 1;
				 	begin = i; 
				 }
			}
		}
		return s.subString(begin,begin + maxLen);
	}
}

方法二：双指针法/中心扩散法

确定回文串，就是找中心然后向两边扩散看是不是对称的就可以了，确定有多少个回文字串，中心扩散法，可以理解为，遍历每个中心点，判断每个中心点左右是不是回文串，是的话左–右++再继续判断

只不过在遍历中心的时候，中心点会有两种情况：
一个元素可以作为中心点，两个元素也可以作为中心点，给定一个字符串s，长度为len，则中心点的个数为2 * len - 1，分别是len个单字符和len-1个双字符，如 “abcde”，那么可能的中心点为“a”、“b”、“c”、“d”、“e”、“ab”、“bc”、“cd”、“de”一共2 * 5-1=9个

所以要分两种情况讨论：一个中心点和两个中心点

java代码如下：

class Solution {
	public String longestPalindrome(String s){
		String s1 = "";//一个中心点开始扩散的结果
		String s2 = "";//两个中心点开始扩散的结果
		String res = "";//记录以一个为中心点和以两个为中心点扩散结果的最长子串
		for(int i = 0; i < s.length(); i++){
			// 分两种情况：即一个元素作为中心点，两个元素作为中心点
			s1 = extend(s,i,i);//情况一
			res = s1.length() > res.length() ? s1 : res;//记录最长的回文子串
			s2 = extend(s,i,i+1);//情况二
			res = s2.length() > res.length() ? s2 : res;
		}
		return res;//返回最长的
	}
	public String extend(String s, int start, int end){
		String tmp = "";
		while(start > 0 && end < s.length() && s.chatAt(start) == s.charAt(end)){
			tmp = s.subString(start,end + 1); //Java中substring是左闭右开的，所以要+1
			//向两边扩散
			start++;
			end--;
		}
		return tmp;
	}
}