前言

❤️ 铁汁们大家好，欢迎大家来到出小月的博客里， 🤗🤗🤗之前呢，我分享了数据结构的栈和队列。。。。今天呢，给大家分享关于树的内容包括了树的结构、遍历和一些题目，希望大家看完我这篇文章都能够“涨芝士”，感觉小月写的还不错的话，记得👍🏻点赞加关注😘鼓励一下博主哦，不然下次可找不到我啦❗❗

---

作者简介

❤️ 作者的gitee:出小月；
❤️ 作者的主页：出小月的《程序员历险记》
❤️专栏：《C语言》,《数据结构初阶》
😊希望大家都能够：好好学习，天天编程❗❗❗

---

---

一、树概念及结构

🤗之前呢，我分享了顺序表、链表、栈和队列。这些都是线性结构，今天呢分享树的知识点，树呢是一种非线性的数据结构。把它叫做树呢？是因为它看起来像一颗倒挂的树，也就是说根朝上，而叶子朝下。

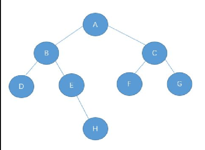
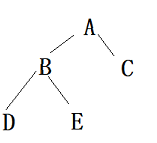
🤗这就是一棵树，那它怎么表示的呢？我们一般用左孩子、右兄弟。

typedef char tdatatype;
struct node
{
	struct node* firstchild;//第一个孩子节点
	struct node* nextbrother;//指向其下一个兄弟结点
	tdatatype data;
};

二、二叉树结构及遍历

1、二叉树性质

1、若根节点层数为i，则一颗非空二叉树的第i层上最多有2^(i-1)；
2、若根节点层数为i，则深度为H的最大二叉树的最大节点数为（2^H）-1；
3、对于任何一颗二叉树，如果度为0其叶节点个数为n0，度为2的分支节点个数为n2，则有
n0=n2+1；

1、二叉树结构

🐹我们重点说的是二叉树。。。
任何一个二叉树都可以分成三个部分：
0️⃣ 根节点
1️⃣ 左子树
2️⃣ 右子树
我们这主要用的是分治算法：分而治之，大问题分成类似子问题，子问题再分成子问题……
那这是不是可以用递归啦？直到子问题不可再分割❗❗❗

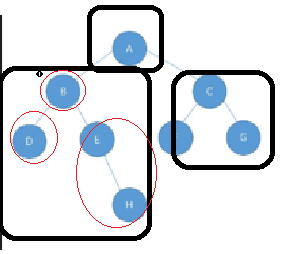
🐷就像这个二叉树本来可以分为以A结点为根节点，还有左子树，右子树；
然后左子树又可以分成以B为根节点，还有左子树，右子树；
右子树也可以分成以C为根节点，还有左子树，右子树；

2、特殊的二叉树

1️⃣ 满二叉树

一个二叉树，如果每一层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是，如果一个二叉树N层，且总结点的个数是(2^N)-1,则它就是满二叉树。

2️⃣完全二叉树

完全二叉树由满二叉树而引出来，对于深度为k的，有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号从1-n的结点一一对应时称之为完全二叉树。

满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树

3、二叉树的遍历

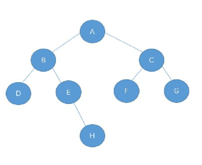
1️⃣前序遍历

🐱就是先访问根节点，再访问左子树，最后访问右子树
就上面的树，我们先访问A结点
再访问左子树：左子树先访问B结点，再访问B结点的左子树D结点，然后再访问B结点的右子树，右子树先访问E结点，没有左子树，再访问H结点；
接下来访问右子树：先访问C结点，在访问左子树F结点，再访问右子树G结点

递归图就是这⬇️，大家一定要自己动手画一画，更加容易理解。。。

递归展开图比较复杂就展开一个简单的吧上面的⬆️

代码如下：

void prevorder(bitree* root)//递归前序 
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	prevorder(root->left);
	prevorder(root->right);
}

2️⃣中序遍历

🐱就是先访问左子树，再访问根节点，最后访问右子树
代码如下：

void inorder(bitree* root)//递归中序
{
	if (root == NULL)
	{
	   printf("NULL ");
	   return;
	}
	inorder(root->left);
	printf("%c", root->data);
	inorder(root->right);
}

3️⃣后序遍历

🐱就是先访问根结点，再访问左子树，最后访问右子树

代码如下：

void lastorder(bitree* root)//递归后序
{
    if (root == NULL)
	{
	   printf("NULL ");
	   return;
	}
	lastorder(root->left);
	lastorder(root->right);
	printf("%c", root->data);
}

4️⃣层序遍历

🤗层序遍历的核心：首先将二叉树的根节点入队中，判断队列不为空，就输出队头的元素，
如果这个结点有孩子，就将孩子入队，将遍历过的节点出队列，循环以上操作，直到树为空

typedef struct queuenode
{
	struct queuenode* next;
	char data;
}qnode;
typedef struct queue
{
	qnode* head;
	qnode* tail;
}queue;
void levelorder(bitree* root)//非递归的层序遍历（用队列实现）核心：上一层带下一层
{
	queue q;
	queueinit(&q);
	if (root)
	{
		queuepush(&q, root);//头结点进栈
		while (!queueempty(&q))//如果这个队列不为空
		{
			bitree* front = queuefront(&q);//就出栈
			queuepop(&q);
			printf("%c", front->data);//并打印
			if (front->left)//如果这个结点的左子树存在就进队列
			{
				queuepush(&q, front->left);
			}
			if (front->right)//如果这个结点的右子树存在就进队列
			{
				queuepush(&q, front->right);
			}
		}
	}
}

三、二叉树常见OJ题练习

1、树的结点的个数

🐻这里用了一个三目运算符，如果这个结点是空就是0个结点，如果不为空就递归的遍历左子树的结点，和右子树的结点，还要加上根节点这个结点

int treesize(bitree* root)
{
	return root == NULL ? 0 : treesize(root->left) + treesize(root->right) + 1;
}

2、叶子节点的个数

🐻叶子节点就是左子树和右子树都为0的结点，因此只一左子树和右子树都为0的这个结点返回1，然后递归遍历左子树，右子树。

int treeleafsize(bitree* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return treeleafsize(root->left) + treeleafsize(root->right);
}

3、主函数

🐻这里我建了一棵树

int main()
{
	bitree* A = (bitree*)malloc(sizeof(bitree));
	A->data = 'A';
	A->left = NULL;
	A->right = NULL; 
	bitree* B = (bitree*)malloc(sizeof(bitree));
	B->data = 'B';
	B->left = NULL;
	B->right = NULL;
	bitree* C = (bitree*)malloc(sizeof(bitree));
	C->data = 'C';
	C->left = NULL;
	C->right = NULL;
	bitree* D = (bitree*)malloc(sizeof(bitree));
	D->data = 'D';
	D->left = NULL;
	D->right = NULL;
	bitree* E = (bitree*)malloc(sizeof(bitree));
	E->data = 'E';
	E->left = NULL;
	E->right = NULL;
	A->left = B;
	A->right = C;
	B->left = D;
	B->right = E;
	prevorder(A);//前序遍历
	return 0;
}

总结

🤗🤗今天关于树的知识点就分享到这里了，感觉小月写的还不错的话，记得点赞加关注哦👍👍，小月一直会分享记录自己的学习过程哦❗❗❗