变分自编码器(VAE)是一种应用广泛的无监督学习方法，它的应用包括图像生成、表示学习和降维等。虽然在网络架构上经常与Auto-Encoder联系在一起，但VAE的理论基础和数学公式是截然不同的。本文将讨论是什么让VAE如此不同，并解释VAE如何连接“变分”方法和“自编码器”。

本文更专注于VAE的统计概念和推导。我们将从介绍VAE所要解决的问题开始，解释变分方法在解决方案中所起的作用，并讨论VAE与AE之间的联系。最后还会将VAE应用于图像重建任务来进行具体的演示。

我们考虑一个由随机变量x的N个i.i.d.样本(标量或向量)组成的数据集。假设数据是由一些随机过程产生的，这里包含一个未观察到的随机变量z(即潜在变量)。

生成过程有两个步骤:

值 z⁽ⁱ⁾ 是从某个先验分布 p(z; θ) 生成的， 值 𝐱⁽ⁱ⁾ 是从一些依赖于 𝐳⁽ⁱ⁾ 的条件分布 p(x|z=𝐳⁽ⁱ⁾; θ) 生成的，

其中先验p(z;θ)和条件似然p(x|z;θ)都是未知参数集θ的参数分布。

我们感兴趣的是与给定场景相关的以下三个问题:

• 参数集θ的MAP/ML估计，使用它可以模拟上述生成过程并创建人工数据。
• 对于参数θ的选择，给定观测值x，隐变量z的后验推断，即p(z|x;θ)，这对表示学习很有用。
• 对于参数θ的选择，变量x的边际推断，即p(x;θ)，这在需要先验x的情况下是有用的。

变分法

变分法是解决上一节提出的三个问题的关键。让我们从后验推理开始，即计算 p(z|x=𝐱⁽ⁱ⁾; θ)。我们可以通过应用贝叶斯定理和概率链式法则写出后验概率：

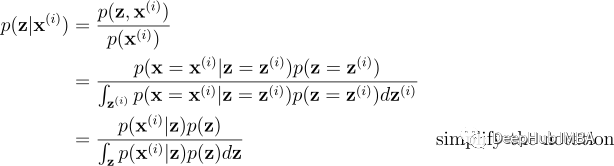
假设我们可以选择参数θ，因此先验分布p(z;θ)和似然p(𝐱⁽ⁱ⁾|z;θ)由生成过程定义的值是已知的。所以理论上后验p(z|𝐱⁽ⁱ⁾;θ)可以在计算分母中的积分后计算出来，这涉及到枚举不可观测变量z可能具有的所有可能值。

但是如果没有对 p(z|𝐱⁽ⁱ⁾; θ) 或 p(z; θ) 的任何简化假设，积分是难以处理的，这意味着任何用于评估积分的方法（包括枚举运算）的计算复杂度都是指数级的。

变分法就是为这种情况而设计的，它允许我们通过将统计推理问题转化为优化问题来避免棘手的积分问题。变分法提出了一个识别模型 q(z|𝐱⁽ⁱ⁾; ϕ) 作为真实后验 p(z|𝐱⁽ⁱ⁾; θ) 的近似值。通过最小化 q(z|𝐱⁽ⁱ⁾; ϕ) 和 p(z|𝐱⁽ⁱ⁾; θ) 之间的 KL 散度，我们可以解决后验推理问题。为了简化计算，这里将对识别模型和生成模型的参数 φ 和 θ 进行联合优化。

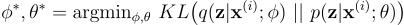
让我们对KL散度做进一步的推导，为简单起见，参数ϕ和θ将被省略。

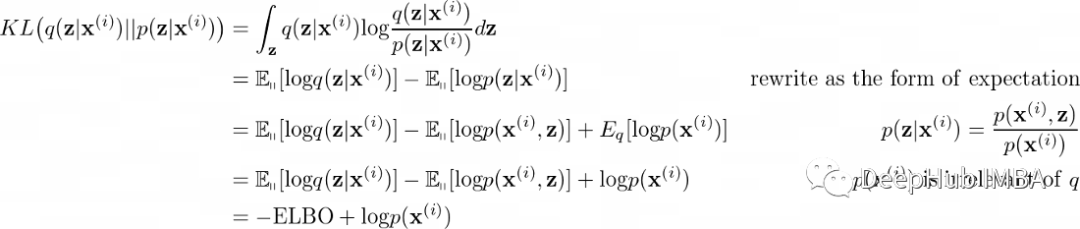
logp(x)是一个常数，所以在优化过程中可以忽略。我们还要重写ELBO:

优化问题现在等价于:

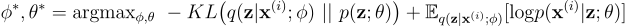
算法学习的过程

借助变分法可以避免复杂的积分，而下一个挑战是对给定的优化问题使用什么算法。如果能够解决这个问题那么上面提到的三个问题就都不是问题了。

就像其他深度学习模型一样，我们使用随机梯度下降进行优化，将要最大化的优化目标（即 ELBO）重写为要最小化的损失函数的形式：

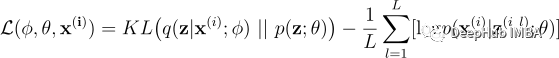
这里原始期望项使用蒙特卡洛方法进行近似，即对从 q(z|x⁽ⁱ⁾; ϕ) 中提取的 L 个样本 z⁽ⁱ ˡ⁾ 求平均 logp(x⁽ⁱ⁾|z; θ)。给定可微损失函数，VAE 的完整学习算法如下：

1. 得到由 M 个数据点组成的小批量；
2. 计算小批量损失 ∑ ℒ(ϕ,θ, x⁽ⁱ⁾) / M；
3. 计算梯度 ∑ ∇ℒ(ϕ,θ, x⁽ⁱ⁾) / M；
4. 应用梯度来更新参数 ϕ 和 θ；
5. 重复前 4 个步骤直到收敛。

在实际 应用中，样本 z⁽ⁱ ˡ⁾ 不是直接从 q(z|𝐱⁽ⁱ⁾; ϕ) 中抽取的，因为 q 可以是任意复杂的分布并且难以采样。为了提高采样效率，可以通过设置g(ϵ⁽ⁱ ˡ⁾, 𝐱⁽ⁱ⁾; ϕ)，其中g(*， *;ϕ)可以是任何以噪声ϵ⁽ⁱ ˡ⁾，而𝐱⁽ⁱ⁾是神经网络的输入。噪声ϵ⁽ⁱ ˡ⁾是从一些简单分布p()中采样的(例如高斯分布)。

除了采样效率之外，重新参数化技巧的另一个优点是它允许对 ϕ 和 θ 进行更好和更全面的优化。假设我们直接从 q(z|𝐱⁽ⁱ⁾;ϕ)中抽取样本，损失中 MC 估计项的梯度只会反向传播到采样的潜在变量 z⁽ⁱˡ⁾， 它的梯度 w.r.t ϕ 不会被计算，所以参数 θ 只能通过损失中的 KL 散度项来优化，这对于学习稳定性来说可能不是最优的。

VAE vs. AE

我们对VAE和AE进行比较，这样可以帮助我们从自编码理论的角度更好地理解VAE。

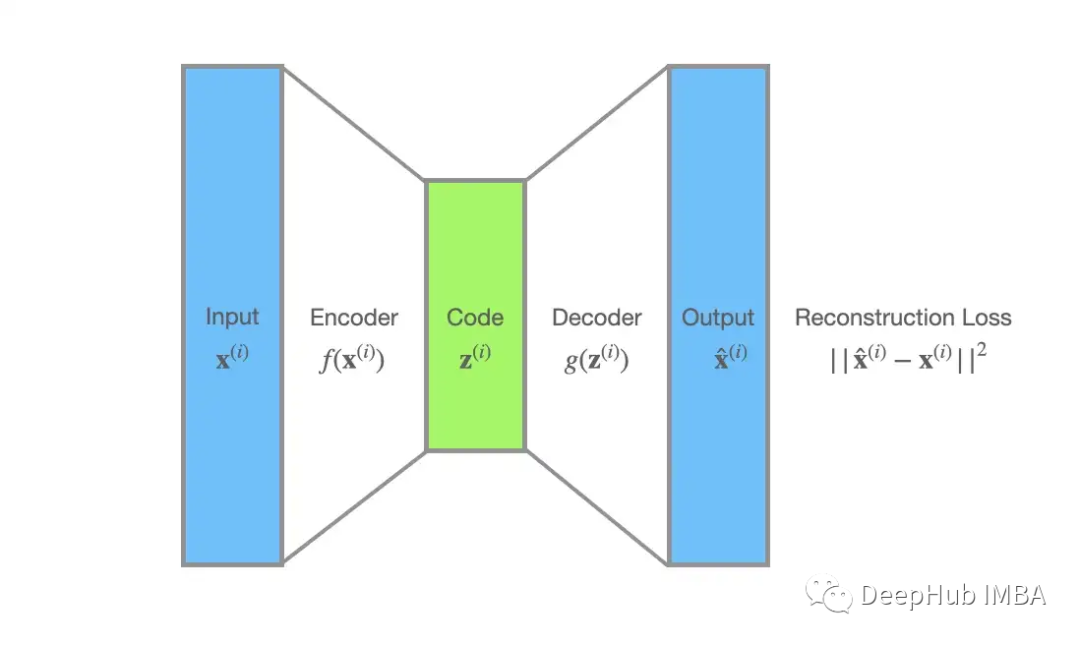
在自编码器的世界中，编码器f(x)处理数据点𝐱⁽ⁱ⁾，然后生成z⁽ⁱ⁾。解码器g(z)将z⁽ⁱ⁾作为输入，并重建的x̂⁽ⁱ⁾。自动编码器一般都是在重建损失ℒ(𝐱⁽ⁱ⁾)，平方误差，||x̂⁽ⁱ⁾ − x⁽ⁱ⁾||²下学习。

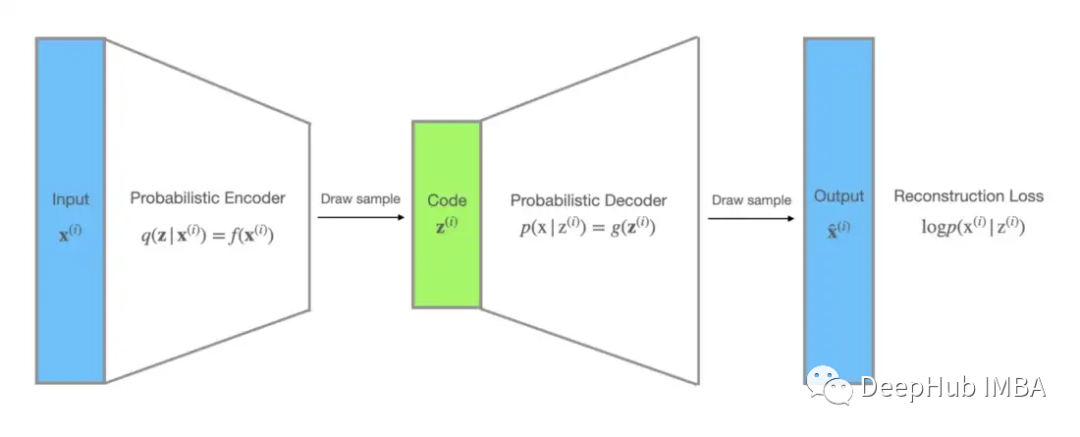
对于 VAE，未观察到的变量 z 可以解释为分布编码。识别模型 q(z|x; ϕ) 可以被视为概率编码器，因为给定数据点 x 它会产生 z 的可能值的分布，而p(x|z;θ)可以看作一个概率解码器：给定一个编码z，它产生x的可能对应值的分布。

VAE损失函数中的MC估计项恰好是负对数似然的形式，因此可以作为重建损失，损失函数中还包含一个 KL 散度项，它充当正则化项并强制分布 q(z|x; ϕ) 接近先验 p(z; θ)。

所以VAE 可以看作是 AE 的概率版本，它们都是表示学习的有用工具。而VAE 相对于 AE 的优势在于它明确地模拟了生成过程，并且能够通过从 p(x|z; θ) 中采样来生成类似于真实数据的人工数据点。更重要的是VAE 学习的分布在统计分析中非常有用。

使用MNIST的演示VAE

在所有的理论解释之后，我们使用MNIST图像重建任务的演示VAE。VAE模型的结构如下:

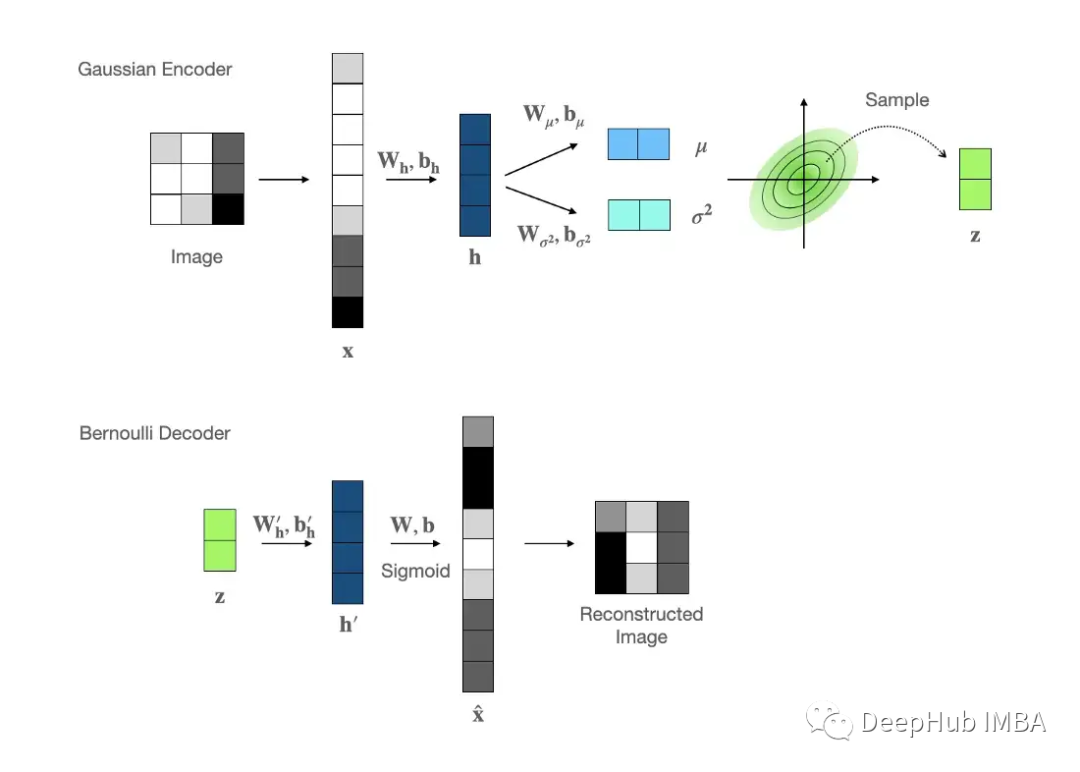
高斯编码器:由于其稳定的静态特性和简单的采样，我们选择多元高斯作为编码器输出分布，其中的均值和方差值由前馈网络建模。

伯努利解码器:MNIST数据是灰度图像，其中每个像素都可以表示为0到1之间的一个浮点数，因此伯努利分布是我们解码器的首选。Fσ是元素级sigmoid激活函数，公式如下:

损失函数:为简单起见，我们将先验p(z)设置为正态分布𝒩(0,I)。概率编码器的分布是𝒩(𝐳;𝛍，𝛔²𝐈)，其中μ∈ℝᴶ，σ²∈ℝ₊ᴶ和μⱼ，σ²分别是均值/向量的第j个分量。KL散度项为:

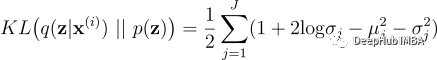
对于期望项，我们设置样本数L=1并使用MC估计logp(x⁽ⁱ⁾|z⁽ⁱ¹⁾)来代替原始期望项，其中代码z⁽ⁱ¹⁾通过重新参数化技巧进行采样。也就是说z⁽ⁱ ¹⁾=μ+σ⊙ϵ⁽ⁱ ¹⁾，噪声ϵ⁽ⁱ¹⁾从正态分布中采样𝒩(0, I), ϵ ∈ ℝᴶ,μ/σ²是编码器中的均值/向量。

结合KL和MC估计项可以得到完整的损失函数(负ELBO):

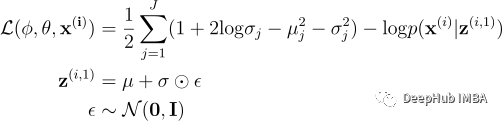
这是概率解码器 p(x|z; θ) 生成的手写数字图像的有趣可视化。

总结

总最后总结本文的关键要点:

• VAE用于解决3个统计问题，分别是参数估计、后验推断和边缘分布推断。
• 通过使用变分方法，可以构造一个损失函数为负ELBO的参数优化问题，通过重新参数化技巧和随机梯度下降算法来解决VAE的统计问题。
• 变分法引入的识别模型q(z|x; ϕ)和预定义的生成模型p(x|z; θ)分别对应概率编码器和解码器，而损失函数可以解释为组合重建损失以及正则项。

以上就是本文的所有内容，对于VAE的实现代码，请看这里：

https://avoid.overfit.cn/post/3da44e8799104455b554f40c3c04fef6

作者：JZ