2496. 数组中字符串的最大值
一个由字母和数字组成的字符串的 值 定义如下:
- 如果字符串 只 包含数字,那么值为该字符串在
10进制下的所表示的数字。 - 否则,值为字符串的 长度 。
给你一个字符串数组 strs ,每个字符串都只由字母和数字组成,请你返回 strs 中字符串的 最大值 。
提示:
1 <= strs.length <= 1001 <= strs[i].length <= 9strs[i]只包含小写英文字母和数字。
示例
输入:strs = ["alic3","bob","3","4","00000"]
输出:5
解释:
- "alic3" 包含字母和数字,所以值为长度 5 。
- "bob" 只包含字母,所以值为长度 3 。
- "3" 只包含数字,所以值为 3 。
- "4" 只包含数字,所以值为 4 。
- "00000" 只包含数字,所以值为 0 。
所以最大的值为 5 ,是字符串 "alic3" 的值。
思路
简单模拟即可
class Solution {
public:
int parse(string& s) {
bool isNum = true;
int num = 0;
for (int i = 0; i < s.size(); i++) {
if (s[i] >= '0' && s[i] <= '9') {
num = num * 10 + s[i] - '0';
} else {
isNum = false;
break;
}
}
return isNum ? num : s.size();
}
int maximumValue(vector<string>& strs) {
int ans = 0;
for (auto& s : strs) ans = max(ans, parse(s));
return ans;
}
};
2497. 图中最大星和
给你一个 n 个点的无向图,节点从 0 到 n - 1 编号。给你一个长度为 n 下标从 0 开始的整数数组 vals ,其中 vals[i] 表示第 i 个节点的值。
同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条双向边。
星图 是给定图中的一个子图,它包含一个中心节点和 0 个或更多个邻居。换言之,星图是给定图中一个边的子集,且这些边都有一个公共节点。
下图分别展示了有 3 个和 4 个邻居的星图,蓝色节点为中心节点。
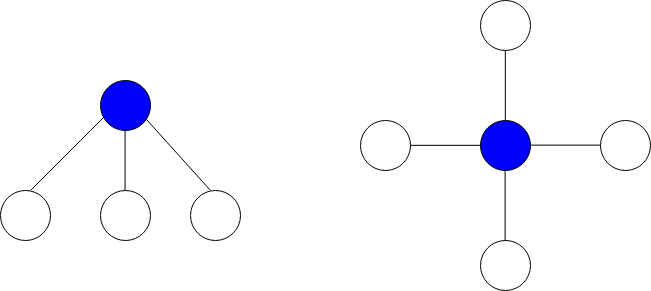
星和 定义为星图中所有节点值的和。
给你一个整数 k ,请你返回 至多 包含 k 条边的星图中的 最大星和 。
提示:
n == vals.length1 <= n <= 10^5-10^4 <= vals[i] <= 10^40 <= edges.length <= min(n * (n - 1) / 2``, 10^5)edges[i].length == 20 <= ai, bi <= n - 1ai != bi0 <= k <= n - 1
示例
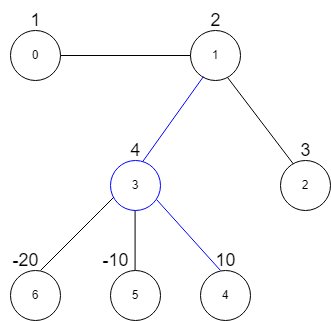
输入:vals = [1,2,3,4,10,-10,-20], edges = [[0,1],[1,2],[1,3],[3,4],[3,5],[3,6]], k = 2
输出:16
解释:上图展示了输入示例。
最大星和对应的星图在上图中用蓝色标出。中心节点是 3 ,星图中还包含邻居 1 和 4 。
无法得到一个和大于 16 且边数不超过 2 的星图。
思路
乍的一看以为是一道图论的题目。仔细审题后发现根本都不用建图。
首先,一个星图,需要包含一个中心点,以及0或多个邻接点。要求解的是最多包含k条边的最大星和。
也就是最多有k个邻接点。
那么只需要枚举一下以每个点作为中心点的星图即可。至于最多包含k个邻接点,选哪k个点呢?当然是vals最大的前k个点啦!注意,如果 vals为负数,纳入到星图里会使得星和变小。
所以,我们只需要维护一下每个点的所有邻接点,然后把邻接点按照vals值从大到小排序,然后以每个点作为中心点,取前k个vals值大于0的邻接点纳入到星图中即可。
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
class Solution {
public:
int maxStarSum(vector<int>& vals, vector<vector<int>>& edges, int k) {
int n = vals.size();
vector<vector<int>> f(n); // 存储某个点的全部邻接点
for (auto& e : edges) {
int a = e[0], b = e[1];
f[a].push_back(b);
f[b].push_back(a);
}
int ans = -1e4;
// 以每个点作为中心点, 尝试构造不超过k个边的最大星和
for (int i = 0; i < n; i++) {
int sum = vals[i]; // 中心点必须纳入
vector<int>& v = f[i];
// 将全部邻接点按照vals值从大到小排序
sort(v.begin(), v.end(), [&](int a, int b) {
return vals[a] > vals[b];
});
// 纳入前k个vals值大于0的点
// 由于是从大到小排好序, 当第一次遇到vals值等于0,便可以退出循环了
for (int j = 0; j < v.size() && j < k && vals[v[j]] > 0; j++) sum += vals[v[j]];
ans = max(ans, sum);
}
return ans;
}
};
看到其他大佬的代码,发现其实可以写的更为简短
class Solution {
public:
int maxStarSum(vector<int>& vals, vector<vector<int>>& edges, int k) {
vector<vector<int>> g(vals.size());
for (auto& e : edges) {
g[e[0]].push_back(vals[e[1]]); // 这里不插入邻接点, 而直接插入邻接点对应的vals
g[e[1]].push_back(vals[e[0]]);
}
int n = vals.size(), res = INT_MIN;
for (int i = 0; i < n; ++i) {
sort(g[i].rbegin(), g[i].rend()); // 从大到小排序, 可以直接取逆的迭代器
int temp = vals[i], t = k;
for (int v : g[i]) { // foreach循环很简洁
if (v > 0 && t--) temp += v; // 这里也写的比较
else break;
}
res = max(res, temp);
}
return res;
}
};
2498. 青蛙过河II
给你一个下标从 0 开始的整数数组 stones ,数组中的元素 严格递增 ,表示一条河中石头的位置。
一只青蛙一开始在第一块石头上,它想到达最后一块石头,然后回到第一块石头。同时每块石头 至多 到达 一次。
一次跳跃的 长度 是青蛙跳跃前和跳跃后所在两块石头之间的距离。
- 更正式的,如果青蛙从
stones[i]跳到stones[j],跳跃的长度为|stones[i] - stones[j]|。
一条路径的 代价 是这条路径里的 最大跳跃长度 。
请你返回这只青蛙的 最小代价 。
提示:
2 <= stones.length <= 10^50 <= stones[i] <= 10^9stones[0] == 0stones中的元素严格递增。
示例
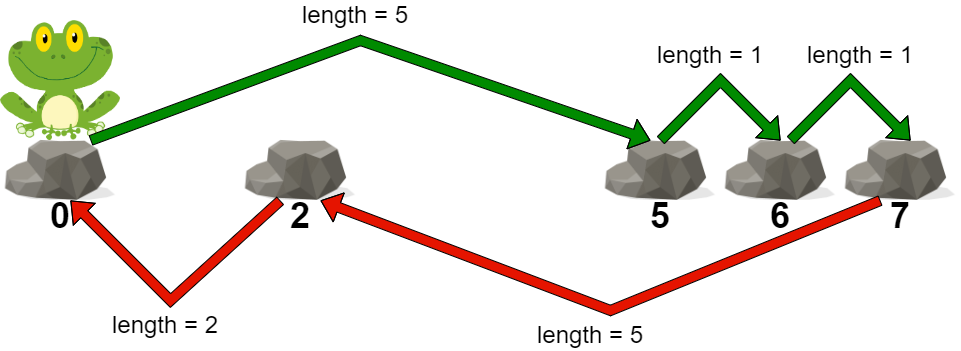
输入:stones = [0,2,5,6,7]
输出:5
解释:上图展示了一条最优路径。
这条路径的代价是 5 ,是这条路径中的最大跳跃长度。
无法得到一条代价小于 5 的路径,我们返回 5 。
思路
由于中间的每块石头最多只能到达一次,所以我们需要将全部石头分成两部分,一部分是去程中到达过的石头,另一部分是回程中到达过的石头。这里稍微停顿一下,有没有可能某个石头没有被到达过呢?
一定不会!假设某个石头x没有被到达过,则在去程中,一定需要从x左侧跳到x右侧,如果引入x这块石头,一定能使得这段跳跃的距离被拆成更小的2段。引入x一定不会使得答案变得更差。所以我们可以认为每块石头都被恰好到达过1次。
由于一条路径的代价是这条路径中的最大跳跃长度,我们要使得代价尽可能小,则每次跳跃尽可能要选择更近的石头。
可以先这样来考虑,假设只有去程,没有回程,那么很明显的,挨个石子地跳,就能使得最大跳跃长度最短。
现在需要加入去程,那么在去程的石子尽可能相邻的情况下,要挑出一些石子来留给回程。
接下来这样考虑,从起点的石头(下标为0)开始,去程的第一跳,我们要选择尽可能近的石头,不妨选择下标为1的石头;然后,镜像的考虑,回程的最后一跳,需要从某块石头跳到第0号石头,由于最近的1号石头已经被跳过了,那么回程的最后一跳最近的就只能选择2号石头。
容易想到,只有交替分配石头,即1号石头作为去程,2号作为回程,3号作为去程,4号作为回程,只有这样才能使得整个路径的最大跳跃长度最短。
// 110ms
class Solution {
public:
int maxJump(vector<int>& stones) {
int n = stones.size();
if (n == 2) return stones[1];
int ans = stones[1];
// 去程
for (int i = 3; i < n; i += 2) ans = max(ans, stones[i] - stones[i - 2]);
ans = max(ans, stones[2]);
// 回程
for (int i = 4; i < n; i += 2) ans = max(ans, stones[i] - stones[i - 2]);
return ans;
}
};
代码还可以简化
class Solution {
public:
int maxJump(vector<int>& stones) {
int ans = stones[1];
for (int i = 2; i < stones.size(); i++) ans = max(ans, stones[i] - stones[i - 2]);
return ans;
}
};
如果想不到这种贪心策略,也可以二分答案。因为最远距离是10^9,我们每次进行二分出一个值x,并判断是否能以不超过x作为最大跳跃距离,完成去程和回程,即可。二分总次数最多大概30次,每次判断能否完成往返程,需要遍历一次,总的时间复杂度最多是 30 × 10^5,大概在10^6级别。
// 330ms
class Solution {
public:
vector<bool> st;
// 能否以不超过limit完成往返程
bool check(vector<int>& stones, int limit) {
// printf("看%d是否能满足\n", limit);
int n = stones.size(), i = 0;
for (int j = 0; j < n; j++) st[j] = false;
// 先以最接近limit的跨度, 跳完去程
while (i < n - 1) {
// i是当前起跳的位置
// 需要在i + 1之后, 找到一个位置x, 使得他俩的距离恰好 <= limit
int l = i + 1, r = n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (stones[mid] - stones[i] <= limit) l = mid;
else r = mid - 1;
}
if (stones[l] - stones[i] > limit) return false; // 找不到这样一个点
// printf("去程跳%d\n", l);
st[l] = true; // 该点在去程中被跳过
i = l; // 更新下一个起跳点
}
// 验证返程, 挨个往最近的跳就行了
i = n - 1;
while (i > 0) {
// 跳到的点
int j = i - 1;
while (j > 0 && st[j]) j--;
if (stones[i] - stones[j] > limit) return false;
i = j;
}
return true;
}
int maxJump(vector<int>& stones) {
int n = stones.size();
st.resize(n);
int l = 0, r = stones[n - 1];
while (l < r) {
int mid = l + r >> 1;
if (check(stones, mid)) r = mid;
else l = mid + 1;
}
return l;
}
};
注意到,实际上,上面的二分过程中也包含了贪心的操作,去程中每次跳跃取了不超过limit的最大值,二分中套了二分。
2499. 让数组不相等的最小总代价
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,两者长度都为 n 。
每次操作中,你可以选择交换 nums1 中任意两个下标处的值。操作的 开销 为两个下标的 和 。
你的目标是对于所有的 0 <= i <= n - 1 ,都满足 nums1[i] != nums2[i] ,你可以进行 任意次 操作,请你返回达到这个目标的 最小 总代价。
请你返回让 nums1 和 nums2 满足上述条件的 最小总代价 ,如果无法达成目标,返回 -1 。
提示:
n == nums1.length == nums2.length1 <= n <= 10^51 <= nums1[i], nums2[i] <= n
示例
输入:nums1 = [1,2,3,4,5], nums2 = [1,2,3,4,5]
输出:10
解释:
实现目标的其中一种方法为:
- 交换下标为 0 和 3 的两个值,代价为 0 + 3 = 3 。现在 nums1 = [4,2,3,1,5] 。
- 交换下标为 1 和 2 的两个值,代价为 1 + 2 = 3 。现在 nums1 = [4,3,2,1,5] 。
- 交换下标为 0 和 4 的两个值,代价为 0 + 4 = 4 。现在 nums1 = [5,3,2,1,4] 。
最后,对于每个下标 i ,都有 nums1[i] != nums2[i] 。总代价为 10 。
还有别的交换值的方法,但是无法得到代价和小于 10 的方案。
思路
这是一道思维题,需要分类讨论。
首先,对于满足nums1[i] = nums2[i]的所有位置i。这些位置是一定要被交换的,这是确定的。而每个i是和另一个位置做交换,不确定的是这另一个位置。
我周赛当天只想到这里,后面就卡住,然后一通乱想,没有再进行下去了。
对于那些需要交换的位置i,我们可以按照元素大小分别进行统计计数。
比如
nums1: 1 1 2 2 2 3 5 4
nums2: 1 1 2 2 2 5 3 4
一共有5个位置的数需要交换,其中1有2个,2有3个。
关键的一步在于,要推出:
出现次数最多的数,如果其次数没有过半,则这些需要交换的位置,可以内部互相两两交换
现在我们只考虑,需要交换的那些位置。
可以这样想:如果某个数x出现了n次,那么只要其余的数至少也为n个,则其余的数一定是与x不同的,则全部的x一定可以被换掉(换一次也同时换掉了同等数量的其他的数)。同理,我们依次看每一个数,看这个数的出现次数,以及剩余的数的次数,只要剩余的数的次数之和大于等于这个数的次数,就一定能把这个数给全部换掉。
所以,只要出现次数最多的那个数,不超过总次数的一半,就一定能在内部通过两两互换进行解决。
这里还有另一个问题,由于每次互换是交换2个数。
-
如果总的次数是偶数,那么很明显,两两配对即可。总的代价就是全部需要交换的位置的下标之和。
-
如果总的次数是奇数,那么会多出一个可怜的单身汉,没人和他配对。此时这个单身汉需要和另外一个数额外做一次交换。
那么和哪个数做交换呢?肯定要和另外一个不等于这个数的数做交换才行。
实际我们可以证明,这个单身汉总是可以和下标为
0的数进行交换,从而使得额外的开销为0,总代价也是全部需要交换的位置的下标之和下面证明一下这个结论,设最后剩下的单身汉为
x(其实最后剩下的那个数我们可以自己任选):-
若下标为
0的数,在需要交换的位置当中,那么有nums1[0] = nums2[0],我们只需要让最后剩下的那单身汉不等于nums1[0]就好了 -
若下标为
0的数,不在需要交换的位置当中,那么有nums1[0] != nums2[0],那么最后剩下的单身汉不能为nums1[0],也不能为nums2[0]。这就要求数字的种类至少为3,能保证吗?答案是可以的。因为当总次数为奇数时,一定有至少3种不同的数字,恰好比2种多至少1种。(可以尝试下,总次数为奇数,无非就是1,3,5,…,但次数为1时,不满足出现次数最多的数不过半;当次数为3时,只能是3种数字各出现1次;次数为5同理;所以能得出,出现次数为奇数时,数字的种类数至少为3)
-
于是,通过上面的分类讨论,我们推导出了:当出现次数最多的数,不过半时,答案就是所有需要交换的数的下标之和。
那么当出现次数最多的数,过半了,会怎么样呢?
那就是,这个数字只有一部分能够被内部消化(与同样需要交换的那些位置进行交换)。多出来一部分,需要与那些不需要交换的位置进行交换,比如
nums1: 2 3 1 1 1 1 2 2 4
nums2: 3 2 1 1 1 1 2 2 5
需要交换的位置的总次数为6,其中1出现了4次,2出现了2次。
1的出现次数(4)过了半(3)。那么有2个1,可以和2进行交换;还剩2个1,需要和其他的位置进行交换。
我们只需要按照位置从小到大遍历一次数组,找到那些nums1[i] != nums2[i],并且nums1[i] != 1 && nums2[i] != 1的位置,来消耗掉多出的1的次数。
如果多出的1能够被消耗完,说明能够完成目标。否则不能。
class Solution {
public:
long long minimumTotalCost(vector<int>& nums1, vector<int>& nums2) {
// sameCnt 是nums1[i] = nums2[i] 的那些位置的个数
// majorCnt 是众数的出现次数
// majorNum 是众数的值
int sameCnt = 0, majorCnt = 0, majorNum = 0, n = nums1.size();
long long ans = 0;
unordered_map<int, int> freq;
for (int i = 0; i < n; i++) {
if (nums1[i] == nums2[i]) {
ans += i;
sameCnt++;
if (++freq[nums1[i]] > majorCnt) {
majorNum = nums1[i];
majorCnt = freq[nums1[i]];
}
}
}
// 众数的出现次数不过半, 则直接返回下标之和
if (majorCnt * 2 <= sameCnt) return ans;
// 否则, 看剩余的次数能不能被消耗完
int remainCnt = 2 * majorCnt - sameCnt;
for (int i = 0; i < n && remainCnt > 0; i++) {
if (nums1[i] != nums2[i] && nums1[i] != majorNum && nums2[i] != majorNum) {
ans += i;
remainCnt--;
}
}
return remainCnt == 0 ? ans : -1;
}
};
总结
T1是模拟;T2是遍历+排序;T3是贪心(也可以用二分);T4是思维题,需要分类讨论。

](https://img-blog.csdnimg.cn/img_convert/59c7bb6c00ed44529f87d41906bccfb1.png)