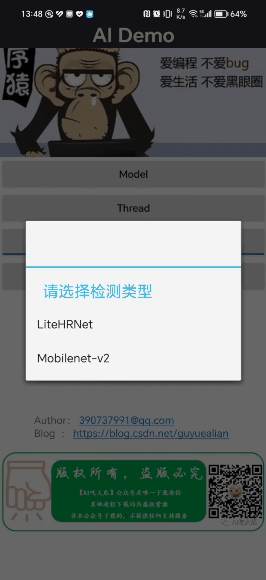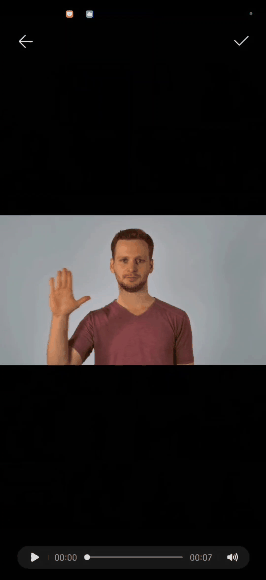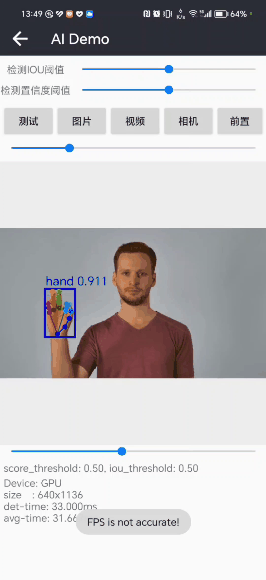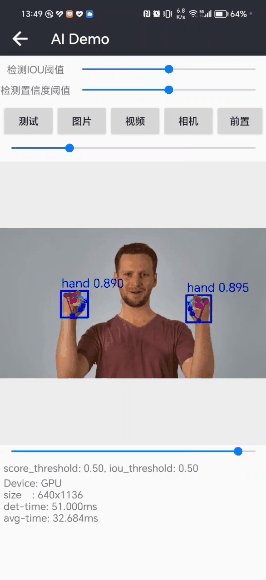
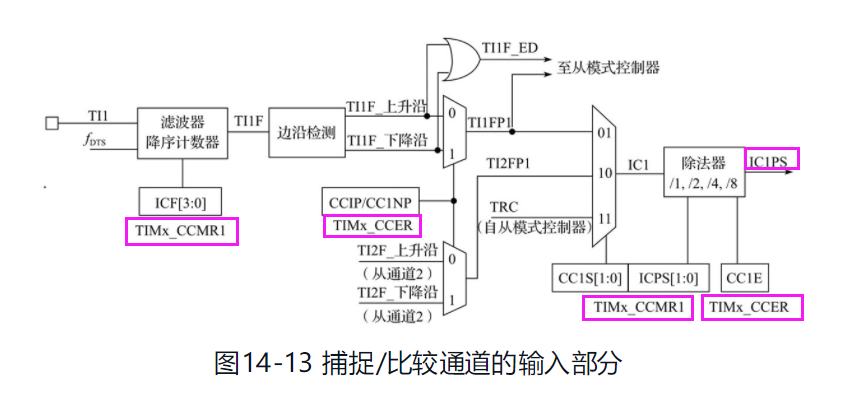
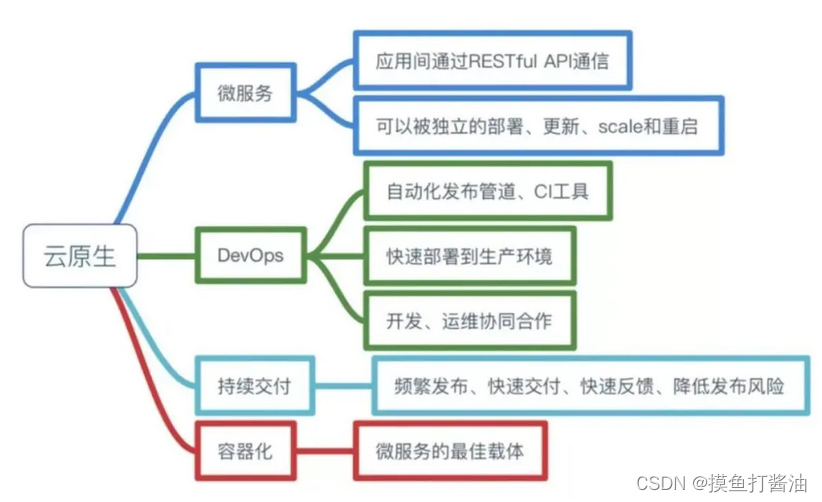
http://cplusoj.com/d/senior/p/SS231017C

感觉可以分治某个区间 $[l,r]$，且他们都是在下面 $k$ 已经选的基础上

然后肯定要枚举最大值，最大值越长越好

---

Hint 1

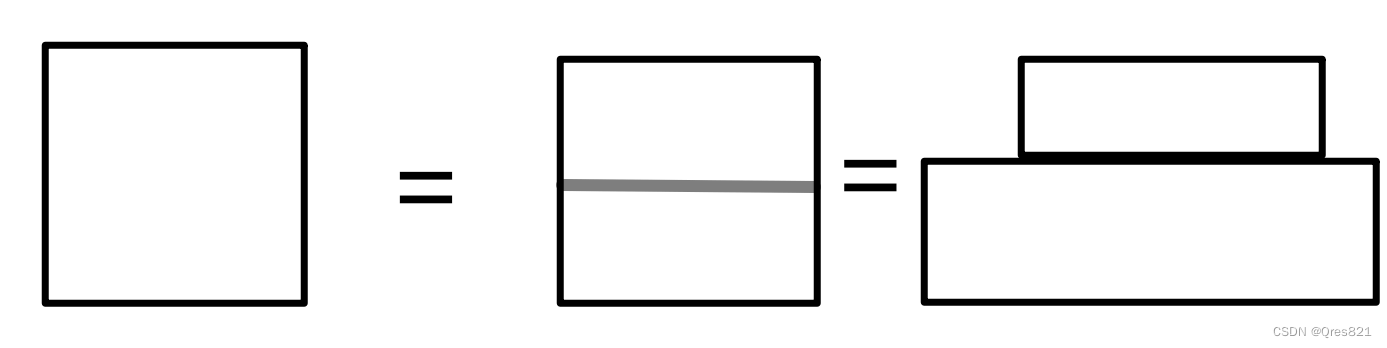
Hint 2

$f(l,r,k)$ 可以通过枚举 $mid$，或者枚举 $k^{\prime }$ 进行暴力转移

---

根据Hint1，我们区间最大如果选则必然是选整个区间，高度是最小值，然后往最小值两边递归

同理，如果最大值不选则是往最大值两边递归

这是一个按最大最小分治的过程，可以通过记忆化来优化

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 3010
//#define M
//#define mo
struct Num {
	int x, id; 
}mx[N][22], mn[N][22];
int n, m, i, j, k, T;
int a[N], Log2[N]; 
map<pair<int, int>, int>f[N]; 

Num max(Num a, Num b) {
	return (a.x>b.x ? a : b); 
}

Num min(Num a, Num b) {
	return (a.x<b.x ? a : b); 
}


Num Mx(int l, int r) {
	int k = Log2[r-l+1]; 
	return max(mx[l][k], mx[r-(1<<k)+1][k]); 
}

Num Mn(int l, int r) {
	int k = Log2[r-l+1]; 
	return min(mn[l][k], mn[r-(1<<k)+1][k]); 
}

int S(int r, int n) { // 末项、公差 
	int l = r - n + 1; 
	return (l+r)*n/2; 
}

int dfs(int l, int r, int k) {
	if(l>r) return 0; 
	if(f[l].find({r, k})!=f[l].end()) return f[l][{r, k}]; 
	Num x, y; x=Mx(l, r); y=Mn(l, r); 
	int ans=1e18; 
//	printf("%lld %lld\n", x.id, y.id); 
	ans=min(ans, a[x.id]-k+dfs(l, x.id-1, k)+dfs(x.id+1, r, k)); 
	ans=min(ans, S(a[x.id]-k, a[y.id]-k)+dfs(l, y.id-1, a[y.id])+dfs(y.id+1, r, a[y.id])); 
	return f[l][{r, k}]=ans; 
}

signed main()
{
///	freopen("in.txt", "r", stdin);
//	freopen("out.txt", "w", stdout);
	freopen("cake.in","r",stdin);
	freopen("cake.out","w",stdout);
//	T=read();
//	while(T--) {
// 
//	}
	n=read(); 
	for(i=1; i<=n; ++i) a[i]=read();
	for(i=1; i<=n; ++i) mx[i][0].x=a[i], mx[i][0].id=i; 
	for(i=1; i<=n; ++i) mn[i][0].x=a[i], mn[i][0].id=i; 
	for(i=2; i<=n; ++i) Log2[i]=Log2[i>>1]+1; 
	for(k=1; k<=20; ++k)
		for(i=1, j=(1<<k-1)+1; i+(1<<k)-1<=n; ++i, ++j)
			mx[i][k]=max(mx[i][k-1], mx[j][k-1]), 
			mn[i][k]=min(mn[i][k-1], mn[j][k-1]); 
	printf("%lld", dfs(1, n, 0)); 
	return 0;
}