本文为🔗小白入门Pytorch内部限免文章
- 🍨 本文为🔗小白入门Pytorch中的学习记录博客
- 🍦 参考文章:【小白入门Pytorch】教案二
- 🍖 原作者:K同学啊
目录
- 一、神经网络的组成部分
- 1. 神经元
- 2. 神经网络层
- 3. 损失函数
- 4. 优化器
- 二、PyTorch中的层
- 1. 全连接层
- 2. 卷积层
- 3. 池化层
- 4. 循环神经网络层
- 5. 转置卷积层
- 6. 归一化层
- 7. 激活函数层
- 三、数据加载与预处理
- 1. 数据加载
- 🚩Dataset
- 🚩DataLoader
- 2. 数据预处理
- 🚩Tensor转换
- 🚩数据变换
- 🚩数据标准化
- 🚩图像增强
- 四、模型训练与验证
- 1. 模型训练
- 2. 模型验证
- 闯关练习
一、神经网络的组成部分
在第一部分中我们了解了 Pytorch 的相关基础知识,在这一篇文章中我将使用 Pytorch 进入深度学习的学习,学习如果使用 Pytorch 搭建神经网络中的一些基础代码,具体讲包含如下内容:
- 神经网络的组成部分
- 神经元
- 神经网络层
- 如何使用 Pytorch 完成数据加载工作以及相应的数据预处理
- 训练神经网络模型并验证
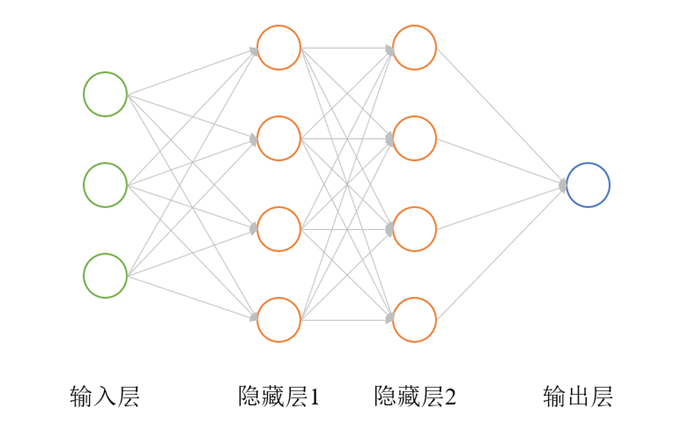
神经网络是一种由多个神经元以一定的方式联结形成的网络结构,是一种仿照生物神经系统结构和功能的人工智能技术。神经网络通常由输入层、输出层和若干个隐藏层组成,每个层包含若干个神经元。
神经网络的基本组成单位是神经元,它模拟了生物神经元的行为特征,包括输入信号的接收、加权求和、非线性激活等过程。神经元接收来自前一层神经元的输入信号,将输入信号进行加权求和,并通过激活函数将结果转换为输出信号,并将输出信号传递给下一层神经元。如图1所示为一个经典的以全连接(Full Connected, FC)方式形成的神经网络,每个圆圈代表一个神经元,圆圈间的连线代表神经元之间的联结。
1. 神经元
神经生物学家Warren MeCulloch和数学家Walter Pitts于1943年提出了一种基于早期的神经元理论学说的人工神经网络模型,称为MP模型(McCulloch-Pitts模型)。该模型是一种具有生物神经元特征的人工神经网络模型,被认为是神经网络研究的开端。
MP模型的基本思想是将神经元视为一个二进制变量,其输出值只能为0或1。神经元接收来自其他神经元的输入信号,通过一个阈值函数对输入信号进行加权和处理,并产生一个二进制输出值。MP模型中的神经元只有两种状态,即兴奋态(输出值为1)和抑制态(输出值为0),通过神经元之间的连接,可以实现复杂的计算功能。MP模型的主要贡献在于将生物神经元的工作原理转化为数学模型,为后续的神经网络研究奠定了基础。虽然MP模型非常简单,但它的基本思想和理论对于神经网络的发展和应用具有重要意义,为人工智能和机器学习的发展奠定了基础。如图2所示为MP神经元模型。
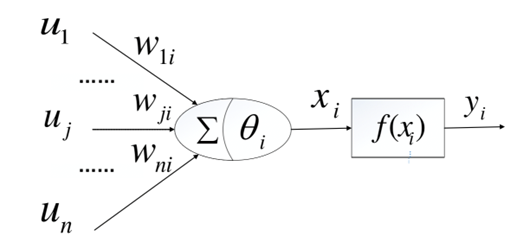
如上图所示, u 1 , . . . . . . u j , . . . . . . u n u_1, ......u_j, ......u_n u1,......uj,......un是一个 n n n维向量,代表与第 i i i个神经元相连接的其他神经元传递的信号; w 1 i , . . . . . , w j i , . . . . . . w n i w_{1i}, ....., w_{ji}, ......w_{ni} w1i,.....,wji,......wni分别代表其他神经元和第 i i i个神经元之间连接的权重值;代表第 i i i个神经元的阈值; x i x_i xi则称为第 i i i个神经元的输入,可表示为如式1所示; f ( x i ) f(x_i) f(xi)是非线性函数,如式2所示。
KaTeX parse error: \tag works only in display equations
KaTeX parse error: \tag works only in display equations
神经元通常由以下几个部分组成:
- **输入(Inputs):**神经元接收来自其他神经元或外部环境的输入数据。
- **权重(Weights):**每个输入都与一个权重相关联,用于调整输入的重要性。
- **激活函数:**激活函数将加权输入映射到输出。常用的激活函数包括Sigmoid、ReLU和Tanh等。
- **偏差(Bias):**偏差是一个可学习的参数,用于调整神经元输出的阈值。
以下代码是一个简单的神经元模型,用 PyTorch 构建。让我解释一下这个模型的结构和功能:
- Neuron 类:是一个继承自 torch.nn.Module 的自定义神经元模型。继承自 torch.nn.Module 的基类允许你定义具有可学习参数的自定义神经网络模型。
- init 方法:这是模型的构造函数,它接受一个参数 input_size,表示输入特征的数量。在这个方法中,模型初始化了两个可学习的参数:weights 和 bias,这两个参数都被包装成 torch.nn.Parameter 对象,以便在模型的训练过程中进行优化。
- weights 是一个形状为 (input_size,) 的可学习权重向量,它与输入特征进行点乘。
- bias 是一个标量值,它用于调整模型的输出。
- forward 方法:这是模型的前向传播方法。在前向传播过程中,输入 inputs 与权重 weights 进行点乘,然后将点乘结果与 bias 相加,得到加权和 weighted_sum。然后,通过 sigmoid 激活函数对加权和进行激活,将结果作为模型的输出返回。
这个神经元模型可以用于二分类问题,其中 input_size 表示输入特征的数量,模型通过学习适当的权重和偏置来进行二元分类。在训练过程中,你可以使用标准的 PyTorch 优化器和损失函数来训练这个模型,以便它能够适应你的分类任务。
import torch
class Neuron(torch.nn.Module):
def __init__(self, input_size):
super(Neuron, self).__init__()
# 定义可学习的权重参数,形状为 (input_size,),与输入特征数量相对应
self.weights = torch.nn.Parameter(torch.randn(input_size))
# 定义可学习的偏置参数,初始化为随机值,标量
self.bias = torch.nn.Parameter(torch.randn(1))
def forward(self, inputs):
# 计算加权和:点乘输入和权重,然后加上偏置
weighted_sum = torch.sum(inputs * self.weights) + self.bias
# 应用 sigmoid 激活函数,将结果压缩到 [0, 1] 范围内
output = torch.sigmoid(weighted_sum)
return output
# 创建一个具有3个输入的神经元
neuron = Neuron(3) # 实际使用中,避免在代码中硬编码数值,这样可以使你的代码更具灵活性和可重用性。
# 输入数据
inputs = torch.tensor([0.5, -0.3, 0.1])# 实际使用中,避免在代码中硬编码数值,这样可以使你的代码更具灵活性和可重用性。
# 计算输出
output = neuron(inputs)
print(output)
tensor([0.5041], grad_fn=<SigmoidBackward>)
C:\Users\chengyuanting\.conda\envs\pytorch_cpu\lib\site-packages\tqdm\auto.py:22: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
对于上述代码,以下是一些初学者在未来学习和使用中应特别注意的点:
-
模块继承:当你创建自己的自定义神经网络层或模型时,确保从
torch.nn.Module继承,并调用它的初始化方法super().__init__()。 -
权重和偏置初始化:在实际应用中,随机初始化权重和偏置可能不是最佳选择。根据不同的激活函数和网络结构,有许多推荐的初始化方法,如Xavier初始化或He初始化。
-
使用torch.nn.Parameter:当你希望一个张量在训练过程中被优化时,你需要将它转化为
torch.nn.Parameter。这样,当你调用backward()方法进行反向传播时,PyTorch会自动计算这些参数的梯度。 -
计算加权和:在代码中,加权和是通过对输入和权重进行点乘然后加上偏置来计算的。在实践中,为了加速计算和处理大批量数据,通常使用矩阵乘法。
-
激活函数:此代码使用了sigmoid激活函数。在深度学习中,尤其是在深层网络中,ReLU激活函数和它的变种(如LeakyReLU、PReLU等)更为常见,因为它们可以帮助缓解梯度消失问题。
-
输入数据检查:在真实场景中,你可能需要检查输入数据的形状和类型,以确保它们与期望的输入匹配。
-
模型评估和训练模式:
torch.nn.Module有两种模式:训练模式和评估模式。你可以使用.train()和.eval()方法来切换它们。这在使用如Dropout和BatchNorm这样的层时非常重要。 -
硬编码数值:避免在代码中硬编码数值,如神经元的输入大小
3。这样可以使你的代码更具灵活性和可重用性。 -
GPU加速:如果你有一个支持CUDA的GPU,你可以将模型和数据移动到GPU上以加速计算。使用
.to('cuda')方法可以轻松实现这一点。 -
学习率和优化器:虽然此代码没有涉及训练过程,但在实际应用中,选择合适的学习率和优化器(如Adam、SGD等)是至关重要的。
2. 神经网络层
神经网络由多个神经元层组成。每一层都由许多神经元组成,并且通常具有相同的结构和激活函数。以下是一些常见的神经网络层类型:
- 全连接层(Fully Connected Layer):每个神经元都与前一层的所有神经元相连接。
- 卷积层(Convolutional Layer):应用卷积操作来提取输入数据中的空间特征。
- 池化层(Pooling Layer):通过减少特征图的大小来降低计算量,并保留重要的特征。
- 循环层(Recurrent Layer):通过在神经网络中引入时间维度来处理序列数据。
以下是一个包含两个全连接层的神经网络示例代码:
import torch
# 定义神经网络类,继承自 torch.nn.Module
class NeuralNetwork(torch.nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(NeuralNetwork, self).__init__()
# 定义第一个全连接层,输入大小为 input_size,输出大小为 hidden_size
self.fc1 = torch.nn.Linear(input_size, hidden_size)
# 定义第二个全连接层,输入大小为 hidden_size,输出大小为 output_size
self.fc2 = torch.nn.Linear(hidden_size, output_size)
def forward(self, inputs):
# 使用 ReLU 激活函数计算第一个全连接层的输出
hidden = torch.relu(self.fc1(inputs))
# 使用 sigmoid 激活函数计算第二个全连接层的输出,最终的模型输出
output = torch.sigmoid(self.fc2(hidden))
return output
# 创建一个具有2个输入、3个隐藏神经元和1个输出的神经网络
net = NeuralNetwork(2, 3, 1)
# 输入数据
inputs = torch.tensor([0.5, -0.3])
# 计算输出
output = net(inputs)
print(output)
tensor([0.4996], grad_fn=<SigmoidBackward>)
对于上述神经网络代码,以下是初学者在未来学习和使用中应特别注意的点:
-
模块继承:确保自定义神经网络模型从
torch.nn.Module继承,并在构造函数中调用super()。 -
权重初始化:PyTorch 的
torch.nn.Linear层会自动进行权重和偏置的初始化。但在某些情况下,你可能想使用特定的初始化策略,如 Xavier 或 He 初始化。 -
激活函数的选择:这里使用了 ReLU 和 sigmoid。ReLU 通常在隐藏层中使用,因为它有助于缓解梯度消失问题。Sigmoid 主要用于输出层,特别是在二分类问题中。但根据任务的不同,你可能需要使用其他激活函数。
-
模型结构:这是一个简单的两层全连接网络。随着深度学习的深入,你可能会遇到更复杂的网络结构,如卷积神经网络、递归神经网络等。
-
模型复杂性:选择合适的隐藏层大小和层数非常重要。过于复杂的模型可能会导致过拟合,而太简单的模型可能会导致欠拟合。
-
数据的形状:确保输入数据的形状与模型期望的形状匹配。这在处理更复杂的数据结构时尤为重要。
-
模型评估和训练模式:记住使用
.train()和.eval()方法在训练和评估模式之间切换模型,特别是当你使用如 Dropout 或 BatchNorm 这样的层时。 -
学习率和优化器:虽然此代码没有包含训练逻辑,但选择合适的学习率和优化器对于模型的训练非常关键。
-
GPU 加速:如果可用,考虑将模型和数据移到 GPU 以加速计算。
-
批处理:在真实应用中,我们通常不会一次只向模型提供一个样本。为了加速训练并利用 GPU 的并行计算能力,我们通常会使用批处理。
-
损失函数:为了训练神经网络,你还需要定义一个损失函数来衡量模型的性能。选择合适的损失函数是非常重要的。
3. 损失函数
神经网络的目标是最小化预测输出与真实标签之间的差异。损失函数衡量了这种差异,并提供一个可优化的目标。常见的损失函数包括均方误差(Mean Squared Error)、交叉熵损失(Cross-Entropy Loss)等。
- 均方误差(Mean Squared Error,MSE):计算预测值与目标值之间的平方差的平均值。
- 交叉熵损失(Cross-Entropy Loss):在分类问题中,计算预测概率分布与真实标签之间的交叉熵。
以下是一个使用均方误差作为损失函数的示例:
import torch
# 随机生成一些示例数据
predictions = torch.tensor([0.9, 0.2, 0.1])
labels = torch.tensor([1.0, 0.0, 0.0])
# 计算均方误差损失
loss_function = torch.nn.MSELoss()
loss = loss_function(predictions, labels)
print(loss)
tensor(0.0200)
4. 优化器
优化器用于更新神经网络的参数以最小化损失函数。它使用梯度下降算法来调整参数的值。常见的优化器包括随机梯度下降(Stochastic Gradient Descent,SGD)、Adam等。
以下是一个使用Adam优化器进行参数更新的示例:
import torch
# 创建一个神经网络和损失函数
net = NeuralNetwork(2, 3, 1) # 使用前面定义的 NeuralNetwork 类创建了一个神经网络实例。
loss_function = torch.nn.MSELoss() # 使用均方误差损失 (torch.nn.MSELoss()) 作为损失函数。
# 创建一个Adam优化器
optimizer = torch.optim.Adam(net.parameters(), lr=0.01) # 创建了一个 Adam 优化器,将网络的参数 (net.parameters()) 传递给它,并设置学习率为 0.01。
# 输入数据和真实标签
inputs = torch.tensor([0.5, -0.3])
labels = torch.tensor([1.0])
# 前向传播
output = net(inputs)
loss = loss_function(output, labels)
# 反向传播和参数更新
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(loss)
tensor(0.1930, grad_fn=<MseLossBackward>)
这个损失值是网络当前输出与给定标签之间的均方误差。在实际应用中,为了训练模型,你通常会对整个训练数据集重复这些步骤多次(称为多个“epoch”)。每次迭代都会调整模型的权重,以减少预测和真实标签之间的差异。
通过理解和应用这些神经网络的组成部分,您将能够构建和训练自己的深度学习模型。
二、PyTorch中的层
在PyTorch中,神经网络层(Layers)是神经网络的基本组成部分,用于对输入数据进行转换和提取特征。PyTorch提供了丰富的层类型和功能,使得构建和训练深度学习模型变得更加便捷和灵活。这里将介绍PyTorch中的一些常用层,并提供示例代码来帮助读者理解和学习。
目录
- 全连接层(Fully Connected Layer)
- 卷积层(Convolutional Layer)
- 池化层(Pooling Layer)
- 循环神经网络层(Recurrent Neural Network Layer)
- 转置卷积层(Transpose Convolutional Layer)
- 归一化层(Normalization Layer)
- 激活函数层(Activation Function Layer)
- 损失函数层(Loss Function Layer)
- 优化器层(Optimizer Layer)
1. 全连接层
全连接层,也被称为线性层或密集层,是最简单的神经网络层之一。它将输入的每个元素与权重相乘,并加上偏置项,然后通过激活函数进行非线性变换。全连接层的输出形状由其输入形状和输出维度确定。
下面是一个创建全连接层的示例代码:
import torch
import torch.nn as nn
# 定义输入和输出维度
input_size = 784
output_size = 10
# 创建全连接层
fc_layer = nn.Linear(input_size, output_size)
# 打印全连接层的权重和偏置项
print("权重:", fc_layer.weight)
print("偏置项:", fc_layer.bias)
权重: Parameter containing:
tensor([[ 0.0160, 0.0062, -0.0287, ..., 0.0215, 0.0108, -0.0172],
[-0.0318, -0.0062, -0.0220, ..., 0.0127, 0.0219, -0.0339],
[-0.0321, -0.0275, 0.0026, ..., 0.0116, -0.0345, -0.0314],
...,
[-0.0119, -0.0284, -0.0337, ..., -0.0189, -0.0109, -0.0295],
[-0.0185, 0.0307, 0.0045, ..., -0.0274, 0.0092, 0.0191],
[ 0.0159, -0.0178, -0.0089, ..., 0.0354, 0.0104, -0.0032]],
requires_grad=True)
偏置项: Parameter containing:
tensor([-0.0107, 0.0350, 0.0356, 0.0243, 0.0297, -0.0348, -0.0037, -0.0139,
-0.0057, -0.0108], requires_grad=True)
import torch
import torch.nn as nn
# 定义输入和输出维度
input_size = 784
output_size = 10
# 创建全连接层
fc_layer = nn.Linear(input_size,output_size)
# 打印全连接层的权重和偏置项
print("权重:",fc_layer.weight)
print("偏置项:",fc_layer.bias)
权重: Parameter containing:
tensor([[ 0.0171, -0.0287, 0.0152, ..., -0.0086, -0.0129, 0.0188],
[-0.0233, -0.0021, -0.0338, ..., 0.0245, -0.0078, 0.0107],
[-0.0333, -0.0065, -0.0221, ..., -0.0346, 0.0017, -0.0132],
...,
[ 0.0035, 0.0080, 0.0355, ..., 0.0192, -0.0175, 0.0022],
[ 0.0257, 0.0099, 0.0297, ..., 0.0120, 0.0195, 0.0294],
[ 0.0231, 0.0193, -0.0057, ..., -0.0346, -0.0151, -0.0046]],
requires_grad=True)
偏置项: Parameter containing:
tensor([-0.0103, -0.0124, -0.0269, -0.0132, -0.0227, 0.0169, -0.0310, -0.0185,
-0.0081, -0.0120], requires_grad=True)
这段代码创建了一个全连接层 (torch.nn.Linear),它接受一个大小为 784 的输入并产生一个大小为 10 的输出。这样的配置常常用于处理 28x28 的图像(例如 MNIST 手写数字数据集中的图像),其中每个图像有 784 个像素值,并且输出有 10 个类别(数字 0 到 9)。
提问:上述代码指定了输入和输出的形状,为什么权重和偏置也有输出值呢?
回答:是的,你只指定了输入和输出的形状。权重和偏置的初始值是通过torch.nn.Linear层的默认初始化策略自动设置的。
具体来说,torch.nn.Linear层的默认初始化策略是:
-
权重 (Weights):根据权重的维度随机初始化。使用的是均匀分布 U ( − k , k ) \text{U}(-\sqrt{k}, \sqrt{k}) U(−k,k),其中 k = 1 输入维度 k = \frac{1}{\text{输入维度}} k=输入维度1。这种初始化方法基于这篇论文。
-
偏置 (Biases):全部初始化为 0。
这些默认的初始化策略是为了确保网络在训练开始时具有合适的权重和偏置值分布,从而有助于更稳定和更快速的训练。当然,PyTorch 也允许你使用自定义的初始化策略,如果你有特定的需求或想尝试其他方法。
2. 卷积层
卷积层是卷积神经网络中的核心层之一,用于从输入数据中提取空间特征。卷积层通过滑动窗口(卷积核)在输入上进行局部感知,并输出对应的特征图。PyTorch中的卷积层包括二维卷积层和三维卷积层,分别用于处理二维和三维数据。
下面是一个创建二维卷积层的示例代码:
import torch
import torch.nn as nn
# 定义输入通道数、输出通道数和卷积核大小
in_channels = 3
out_channels = 16
kernel_size = 3
# 创建二维卷积层
conv_layer = nn.Conv2d(in_channels, out_channels, kernel_size)
# 打印二维卷积层的权重和偏置项
print("权重:", conv_layer.weight)
print("偏置项:", conv_layer.bias)
权重: Parameter containing:
tensor([[[[ 0.0702, -0.1437, -0.1326],
[-0.0973, 0.0009, -0.1629],
[-0.1632, 0.1558, -0.1518]],
[[ 0.0387, 0.0559, -0.1302],
[ 0.0991, 0.0028, -0.0975],
[ 0.1882, 0.1475, 0.1742]],
[[ 0.1917, 0.0549, -0.1678],
[-0.1780, 0.1637, -0.0897],
[-0.0097, -0.1158, 0.1518]]],
[[[ 0.1799, -0.1694, 0.0881],
[ 0.0683, -0.1335, 0.1891],
[-0.0664, 0.0099, -0.0451]],
[[-0.1918, 0.1088, -0.1077],
[ 0.0256, -0.1431, 0.0176],
[-0.1653, -0.1450, -0.0667]],
[[-0.0762, -0.1408, 0.1166],
[-0.0256, -0.0282, 0.1219],
[ 0.0909, -0.0737, 0.1692]]],
[[[-0.0439, -0.1325, -0.0611],
[ 0.0309, 0.1011, 0.1902],
[ 0.1622, -0.1850, 0.1716]],
[[-0.1499, -0.1466, 0.1856],
[-0.1687, 0.0206, -0.0860],
[-0.1424, 0.0386, -0.1480]],
[[-0.0194, 0.0740, -0.1510],
[ 0.0116, 0.0549, 0.1746],
[-0.1145, 0.1390, 0.1319]]],
[[[ 0.1043, 0.0242, -0.1910],
[-0.1051, -0.1808, 0.0374],
[ 0.1781, -0.1858, 0.0060]],
[[-0.0934, -0.1339, -0.0666],
[-0.0286, -0.1805, -0.1378],
[ 0.1206, 0.1755, 0.0045]],
[[ 0.1346, -0.0178, 0.0321],
[ 0.0446, 0.1757, -0.0183],
[-0.0257, -0.0324, -0.0763]]],
[[[ 0.0590, -0.0940, -0.1875],
[-0.1255, -0.0593, 0.0657],
[-0.0509, 0.1689, -0.1663]],
[[-0.1119, 0.0838, 0.1267],
[ 0.1769, 0.0408, -0.1839],
[ 0.0490, -0.0271, 0.0318]],
[[ 0.1104, -0.0362, 0.0687],
[-0.0150, 0.0155, -0.0989],
[-0.1325, -0.0640, -0.0575]]],
[[[-0.1241, 0.1122, 0.0775],
[-0.0040, -0.1418, -0.0271],
[ 0.0389, 0.0658, 0.1902]],
[[-0.0499, -0.0906, 0.0434],
[ 0.1280, 0.0496, 0.0029],
[-0.0455, 0.0738, -0.1049]],
[[ 0.1705, -0.0031, 0.0350],
[ 0.0448, 0.0148, 0.0772],
[-0.0615, -0.0372, -0.1793]]],
[[[-0.1294, 0.1765, 0.1309],
[ 0.0649, -0.1731, -0.1126],
[-0.1682, 0.1400, -0.1538]],
[[-0.1219, -0.0639, 0.1223],
[ 0.1202, -0.1885, 0.1660],
[ 0.0639, -0.0741, 0.1149]],
[[-0.0809, -0.1771, 0.1510],
[-0.0697, -0.1361, -0.1445],
[-0.1228, -0.1276, 0.0052]]],
[[[-0.0302, 0.0140, 0.0883],
[-0.0490, 0.1449, 0.0586],
[ 0.1588, -0.0526, -0.1503]],
[[-0.0502, 0.0160, 0.0381],
[-0.1263, -0.0991, 0.0144],
[ 0.0750, -0.1631, -0.1422]],
[[-0.1666, 0.0923, -0.1673],
[-0.0758, -0.1602, -0.0491],
[-0.0020, 0.0092, -0.0007]]],
[[[-0.1176, 0.0138, 0.0091],
[ 0.1686, -0.1003, -0.1847],
[-0.0492, 0.1492, -0.1031]],
[[-0.1093, -0.0982, -0.1551],
[ 0.1704, 0.0216, 0.0707],
[ 0.0386, -0.1707, -0.0408]],
[[-0.1419, -0.1824, -0.0584],
[-0.1812, 0.1770, -0.1561],
[-0.0807, -0.0485, -0.0218]]],
[[[ 0.0644, 0.1920, 0.1515],
[-0.1057, -0.0340, 0.0482],
[-0.1485, 0.1006, 0.1586]],
[[-0.0506, -0.0795, -0.0984],
[-0.1269, 0.0942, -0.1474],
[ 0.0718, 0.0926, 0.1824]],
[[ 0.1365, -0.1866, 0.1286],
[ 0.0838, 0.1178, 0.0186],
[ 0.0232, 0.1207, 0.1361]]],
[[[ 0.0588, 0.1733, 0.1763],
[ 0.1229, -0.1537, -0.1691],
[-0.0334, -0.0225, -0.0833]],
[[-0.0259, -0.0029, 0.1534],
[-0.1361, 0.0398, 0.1154],
[ 0.0483, -0.1365, 0.1029]],
[[-0.1727, -0.0605, -0.0331],
[ 0.0061, 0.1823, -0.1050],
[-0.0852, 0.1087, -0.1304]]],
[[[ 0.1367, -0.1686, 0.0111],
[ 0.1147, -0.0931, 0.1092],
[ 0.1872, 0.1117, -0.1616]],
[[ 0.1858, -0.0936, -0.0476],
[-0.0119, -0.1890, -0.1529],
[-0.0828, -0.1012, 0.1378]],
[[ 0.0098, -0.0933, 0.0384],
[ 0.0180, 0.1131, 0.0323],
[ 0.0303, 0.1761, -0.0702]]],
[[[ 0.0155, -0.1876, 0.0168],
[-0.0415, 0.0827, -0.0538],
[-0.1530, -0.1456, 0.1007]],
[[ 0.1888, -0.1168, 0.0222],
[ 0.0502, -0.1053, -0.0102],
[ 0.0270, -0.0658, -0.0467]],
[[-0.0306, -0.0119, 0.1210],
[-0.0173, -0.0074, 0.0379],
[-0.1641, 0.1002, -0.1425]]],
[[[-0.1754, 0.0232, -0.1923],
[-0.0073, 0.0114, -0.1152],
[ 0.0772, -0.1627, -0.0799]],
[[-0.1224, 0.1027, 0.1450],
[-0.1238, 0.0310, 0.0599],
[ 0.0232, 0.1117, -0.1513]],
[[ 0.0757, 0.1777, -0.0022],
[ 0.1185, 0.0331, 0.0219],
[-0.1355, -0.0230, -0.1841]]],
[[[ 0.1517, 0.0229, -0.1478],
[-0.0667, -0.0098, 0.1298],
[-0.1042, -0.0184, -0.1541]],
[[-0.0056, -0.1102, -0.0790],
[-0.1045, 0.0447, 0.1509],
[ 0.0294, 0.0153, 0.1341]],
[[ 0.0491, -0.0482, 0.1387],
[-0.1875, 0.1285, 0.1185],
[ 0.0144, 0.0230, 0.0258]]],
[[[ 0.0062, -0.1263, -0.1183],
[ 0.0234, -0.1225, 0.0616],
[-0.0927, 0.1355, -0.0020]],
[[ 0.0011, 0.1439, -0.1021],
[ 0.1868, 0.0952, -0.0576],
[-0.1754, 0.1162, 0.1530]],
[[ 0.0765, -0.0674, 0.0767],
[-0.0082, -0.1578, 0.1912],
[ 0.0119, -0.1483, 0.0847]]]], requires_grad=True)
偏置项: Parameter containing:
tensor([-0.0581, 0.1005, -0.1702, -0.1158, 0.1891, -0.0035, 0.0777, -0.0847,
0.1701, 0.0380, -0.1917, -0.1452, 0.1276, -0.1446, 0.0636, -0.0750],
requires_grad=True)
这段代码创建了一个二维卷积层 (torch.nn.Conv2d),这是在处理图像或其他二维数据时常用的层。给定的参数表示:
- 输入通道数 (
in_channels):3,这通常对应于RGB图像的三个颜色通道。 - 输出通道数 (
out_channels):16,这表示卷积操作后的特征图数量。 - 卷积核大小 (
kernel_size):3,这意味着卷积核的形状是3x3。
代码接下来将打印卷积层的权重和偏置。
卷积层的权重和偏置的形状及其部分值如下:
-
权重:
- 形状:
16
×
3
×
3
×
3
16 \times 3 \times 3 \times 3
16×3×3×3
- 16 代表输出通道数
- 3 代表输入通道数 (例如 RGB 图像的三个颜色通道)
- 最后的 3x3 代表卷积核的大小
- 形状:
16
×
3
×
3
×
3
16 \times 3 \times 3 \times 3
16×3×3×3
-
偏置:
- 形状: 16 16 16
与全连接层类似,这些权重和偏置是随机初始化的。在训练神经网络时,这些值会根据数据和损失函数进行调整。
3. 池化层
池化层用于减小特征图的空间维度,降低模型的参数数量,并增强模型的平移不变性。最大池化和平均池化是常用的池化方式,它们分别选择局部区域中的最大值和平均值作为输出。
下面是一个创建最大池化层的示例代码:
import torch
import torch.nn as nn
# 定义池化区域大小和步幅
kernel_size = 2
stride = 2
# 创建最大池化层
pool_layer = nn.MaxPool2d(kernel_size, stride)
# 打印最大池化层的参数
print("池化区域大小:", pool_layer.kernel_size)
print("步幅:", pool_layer.stride)
池化区域大小: 2
步幅: 2
这段代码创建了一个最大池化层 (torch.nn.MaxPool2d),它常用于卷积神经网络中减少特征图的空间维度。给定的参数表示:
池化区域大小 (kernel_size):2,这意味着池化操作将在 2x2 的区域上执行。
步幅 (stride):2,这意味着池化窗口每次移动两个像素。
4. 循环神经网络层
循环神经网络(Recurrent Neural Network, RNN)层用于处理序列数据,具有记忆性和上下文感知能力。RNN层通过在时间步之间共享权重,实现对序列的逐步处理,并输出相应的隐藏状态。
下面是一个创建RNN层的示例代码:
import torch
import torch.nn as nn
# 定义输入特征维度、隐藏状态维度和层数
input_size = 10 # 表示每个时间步的输入特征的数量。
hidden_size = 20 # 表示RNN的隐藏状态的大小。
num_layers = 2 # 表示RNN的层数。
# 创建RNN层
rnn_layer = nn.RNN(input_size, hidden_size, num_layers)
# 打印RNN层的参数
print("输入特征维度:", rnn_layer.input_size)
print("隐藏状态维度:", rnn_layer.hidden_size)
print("层数:", rnn_layer.num_layers)
输入特征维度: 10
隐藏状态维度: 20
层数: 2
5. 转置卷积层
转置卷积层,也被称为反卷积层,用于实现上采样操作,将低维特征图转换为高维特征图。转置卷积层通过反向卷积操作将输入特征图映射到更大的输出特征图。
下面是一个创建转置卷积层的示例代码:
这段代码创建了一个转置卷积层(也称为反卷积层,torch.nn.ConvTranspose2d)。
转置卷积层常用于某些卷积神经网络结构,如生成对抗网络(GANs)和某些分割任务,以增加特征图的空间维度。
import torch
import torch.nn as nn
# 定义输入通道数、输出通道数和卷积核大小
in_channels = 3 # 这通常对应于RGB图像的三个颜色通道。
out_channels = 16 # 这表示转置卷积操作后的特征图数量。
kernel_size = 3 # 这意味着卷积核的形状是3x3。
# 创建转置卷积层
transconv_layer = nn.ConvTranspose2d(in_channels, out_channels, kernel_size)
# 打印转置卷积层的权重和偏置项
print("权重:", transconv_layer.weight)
print("偏置项:", transconv_layer.bias)
权重: Parameter containing:
tensor([[[[-4.3310e-02, -2.7487e-02, -1.6882e-02],
[-3.3165e-02, 6.0450e-02, -7.3480e-03],
[-6.3447e-02, 2.8334e-02, -2.4113e-03]],
[[ 3.2450e-02, 7.1121e-03, 7.3090e-02],
[-1.7058e-02, -6.0736e-02, -4.9418e-02],
[-5.3052e-02, 3.5564e-02, 1.2344e-02]],
[[ 1.8053e-03, -5.6241e-04, -3.6630e-02],
[-1.6430e-02, 5.6752e-02, 3.9520e-02],
[ 3.9806e-02, 4.5437e-02, 2.9652e-02]],
[[ 3.5731e-02, -7.4300e-02, -1.0846e-02],
[-1.8894e-02, 1.2247e-02, -3.9685e-02],
[-2.8095e-02, -3.2638e-02, -5.6598e-02]],
[[ 7.3417e-02, -1.0934e-02, -2.7683e-02],
[ 1.6771e-02, -8.1226e-02, -7.0693e-02],
[ 3.3702e-02, 2.7089e-03, -5.1085e-02]],
[[ 6.1530e-02, 4.6181e-02, 1.6004e-02],
[ 5.8891e-02, 2.8858e-02, 6.5992e-02],
[ 7.3270e-02, 4.7769e-03, -2.5520e-02]],
[[ 1.3788e-02, -3.3434e-02, -8.2878e-02],
[ 4.6391e-02, -5.8310e-02, -7.4035e-02],
[-7.7780e-02, 1.4076e-02, -2.5847e-02]],
[[-4.3288e-06, 5.8527e-02, 5.2687e-02],
[-4.6651e-02, 7.3714e-02, 7.7050e-02],
[ 5.0150e-02, 3.7468e-02, 7.0450e-02]],
[[-6.5568e-02, 2.8103e-02, -1.1084e-02],
[ 4.3578e-02, 7.8428e-02, 2.9555e-02],
[ 4.4728e-02, 9.0640e-03, -4.1142e-02]],
[[ 3.0639e-02, 4.1901e-02, -2.9918e-03],
[-1.6603e-02, -4.7129e-03, -7.5677e-02],
[-7.6055e-02, 2.1434e-03, -6.6712e-02]],
[[-3.5669e-02, -3.0165e-02, -2.6293e-02],
[ 7.8248e-02, 3.9015e-02, 7.0101e-02],
[-5.8779e-02, -1.1436e-02, -3.2593e-02]],
[[ 5.6234e-03, -1.8348e-02, -6.5569e-02],
[ 4.8382e-02, 2.6478e-02, 5.7236e-03],
[ 4.0029e-02, 8.3332e-02, 3.7328e-02]],
[[-6.9672e-02, -3.9060e-02, -6.9647e-02],
[ 4.8302e-02, 2.9570e-02, -7.0727e-02],
[-4.2840e-02, -5.2590e-03, -4.8516e-02]],
[[-7.6595e-04, -4.9245e-02, 2.7902e-02],
[-4.8484e-02, -4.0472e-02, 4.0378e-02],
[ 3.2508e-02, 7.3416e-02, 4.8876e-02]],
[[-6.7718e-02, 3.2743e-02, -6.7267e-02],
[ 6.9228e-02, -1.1050e-02, 4.6478e-02],
[ 5.0168e-02, 3.2148e-02, -7.3546e-04]],
[[-5.3274e-02, -6.4141e-02, 7.9356e-03],
[ 4.6557e-02, -6.6722e-02, 1.0326e-02],
[ 4.4060e-02, 5.2210e-02, -8.2268e-02]]],
[[[-7.5545e-02, 4.9937e-02, -3.7531e-02],
[-2.7139e-02, 4.4978e-03, 2.3542e-02],
[-5.3242e-02, 3.9112e-02, -2.4052e-02]],
[[-6.8974e-02, 7.6977e-02, -6.5473e-02],
[-1.6610e-02, 4.8463e-02, 3.5870e-03],
[-5.5097e-02, -8.1178e-03, 2.6279e-02]],
[[ 6.0739e-02, -1.5398e-02, -5.6589e-02],
[ 3.2051e-02, -6.5780e-04, -5.7214e-02],
[ 3.1892e-03, 3.4471e-02, 4.6859e-02]],
[[ 4.2735e-02, -7.9788e-02, -3.8484e-02],
[-7.9190e-02, -4.2851e-02, -7.6756e-02],
[ 3.7714e-02, -4.6119e-02, 2.1634e-02]],
[[-4.0370e-02, -4.8885e-03, -5.4224e-02],
[ 5.2780e-02, 1.6637e-02, -4.5684e-03],
[ 2.9424e-02, -5.8991e-02, 4.4261e-02]],
[[ 5.4214e-02, 8.9623e-03, -4.3044e-02],
[-3.1527e-02, -1.6455e-02, 8.2095e-02],
[ 8.1401e-03, -2.4205e-02, -7.1224e-02]],
[[ 4.5095e-03, -6.4357e-02, 7.6842e-02],
[-1.7547e-02, -6.8445e-02, -4.9015e-02],
[ 9.3632e-03, 6.8596e-02, 6.4922e-03]],
[[ 6.7742e-02, 1.8123e-02, -7.1328e-02],
[ 6.5194e-02, -6.9936e-02, -7.5445e-02],
[ 6.4129e-02, 7.1970e-02, -4.3166e-02]],
[[-2.0678e-02, -3.0602e-02, 2.0784e-02],
[ 3.3409e-02, 6.8187e-02, -2.8919e-02],
[ 2.3555e-02, 1.2323e-02, -5.8928e-02]],
[[ 5.0012e-03, -5.3851e-02, -4.5076e-03],
[-2.8638e-02, 7.9139e-02, -9.5755e-03],
[ 1.4985e-02, -6.0081e-02, -3.3463e-02]],
[[-6.5923e-02, -1.3151e-02, 3.8655e-02],
[ 4.3627e-02, -1.2329e-02, 5.3862e-02],
[-2.6386e-03, 5.0556e-02, 4.5918e-02]],
[[-6.9661e-02, -7.9392e-02, -3.5238e-02],
[ 5.1834e-02, 2.2366e-02, 3.1170e-02],
[-2.1753e-02, -8.6692e-03, -1.8635e-02]],
[[ 9.5781e-03, 2.4513e-02, 8.0391e-02],
[-6.2642e-03, -3.3428e-02, -2.7919e-02],
[ 2.8785e-02, -4.4307e-02, -5.3952e-02]],
[[ 6.8786e-02, -5.3247e-02, 3.4860e-02],
[-1.6302e-02, -6.0792e-02, -5.6724e-02],
[-7.1372e-02, -4.7302e-02, 6.9732e-02]],
[[ 6.3099e-02, -1.0948e-02, -6.2674e-02],
[ 6.7598e-02, 7.0914e-02, 6.3503e-02],
[-1.6821e-02, -4.2196e-02, -8.0121e-02]],
[[ 6.0396e-02, 5.8279e-02, 2.6950e-03],
[ 5.9833e-02, 4.7608e-02, 3.3285e-02],
[ 2.3887e-03, -7.5940e-02, 7.7751e-02]]],
[[[ 8.1936e-02, -1.2425e-02, -3.6663e-02],
[ 4.7825e-02, -1.8580e-02, -2.9987e-02],
[-8.1625e-02, -6.3712e-02, 2.6630e-02]],
[[ 7.3282e-02, 4.0681e-03, -6.5527e-02],
[ 3.4361e-02, -8.1659e-02, -5.1740e-02],
[-8.1514e-02, -7.7867e-02, 7.1171e-02]],
[[-6.3583e-02, -7.5438e-02, 6.5569e-02],
[-4.2764e-03, -6.1021e-02, 8.2998e-02],
[ 5.5737e-02, -4.0857e-02, -8.3524e-03]],
[[-3.6430e-02, 4.0618e-02, 4.8655e-02],
[-5.2642e-03, 7.9419e-03, -8.2692e-03],
[ 3.6112e-02, 2.4779e-02, 3.6723e-02]],
[[-4.0049e-02, -7.8344e-02, 5.9318e-02],
[-4.3901e-02, -5.0245e-02, 3.6794e-02],
[-5.3873e-02, -1.1335e-02, 3.7065e-02]],
[[-6.7667e-02, -7.8498e-02, 1.0819e-02],
[-2.8165e-02, 4.7831e-02, 4.3574e-02],
[ 4.7185e-02, 3.0248e-02, -3.8408e-02]],
[[-1.9840e-02, 2.9312e-02, -7.0882e-02],
[ 7.4346e-02, 6.4234e-02, 6.9513e-02],
[ 5.8193e-02, -9.0852e-03, 6.5697e-02]],
[[-4.0098e-02, 6.8910e-02, -6.2048e-02],
[-7.8067e-02, 6.1558e-02, -3.9109e-03],
[-2.6566e-02, -8.0330e-02, -5.8488e-02]],
[[ 5.3936e-02, 7.9680e-02, -1.6630e-02],
[ 5.9345e-02, 3.8390e-02, 3.8418e-02],
[ 8.2005e-02, 2.9200e-02, -3.7427e-02]],
[[ 4.9153e-03, 9.1106e-03, -4.0126e-02],
[-2.8253e-02, -1.2580e-02, 4.3137e-02],
[ 4.7532e-02, -4.1056e-02, 7.1148e-03]],
[[ 7.2846e-02, 2.1844e-02, -7.5763e-02],
[-7.6639e-02, 2.6490e-02, 3.4289e-02],
[-3.3318e-02, 7.8411e-02, -5.5555e-02]],
[[ 5.4056e-02, 7.9220e-02, -5.5332e-02],
[-6.1049e-02, 1.2875e-02, -6.6220e-02],
[-7.3244e-02, -8.0434e-02, 2.9077e-02]],
[[-3.6276e-03, 2.7413e-02, 5.1244e-02],
[-1.2177e-02, -1.0273e-02, -5.8908e-02],
[-3.6779e-02, -6.7766e-02, -2.7649e-02]],
[[-6.6113e-02, 4.5632e-02, -8.3198e-02],
[-6.7047e-02, -1.2116e-02, -4.8435e-02],
[ 7.0850e-02, 5.2572e-02, -6.4721e-02]],
[[ 6.6159e-02, -2.6158e-02, 6.9201e-02],
[-5.9506e-02, -5.2811e-02, 3.4745e-02],
[ 6.7963e-02, 5.6720e-02, -8.1097e-02]],
[[-6.8577e-02, -1.9387e-02, -1.0894e-02],
[ 6.4100e-02, 5.3918e-02, 5.3898e-02],
[-6.3463e-02, -4.1229e-02, -8.2298e-02]]]], requires_grad=True)
偏置项: Parameter containing:
tensor([-0.0303, -0.0621, -0.0821, -0.0447, -0.0314, 0.0016, -0.0212, 0.0384,
0.0464, 0.0432, -0.0106, 0.0067, -0.0800, 0.0459, 0.0688, 0.0019],
requires_grad=True)
6. 归一化层
归一化层用于调整神经网络的激活值分布,提升模型的收敛速度和泛化能力。常用的归一化层包括批归一化(Batch Normalization)和层归一化(Layer Normalization)。
下面是一个创建批归一化层的示例代码:
import torch
import torch.nn as nn
# 定义特征维度
num_features = 16 # 表示输入特征图的数量。
# 创建批归一化层
bn_layer = nn.BatchNorm2d(num_features)
# 打印批归一化层的参数
print("特征维度:", bn_layer.num_features)
print("均值:", bn_layer.running_mean) # 所有值都初始化为 0。这代表对于每个特征图,其均值初始化为 0。
print("方差:", bn_layer.running_var) # 所有值都初始化为 1。这代表对于每个特征图,其方差初始化为 1。
特征维度: 16
均值: tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
方差: tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
7. 激活函数层
激活函数层用于引入非线性变换,增加神经网络的表达能力。常用的激活函数包括ReLU、Sigmoid和Tanh等。
下面是一个使用ReLU激活函数的示例代码:
这段代码首先创建了一个 ReLU 激活函数层,然后使用这个激活函数来转换一个随机生成的输入张量。
ReLU (Rectified Linear Unit) 是深度学习中最常用的激活函数之一。它的作用是将所有负值设为 0,而正值保持不变。
import torch
import torch.nn as nn
# 创建激活函数层(ReLU)
activation_layer = nn.ReLU()
# 定义输入张量
input_tensor = torch.randn(10)
# 对输入张量进行激活函数变换
output_tensor = activation_layer(input_tensor)
# 打印输出张量
print("输出张量:", output_tensor)
输出张量: tensor([0.0000, 0.6719, 0.7634, 0.0000, 0.0000, 0.1871, 0.4174, 1.9824, 1.1420,
1.7112])
三、数据加载与预处理
在深度学习任务中,数据的加载和预处理是非常重要的步骤。PyTorch提供了强大的数据加载和预处理工具,使得我们能够高效地处理各种类型的数据。这里将介绍PyTorch中的数据加载和预处理方法,并提供使用示例。
1. 数据加载
PyTorch中的数据加载主要通过torch.utils.data模块实现。该模块提供了Dataset和DataLoader两个核心类,分别用于定义数据集和数据加载器。
🚩Dataset
Dataset类是一个抽象类,用于表示数据集。我们可以继承该类并实现自定义的数据集。在自定义数据集中,我们需要实现两个方法:__len__和__getitem__。__len__方法返回数据集的样本数量,__getitem__方法根据索引返回单个样本。
以下是一个自定义数据集的示例:
这段代码定义了一个自定义的数据集类 MyDataset,它继承自 torch.utils.data.Dataset。自定义的数据集通常需要实现三个主要方法:
__init__(self, ...): 初始化数据集,可以接受任何必要的参数。__len__(self): 返回数据集的大小。__getitem__(self, index): 根据索引获取样本。
在你的代码中:
__init__方法接受一个数据列表 (data_list) 并将其存储为成员变量。__len__方法返回data_list的长度。__getitem__方法返回data_list中指定索引的样本。
这种数据集定义方式非常简单,适用于你已经有一个完整的数据列表的情况。如果你的数据在硬盘上,例如图像文件,那么你可能还需要在 __getitem__ 方法中添加加载和预处理数据的代码。
import torch
from torch.utils import data
from torch.utils.data import Dataset
class MyDataset(data.Dataset):
def __init__(self, data_list):
# 初始化数据集
self.data_list = data_list
def __len__(self):
# 返回数据集大小
return len(self.data_list)
def __getitem__(self, index):
# 根据索引获取样本
sample = self.data_list[index]
return sample
在上述示例中,MyDataset类接受一个数据列表作为输入,并实现了__len__和__getitem__方法。
🚩DataLoader
torch.utils.data.DataLoader是PyTorch中一个重要的类,用于高效加载数据集。它可以处理数据的批次化、打乱顺序、多线程数据加载等功能。以下是一个简单的示例:
import torch.utils.data as data
my_dataset = MyDataset([1, 2, 3, 4, 5])
my_dataloader = data.DataLoader(my_dataset,
batch_size=4, # 每个批次的大小。在这里,它被设置为4。
shuffle=True) # 是否在每个epoch开始时混洗数据。在这里,它被设置为True,这意味着数据将被混洗。
# 请注意,由于我们设置了 shuffle=True,因此每次运行此代码时,批次数据的顺序可能会有所不同。
# 同时,由于数据集中只有5个元素,且批次大小为4,所以第一个批次包含4个元素,第二个批次只包含1个元素。
for batch in my_dataloader:
print(batch)
tensor([3, 5, 1, 4])
tensor([2])
在这个示例中,我们首先创建了一个MyDataset实例my_dataset,它包含了一个整数列表。然后,我们使用DataLoader类创建了一个数据加载器my_dataloader,它将my_dataset作为输入,并将数据分成大小为4的批次,并对数据进行随机化。最后,遍历my_dataloader,并打印出每个批次的数据。
总结一下,torch.utils.data.Dataset用于构建数据集,torch.utils.data.DataLoader用于加载数据集,并对数据进行批量处理和随机化。下面是一个完整的示例,展示了如何使用这两个类来加载和处理数据:
import torch.utils.data as data
class MyDataset(data.Dataset):
def __init__(self, data_list):
# 初始化数据集
self.data_list = data_list
def __len__(self):
# 返回数据集大小
return len(self.data_list)
def __getitem__(self, index):
# 根据索引获取样本
sample = self.data_list[index]
return sample
my_dataset = MyDataset([1, 2, 3, 4, 5])
my_dataloader = data.DataLoader(my_dataset,
batch_size=4,
shuffle=True)
for batch in my_dataloader:
print(batch)
tensor([3, 1, 4, 5])
tensor([2])
除了上述介绍的基本用法,torch.utils.data模块还有许多其他的功能和选项。下面介绍一些常用的选项和功能。
2. 数据预处理
数据预处理是在将数据输入模型之前对数据进行的一系列操作,以提高模型的性能和准确性。PyTorch提供了多种数据预处理方法,包括常见的数据变换、标准化、图像增强等。以下是一些常见的数据预处理方法:
🚩Tensor转换
将数据转换为torch.Tensor类型是数据预处理的第一步。torch.Tensor是PyTorch中表示张量的主要数据类型。
import torch
data = [1,2,3,4,5]
tensor = torch.tensor(data)
tensor
tensor([1, 2, 3, 4, 5])
🚩数据变换
数据变换是对数据进行形状调整或维度变换的操作。PyTorch提供了一系列的数据变换方法,如torchvision.transforms模块中的Resize、ToTensor等。
from torchvision import transforms
transform = transforms.Compose([
transforms.Resize((224, 224)), # 将图像调整为大小为 224×224
transforms.ToTensor() # 将图像转换为PyTorch张量,并将其值范围从 [0, 255] 调整为 [0, 1]。
])
# 对数据进行变换
transformed_data = transform(data) # data 变量还没有被定义或指定。
🚩数据标准化
数据标准化是对数据进行平均值和标准差的缩放,以使得数据具有零均值和单位方差。这通常用于提高模型的收敛性和稳定性。
在这段代码中,你使用 torchvision.transforms 创建了一个标准化变换 normalize:
- 使用
transforms.Normalize(...)对图像进行标准化。标准化是使用预计算的均值和标准差来调整图像通道的一种方法。这里给出的均值和标准差是对ImageNet数据集的预计算结果,经常用于预训练模型。
import torchvision.transforms as transforms
normalize = transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
# 对图像进行标准化
normalized_image = normalize(image) # 我们需要一个输入图像来应用这个变换。但和之前一样,image 变量尚未被定义或指定。
🚩图像增强
图像增强是对图像进行变换或添加噪声,以增加训练数据的多样性和鲁棒性。PyTorch提供了torchvision.transforms模块中的多种图像增强方法,如随机裁剪、翻转、旋转等。
import torchvision.transforms as transforms
transform = transforms.Compose([
transforms.RandomCrop(224), # 对图像进行随机裁剪,得到 224×224 的图像。
transforms.RandomHorizontalFlip(), # 随机地对图像进行水平翻转。
transforms.RandomRotation(30) # 随机地在 [−30°,30°] 范围内旋转图像。
])
# 对图像进行增强
transformed_image = transform(image) # 尝试使用此变换序列 transform 对 image 进行变换。我们需要一个输入图像来应用这个变换。但和之前一样,image 变量尚未被定义或指定。
本节介绍了PyTorch中的数据加载和预处理方法。通过自定义数据集和数据加载器,我们可以高效地加载和处理数据。同时,PyTorch提供了多种数据预处理方法,如数据变换、标准化和图像增强,以提高模型的性能和准确性。
四、模型训练与验证
1. 模型训练
PyTorch中的模型训练主要涉及以下几个步骤:
- 准备数据:首先,我们需要准备好训练数据和对应的标签。可以使用
torch.utils.data模块中的Dataset和DataLoader类来加载和批量处理数据。 - 定义模型:接下来,我们需要定义模型的结构。可以使用
torch.nn模块中的各种层和模型来构建自己的神经网络模型。 - 定义损失函数:为了训练模型,我们需要定义损失函数来度量模型预测结果与真实标签之间的差异。可以使用
torch.nn模块中的各种损失函数,如均方误差(MSE)、交叉熵损失等。 - 定义优化器:为了更新模型的参数,我们需要选择一个优化器来优化模型的损失函数。可以使用
torch.optim模块中的各种优化器,如随机梯度下降(SGD)、Adam等。 - 训练模型:在每个训练迭代中,我们需要执行以下步骤:
- 前向传播:将输入数据通过模型,得到模型的输出结果。
- 计算损失:将模型的输出结果与真实标签计算损失函数的值。
- 反向传播:根据损失函数的梯度,计算模型参数的梯度。
- 参数更新:使用优化器根据梯度信息更新模型的参数。
以下是一个简单的模型训练示例:
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
# 准备数据
train_dataset = MyDataset(train_data) # 用之前定义的 MyDataset 类创建了一个数据集实例 train_dataset
# 通过 DataLoader 创建了一个数据加载器 train_dataloader。
train_dataloader = DataLoader(train_dataset,
batch_size=64,
shuffle=True)
# 定义模型
model = MyModel() # 使用自定义的 MyModel 类创建了一个模型实例 model。
# 定义损失函数
loss_fn = nn.CrossEntropyLoss() # 使用了交叉熵损失,这是多分类问题的常见选择。
# 定义优化器
optimizer = optim.SGD(model.parameters(), lr=0.01) # 选择了随机梯度下降 (SGD) 作为优化算法。
# 模型训练
for epoch in range(num_epochs): # 进行了多个epoch的训练,每个epoch都遍历了整个训练数据集。
for batch in train_dataloader: # 对于每个批次,执行了以下操作:前向传播、计算损失、反向传播、参数更新
inputs, labels = batch
# 前向传播
outputs = model(inputs)
# 计算损失
loss = loss_fn(outputs, labels)
# 反向传播
optimizer.zero_grad()
loss.backward()
# 参数更新
optimizer.step()
在上述示例中,我们使用自定义的数据集和数据加载器准备训练数据,定义了模型、损失函数和优化器,并在每个训练迭代中执行了前向传播、计算损失、反向传播和参数更新的步骤。
然而,这段代码中有一些未定义的变量或类,如 train_data, MyModel, 和 num_epochs。你需要确保这些变量或类在执行上述代码之前已经定义或导入。
此外,如果 MyDataset 返回的批次数据是单个张量(而不是输入-标签对),那么 inputs, labels = batch 这行代码将会引发错误。
如果你想要运行这段代码,请确保提供所有必要的定义,并确保 MyDataset 返回正确的数据格式。
2. 模型验证
在模型训练之后,我们需要对模型进行验证以评估其性能和准确性。模型验证的步骤与模型训练类似,但不需要进行参数更新。
以下是一个简单的模型验证框架:
# 准备验证数据
val_dataset = MyDataset(val_data) # 使用之前定义的 MyDataset 类创建了一个验证数据集实例 val_dataset
val_dataloader = DataLoader(val_dataset, batch_size=64) # 通过 DataLoader 创建了一个数据加载器 val_dataloader。
# 模型验证
model.eval() # 设置模型为评估模式 ,这是一个重要步骤,因为某些层(如Dropout和BatchNorm)在训练和评估时具有不同的行为。
with torch.no_grad(): # 禁止梯度计算, 这是因为在验证阶段,我们不需要反向传播或参数更新,所以可以禁用梯度来节省计算资源。
for batch in val_dataloader: # # 对于 val_dataloader 中的每个批次,执行前向传播。
inputs, labels = batch
# 前向传播
outputs = model(inputs)
# 在这里可以对模型输出进行后处理,如计算准确率、绘制预测结果等
在上述示例中,我们使用自定义的验证数据集和数据加载器准备验证数据,并使用model.eval()将模型设置为评估模式。然后,在验证数据上进行前向传播,并根据需要对模型输出进行后处理。
但要使其完整工作,你需要确保所有必要的定义都在这之前进行,例如 val_data, MyDataset, 和 model。此外,根据 MyDataset 的实现,你可能还需要对数据加载和处理部分进行调整。
介绍了PyTorch中的模型训练和验证方法。通过准备数据、定义模型、损失函数和优化器,以及执行训练和验证循环,我们可以高效地训练和评估深度学习模型。
闯关练习
👉练习1: 请使用 .DataLoader 加载列表 [12,1,2,3,4,5] 到my_dataloader,batch_size 设置为3,不打乱数据,输出my_dataloader,并将第一行输出放到answer1中
import torch
from torch.utils.data import DataLoader, TensorDataset
# 数据
data_list = [12, 1, 2, 3, 4, 5]
# 转换为TensorDataset
dataset = TensorDataset(torch.tensor(data_list))
# 使用 DataLoader 加载数据
batch_size = 3
my_dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=False)
# 输出第一行
first_batch = next(iter(my_dataloader))
answer1 = first_batch[0].tolist()
answer1
[12, 1, 2]
👉练习2: 请使用 .DataLoader 加载列表 [12,1,2,3,4,5] 到my_dataloader,batch_size 设置为4,不打乱数据,输出my_dataloader,并将第最后一行输出放到answer2中
# 使用 DataLoader 加载数据,这次 batch_size 为 4
batch_size_2 = 4
my_dataloader_2 = DataLoader(dataset, batch_size=batch_size_2, shuffle=False)
# 输出最后一行
last_batch = None
for batch in my_dataloader_2:
last_batch = batch
answer2 = last_batch[0].tolist()
answer2
[4, 5]