文章目录
- 梯度下降法
- 梯度下降法原理(通俗版)
- 梯度下降法公式
- 学习率的设置
- **如何选择学习率?**
- 全局最优解
- 梯度下降法流程
- 损失函数的导函数
- 三种梯度下降法
- **梯度下降法核心步骤回顾**
- **优缺点详解**
- **1. 全量梯度下降 (Batch Gradient Descent, BGD)**
- **2. 随机梯度下降 (Stochastic Gradient Descent, SGD)**
- **3. 小批量梯度下降 (Mini-Batch Gradient Descent, MBGD)**
- **三种梯度下降的区别与对比**
- 如何选择?
- 梯度下降法的问题与挑战
梯度下降法
- 梯度下降法(Gradient Descent):是一个非常通用的优化算法帮助机器学习求解最优解。所有优化算法的目的都是期待以最快的速度求解模型参数θ,梯度下降就是一种经典常用的优化算法。
- 使用梯度下降法的原因:
- 如果机器学习的损失函数是非凸函数,使用解析解公式求解θ,设置梯度为0会得到很多极值,甚至可能是极大值。
- 解析解计算成本高 :当特征维度N较大时,解析解需要计算矩阵的逆(复杂度O(N³)),计算时间呈指数级增长。例如,特征数量从4增加到16,计算时间会从1秒暴增到64秒。
- 更适合高维和大规模数据:梯度下降法通过迭代逼近最优解,避免了直接求逆的计算瓶颈,尤其适合特征维度高或数据量大的场景(如深度学习)。
- 动态优化的优势:解析解需要一次性求解,而梯度下降可以逐步优化,灵活适应在线学习或超大规模数据的分批训练。

梯度下降法原理(通俗版)
- 初始化:随机猜一个起点:就像猜工资时先随便说个数,计算机一开始也会随机给参数θ(比如W₁, W₂…Wₙ)赋一组初始值。
- 计算误差(Loss):用当前的θ预测结果(ŷ),并计算预测值ŷ和真实值y的差距(比如用均方误差MSE)。 目标:让这个误差越小越好。
- 调整参数:根据反馈改进:如果误差变小了:说明调整方向正确,继续按这个方向微调θ;如果误差变大了:说明调反了,换个方向调整(比如增大改减小,或反之)。
- 重复直到最优:像“道士下山”一样,一步步试探,最终找到误差最低的θ(山谷最低点)。
- 核心思想**“猜-反馈-改进”循环**,通过不断试错逼近最优解,而不是直接计算复杂公式。
类比简化
- 猜工资游戏: 朋友说“高了/低了”,你逐步逼近正确答案。
- 梯度下降:计算机用“误差”反馈(如MSE)指导参数调整方向,直到最优。
梯度下降法公式
- 参数更新公式:
W j ( t + 1 ) = W j ( t ) − η ⋅ gradient j W_j^{(t+1)} = W_j^{(t)} - \eta \cdot \text{gradient}_j Wj(t+1)=Wj(t)−η⋅gradientj - 符号说明:
- W j ( t ) W_j^{(t)} Wj(t):第 t t t轮迭代时的参数 W j W_j Wj( θ \theta θ 中的一个分量)。
- η \eta η(或 α \alpha α):学习率(learning rate),控制每次调整的步长(类似“下山时的步幅”)。
- gradient j \text{gradient}_j gradientj:损失函数对 W j W_j Wj的梯度(即当前方向上的“最陡下降方向”)。
核心作用:
- 梯度(gradient) 告诉参数“往哪个方向调整能最快降低误差”。
- 学习率(η) 决定调整的幅度:
- η太大 → 可能“跨过”最优解(震荡甚至发散)。
- η太小 → 收敛慢(下山速度太慢)。

关键点:
- 梯度决定方向(往哪走),学习率决定步幅(走多远)。
- 所有参数 W j W_j Wj同时按各自梯度调整,直到收敛。
- 公式的直观意义:“沿着梯度方向,迈一小步,反复走,直到最低点。”
新参数 = 旧参数 − 步长 × 最陡方向 \text{新参数} = \text{旧参数} - \text{步长} \times \text{最陡方向} 新参数=旧参数−步长×最陡方向
学习率的设置
- 权重更新公式:
W
j
t
+
1
=
W
j
t
−
η
⋅
gradient
j
W_{j}^{t+1} = W_{j}^{t} - \eta \cdot \text{gradient}_j
Wjt+1=Wjt−η⋅gradientj
- W j t W_{j}^{t} Wjt:当前权重
- η \eta η(eta):学习率(控制每次调整的幅度)
-
gradient
j
\text{gradient}_j
gradientj:损失函数对权重的梯度
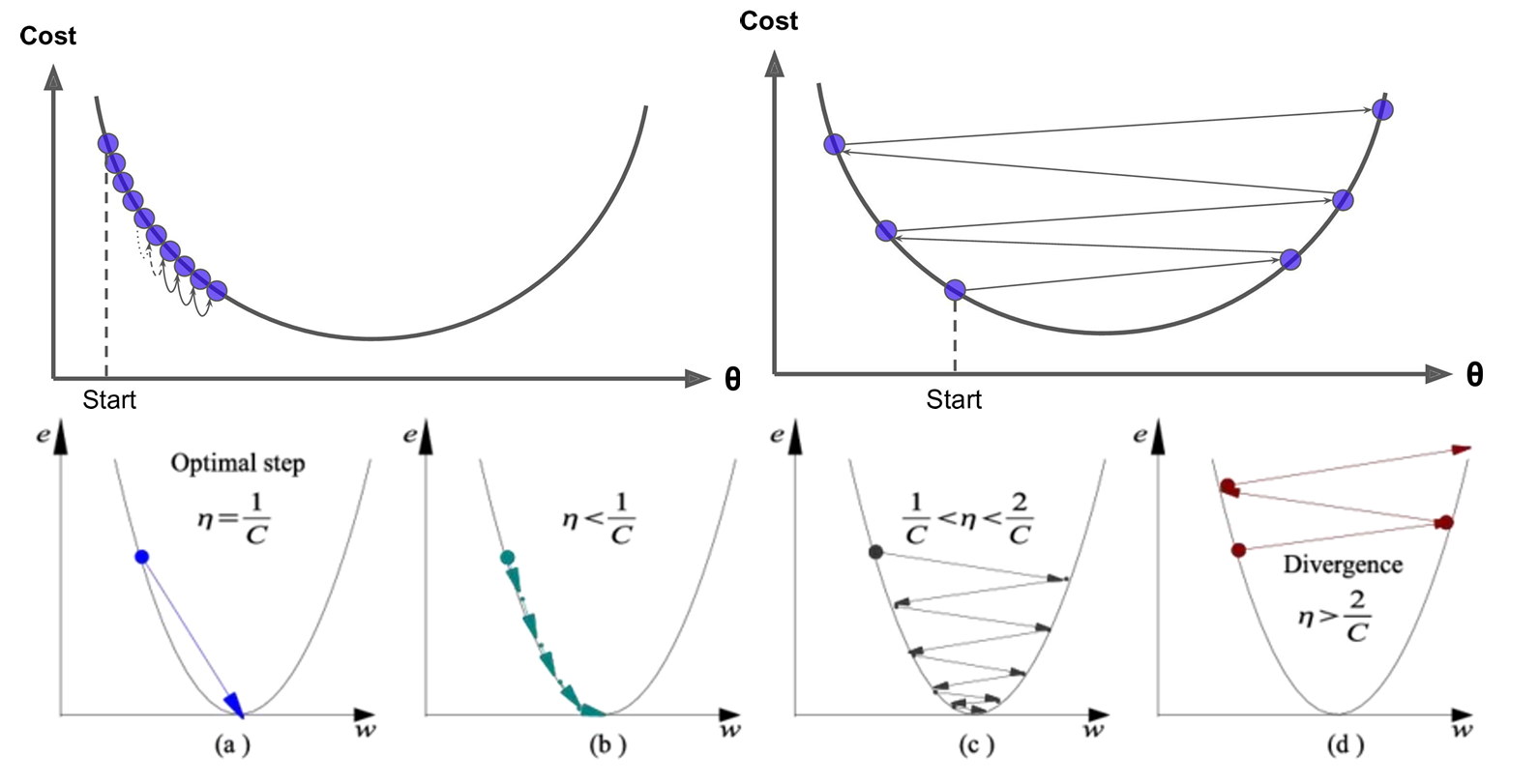
- 学习率的影响
- 学习率太大(如 η=1.0):调整幅度过大,容易“跨过”最优解,导致震荡甚至无法收敛。类似“步子太大,容易走过头,来回摇摆”。
- 学习率太小(如 η=0.0001):每次调整幅度过小,收敛速度极慢,训练时间大幅增加。类似“小碎步前进,要走很久才能到达目标”。
如何选择学习率?
✅ 常用初始值:0.1、0.01、0.001、0.0001(根据问题调整)
✅ 动态调整策略:
- 学习率衰减:随着训练进行,逐步减小 η(越接近最优解,步伐越小)。
- 自适应优化算法:如 Adam、RMSprop 等,自动调整学习率。

全局最优解

- 如果损失函数是非凸函数,梯度下降法是有可能落到局部最小值的,所以其实步长不能设置的太小太稳健,那样就很容易落入局部最优解,虽说局部最小值也没大问题,因为模型只要是堪用的就好嘛,但是我们肯定还是尽量要奔着全局最优解去。
梯度下降法流程

- 梯度下降法就像一个人蒙着眼睛下山的过程,通过不断试探找到最低点。
- 以下是具体步骤:
- 随机初始化:先随便猜一组参数值(θ或W),就像随机站在山上的某个点。
- 实现方法:
np.random.rand()或np.random.randn()
- 实现方法:
- 计算梯度:计算当前位置的"坡度"(梯度)。梯度是损失函数在该点的斜率,指向最陡上升方向。
- 关键点:梯度指向上升方向,所以我们要往反方向走才能下降。
- 参数更新:
- 如果梯度(g)为负 → 需要增大θ
- 如果梯度(g)为正 → 需要减小θ
- 更新公式: θ n e w = θ o l d − η × g r a d i e n t θ_{new} = θ_{old} - η×gradient θnew=θold−η×gradient (η是学习率,控制步长)
- 判断收敛:
- 不能简单判断梯度=0(可能是局部最低或最高点)
- 更好的方法是观察损失值的变化:当损失值基本不再下降时停止
- 实际做法:设置阈值,当损失变化小于阈值时停止
- 关键问题
- 如何随机初始化?:使用随机函数生成初始参数值
- 如何计算梯度?:需要求损失函数对各个参数的偏导数(这是后续要详细讲解的部分)
- 如何调整参数?:按照公式:新参数 = 旧参数 - 学习率×梯度
- 如何判断收敛?:监测损失值的变化幅度,而不是梯度本身
损失函数的导函数
- 推导损失函数的导函数

- J ( θ ) J(θ) J(θ)是损失函数
- θ j θ_j θj是某个特征维度 X j X_j Xj对应的权值系数
- 损失函数是MSE,MSE中x、y是已知的,θ是未知的,而θ不是一个变量而是一堆变量。所以我们只能对含有一推变量的函数MSE中的一个变量求导,即偏导,下面就是对
θ
j
θ_j
θj求偏
导。


三种梯度下降法
梯度下降法核心步骤回顾
- 初始化参数:随机生成初始参数(θ/W)。
- 计算梯度:求损失函数对参数的偏导(梯度),确定下降方向。
- 更新参数:沿梯度反方向调整参数(学习率η控制步长)。
- 判断收敛:通过损失变化或梯度接近零终止迭代。
优缺点详解
1. 全量梯度下降 (Batch Gradient Descent, BGD)

- 公式:
θ j t + 1 = θ j t − η ⋅ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_{j}^{t+1} = \theta_{j}^{t} - \eta \cdot \frac{1}{m} \sum_{i=1}^{m} \left( h_{\theta}(x^{(i)}) - y^{(i)} \right) x_{j}^{(i)} θjt+1=θjt−η⋅m1i=1∑m(hθ(x(i))−y(i))xj(i)
说明: - θ j t \theta_{j}^{t} θjt: 第 t t t 次迭代的参数 θ j \theta_j θj(第 j j j 维)。
- η \eta η: 学习率(步长)。
- m m m: 训练集总样本数。
- h θ ( x ( i ) ) h_{\theta}(x^{(i)}) hθ(x(i)): 模型对样本 x ( i ) x^{(i)} x(i)的预测值。
- 特点:每次迭代使用全部样本计算梯度,更新稳定但计算成本高。
- 优点:
- 梯度方向准确,收敛稳定(数学上保证凸函数的全局最优)。
- 易于并行化(因梯度计算依赖全数据集)。
- 缺点:
- 计算成本高(每次迭代需遍历全部数据)。
- 内存占用大,无法处理超出内存的数据集。
- 对非凸函数可能陷入局部最优。
2. 随机梯度下降 (Stochastic Gradient Descent, SGD)

公式:
θ
j
t
+
1
=
θ
j
t
−
η
⋅
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\theta_{j}^{t+1} = \theta_{j}^{t} - \eta \cdot \left( h_{\theta}(x^{(i)}) - y^{(i)} \right) x_{j}^{(i)}
θjt+1=θjt−η⋅(hθ(x(i))−y(i))xj(i)
说明:
- i i i: 随机选取的单个样本索引( i ∼ Uniform ( 1 , m ) i \sim \text{Uniform}(1, m) i∼Uniform(1,m))。
- 特点:每次迭代仅用一个样本更新参数,计算快但噪声大。
- 优点:
- 计算速度快,适合大规模或流式数据。
- 随机性可能逃离局部最优(非凸优化中表现更好)。
- 缺点:
- 梯度估计噪声大,收敛不稳定(需精细调节学习率)。
- 难以并行化(因更新依赖单个样本)。
3. 小批量梯度下降 (Mini-Batch Gradient Descent, MBGD)

公式:
θ
j
t
+
1
=
θ
j
t
−
η
⋅
1
b
∑
i
=
k
k
+
b
−
1
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\theta_{j}^{t+1} = \theta_{j}^{t} - \eta \cdot \frac{1}{b} \sum_{i=k}^{k+b-1} \left( h_{\theta}(x^{(i)}) - y^{(i)} \right) x_{j}^{(i)}
θjt+1=θjt−η⋅b1i=k∑k+b−1(hθ(x(i))−y(i))xj(i)
说明:
- b b b: 小批量大小(通常 b ∈ [ 32 , 256 ] b \in [32, 256] b∈[32,256])。
- k k k: 当前批次的起始样本索引。
- 特点:折中方案,平衡计算效率和稳定性。
- 优点:
- 平衡BGD的稳定性和SGD的速度(主流深度学习选择)。
- 可利用GPU并行计算小批量数据。
- 缺点:
- 需手动调节批量大小(k)和学习率。
- 仍存在一定噪声(但比SGD小)。
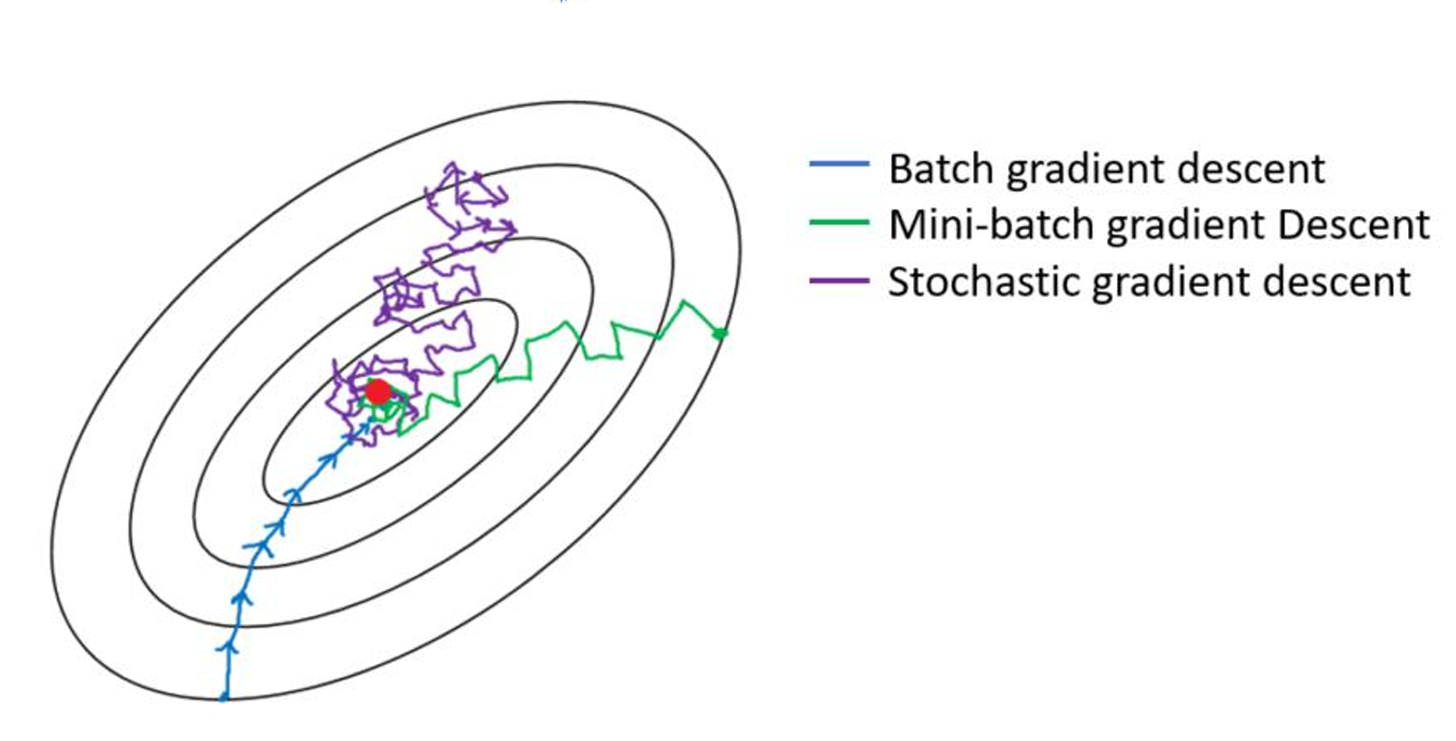
收敛路径:
BGD → 平滑但慢
SGD → 快速但震荡
MBGD → 折中方案
三种梯度下降的区别与对比
| 类型 | 全量(批量)梯度下降 (BGD) | 随机梯度下降 (SGD) | 小批量梯度下降 (MBGD) |
|---|---|---|---|
| 每次迭代的样本量 | 全部样本(N) | 单个样本(1) | 小批量样本(k,通常32-256) |
| 梯度计算方式 | 真实梯度(全局平均) | 噪声梯度(单个样本的估计) | 近似梯度(局部平均) |
| 参数更新频率 | 每轮迭代1次更新 | 每样本1次更新 | 每k个样本1次更新 |
| 收敛性 | 稳定,但可能陷入局部最优 | 不稳定,震荡大 | 平衡稳定性和随机性 |
| 计算效率 | 慢(尤其大数据集) | 快(适合在线学习) | 适中(GPU并行优化友好) |
| 内存需求 | 高(需加载全部数据) | 低 | 中 |
| 适用场景 | 凸函数、小数据集 | 非凸优化、大规模数据 | 深度学习等大多数场景 |
如何选择?
- 数据量小 → BGD(确保精度)。
- 数据量大/在线学习 → SGD(牺牲稳定性换速度)。
- 深度学习/默认推荐 → MBGD(批量大小常选32/64/128)。







![42.[前端开发-JavaScript高级]Day07-手写apply-call-bind-块级作用域](https://i-blog.csdnimg.cn/direct/18a5845b1b3344299130251e35dd2bae.png)