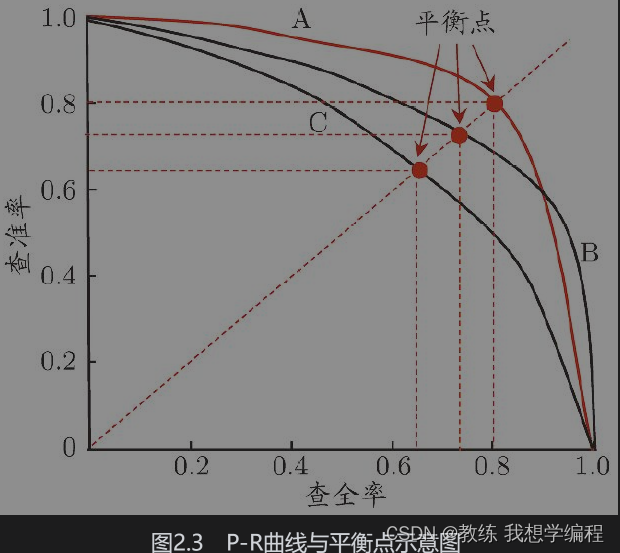
查准率和查全率定义
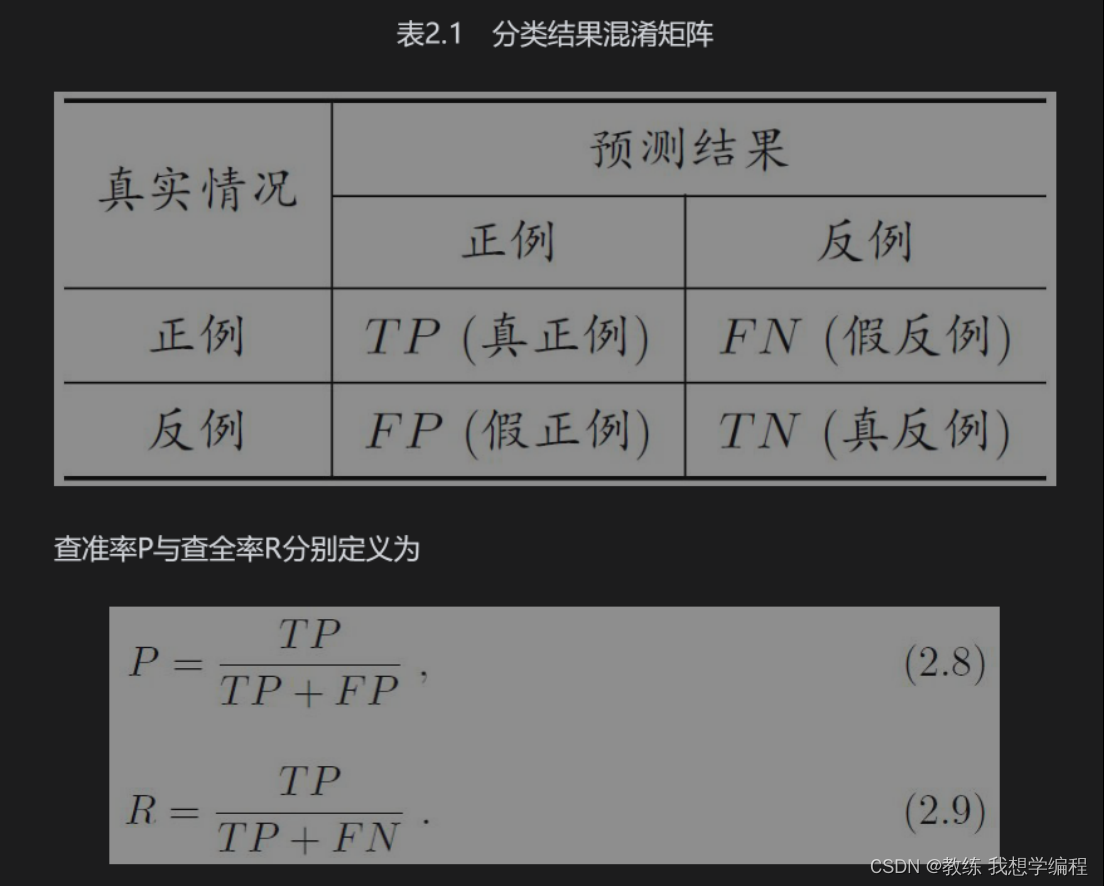
查准率与查全率真的必然负相关吗?
先说结论,两者并非绝对负相关,只是在统计学上表现出大概率的负相关性,而数学证明上无法严格证明两个的负相关性。
枚举来证明两者并非必然负相关
一组数据:A1、B1、C1、D0、E0、F0,其中1代表正例,0代表反例。
第一次分类预测:预测为正例的样本为:A1、B1、D0,预测为反例的样本为:C1、E0、F0,此时TP=2,FP=1 ,FN=1,TN=2,P=2/3,R=2/3。
第二次分类预测,提高P值:预测为正例的样本为:A1、B1、C1、D0,预测为反例的样本为:E0、F0,此时TP=3,FP=1 ,FN=0,TN=2,P=3/4,R=1。
从以上枚举可以发现,提高P,R也可以提高,因此证明了并非查准率与查全率真的必然负相关。
逻辑推理证明两者负相关的概率比较大
对于R值,分母TP+FN=样本真实的正例数量,必然保持不变。因此要提高R值,则只能提高TP,在此条件下,再来看P值,分子提高,但是逻辑上来说,如果要提高分子,也就是预测正例正确的数量,那么在其他条件一致的情况下(比如预测的机制不变),只有尽可能多的预测,比如之前预测10个正例,正确5个,要使得TP增加,在不改变预测机制的情况下就只能预测30个正例,从概率上来说可能预测正确的数量会高于5个,但是因为预测正例的数量增加了,概率上来说FP也增加了,因此综合起来,TP增加的速度可能小于TP+FP增加的速度,因此P值实际上可能是降低的,因为分子增加的速度小于分母增加的速度。所以真实的PR曲线是非光滑的,也并非是一直是复斜率的。