目录
一、首次适应算法
1、算法思想:
2、如何实现:
3、两种常用的数据结构:
(1)空闲分区表、空闲分区链
4、例子
二、最佳适应算法
1、算法思想:
2、如何实现:
3、例子:
三、最坏适应算法
1、算法思想:
2、如何实现:
3、例子
4、缺点
四、临近适应算法
算法思想:
如何实现:
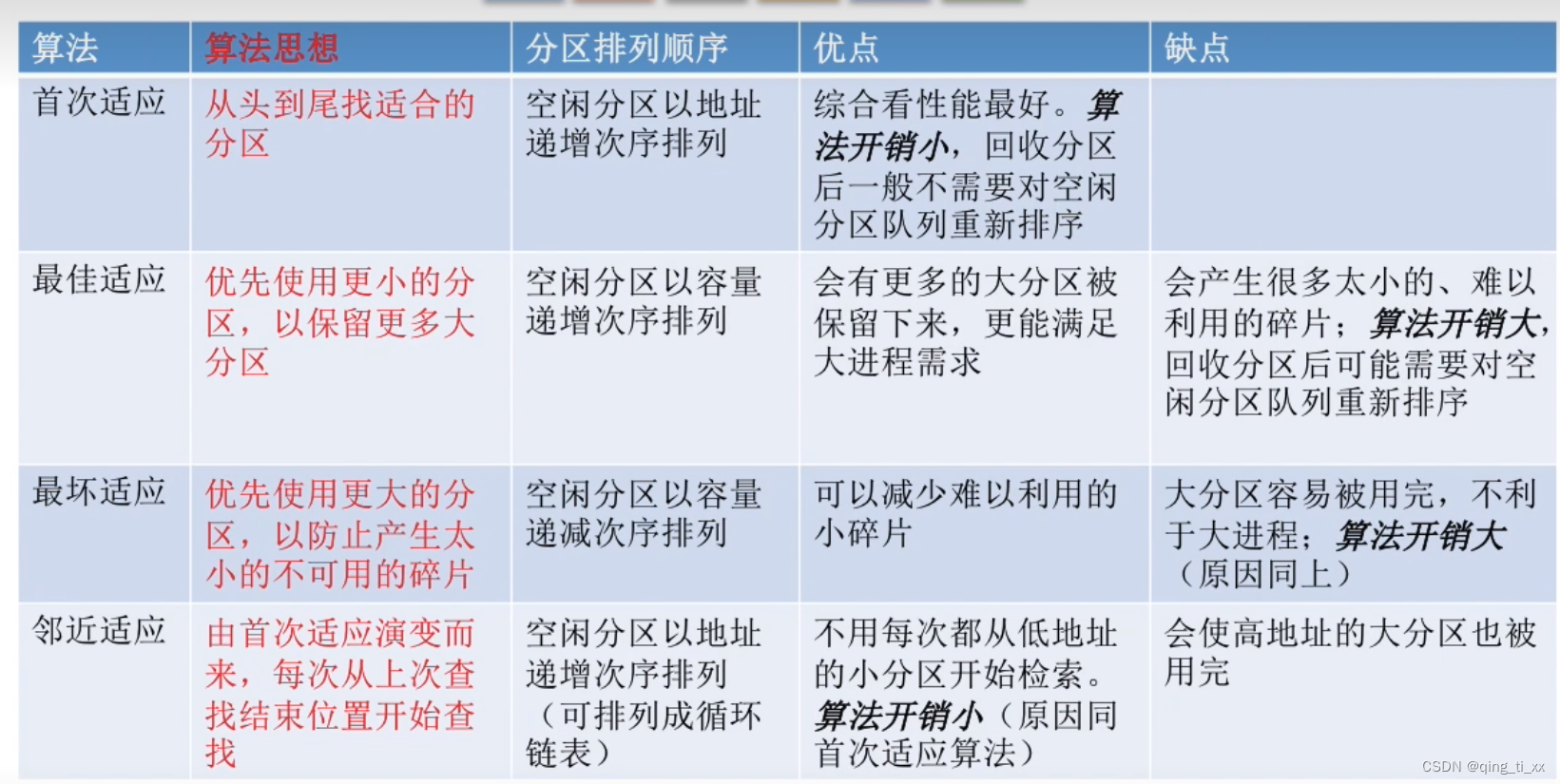
五、总结
一、首次适应算法
1、算法思想:
每次都从低地址开始查找,找到第一个能满足大小的空闲分区。
2、如何实现:
空闲分区以地址递增的次序排列。每次分配内存时顺序查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
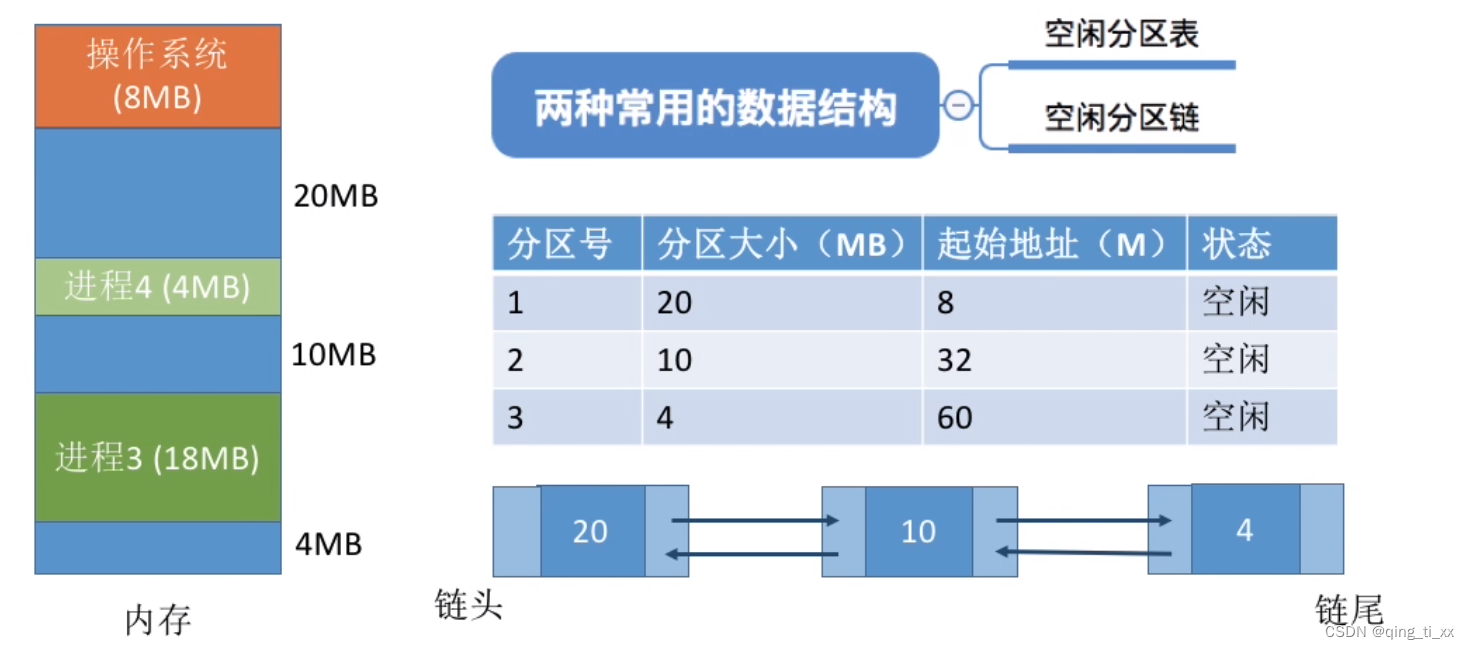
3、两种常用的数据结构:
(1)空闲分区表、空闲分区链
4、例子
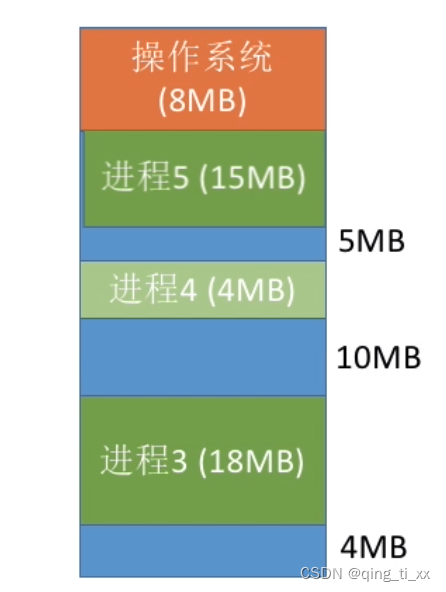
(1)假设我们要插入一个大小为15MB的内存,它会比较空闲区的大小,第一次遇到的空闲区为20MB,所以直接放入。
二、最佳适应算法
1、算法思想:
由于动态分区分配是一种连续分配方式,为各进程分配的空间必须是连续的一整片区域。因此为了保证当“大进程”到来时能有连续的大片空间,可以尽可能多地留下大片的空闲区,即,优先使用更小的空闲区。
2、如何实现:
空闲分区按容量递增次序链接。每次分配内存时顺序查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
3、例子:

(1)若我们要插入一个为9MB的进程,就从小到大找空闲区。
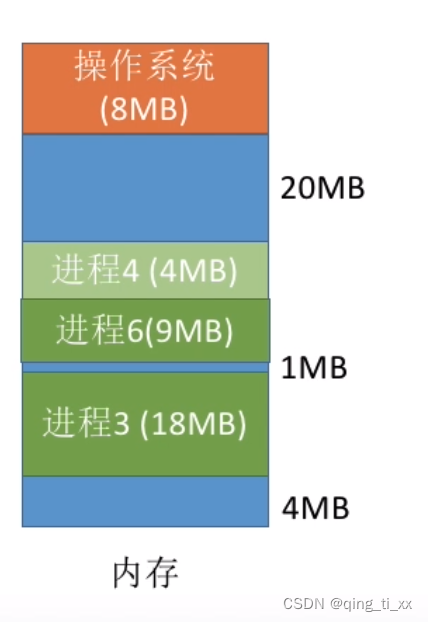
(2)插入后,我们要重新对空闲区链表进行排序

三、最坏适应算法
1、算法思想:
算法思想:为了解决最佳适应算法的问题――即留下太多难以利用的小碎片,可以在每次分配时优先使用最大的连续空闲区,这样分配后剩余的空闲区就不会太小,更方便使用。
2、如何实现:
空闲分区按容量递减次序链接。每次分配内存时顺序查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
3、例子
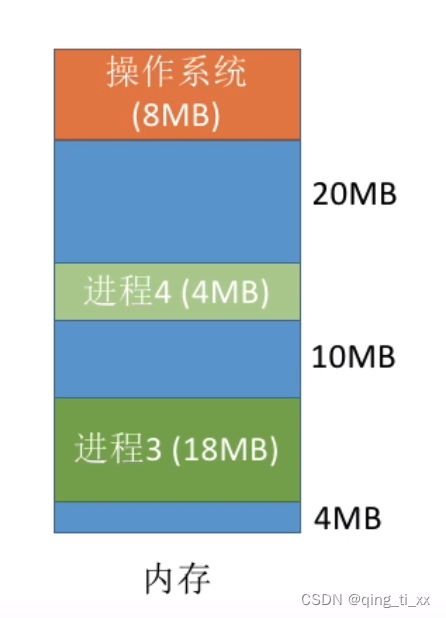
(1)我们要将大小为3MB的进程插入内存,找到最大的空闲区并存入
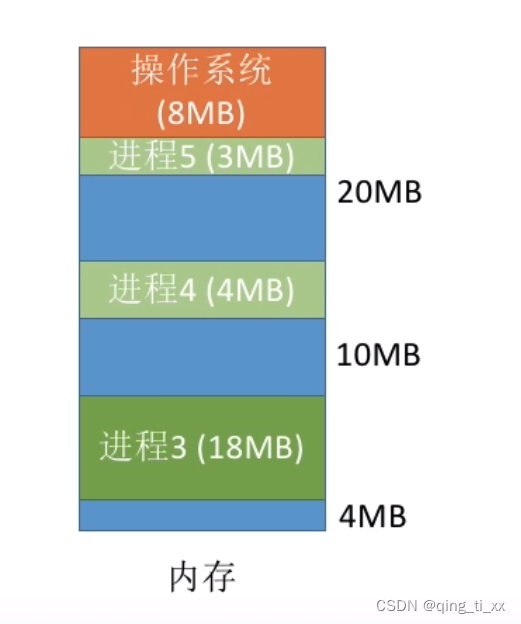
4、缺点
每次都选最大的分区进行分配,虽然可以让分配后留下的空闲区更大,更可用,但是这种方式会导致较大的连续空闲区被迅速用完。如果之后有“大进程”到达,就没有内存分区可用了。
四、临近适应算法
算法思想:
首次适应算法每次都从链头开始查找的。
这可能会导致低地址部分出现很多小的空闲分区,而每次分配查找时,都要经过这些分区,因此也增加了查找的开销。
如果每次都从上次查找结束的位置开始检索,就能解决上述问题。
如何实现:
空闲分区以地址递增的顺序排列((可排成一个循环链表)。
每次分配内存时从上次查找结束的位置开始查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
五、总结