动态规划的数组压缩技巧 - 机器人走格子问题
题目是leetcode62题目原题 表示如下
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?

递归版本
我们首先来想递归函数的含义 它会返回给我们一个int类型的数据 这个数据就是我们的最大路径数
我们需要给这个函数 我们当前的位置 我们需要去到的位置 整体函数如下
int _uniquePaths(int x , int y ,int m , int n)
其中 x y 代表我们当前位置的坐标 m n代表要到达位置的坐标
接下来我们想base case
因为这是一个位置限制的棋盘 所以说我们要考虑是否会越界的问题 即
if (x > m || y > n)
{
return 0;
}
当然 当我们的走到finish位置的时候也算是结束了 会返回给我们一种路径方法 表示如下
if (x == m && y == n)
{
return 1;
}
接下来我们就开始列举各种可能性 因为我们这里只能往下或者是往右走 所以说一共有两种可能性
我们只需要把这两种可能性所需要的路径和相加就可以了 代码表示如下
int _uniquePaths(int x , int y ,int m , int n)
{
// base case
if (x > m || y > n)
{
return 0;
}
if (x == m && y == n)
{
return 1;
}
int p1 = _uniquePaths(x + 1 , y, m, n);
int p2 = _uniquePaths(x, y + 1, m, n);
return p1 + p2;
}
动态规划
接下来我们开始动态规划版本的代码改写
首先我们找出一直变化的变量是什么
int _uniquePaths(int x , int y ,int m , int n)
我们发现递归中一直变化的参数其实只有两个 x 和 y
所以说我们只需要建立一张x和y的二维表就可以
x的格子一共有m个 y的格子一共有n个 所以说 x的大小可以设置为 0 ~ m-1 y的大小可以设置为0 ~ n-1
我们要知道的是 x和y可能会越界 所以说我们要设置一个pickup函数来从表中选值 如果说越界了我们直接返回0即可
int pickup_dp(int x , int y , int m , int n , vector<vector<int>>& dp)
{
if (x > m || y > n)
{
return 0;
}
return dp[x][y];
}
接下来我们来看base case
if (x == m && y == n)
{
return 1;
}
也就是说 当x为最大值 y为最大值的时候 此时dp表设置为1
dp[m-1][n-1] = 1;
接下来我们开始找位置依赖关系
int p1 = _uniquePaths(x + 1 , y, m, n);
int p2 = _uniquePaths(x, y + 1, m, n);
假设这个格子是表中任意一个 图中表示为黑色的格子

那么依赖的格子就是红色的
根据依赖关系 我们可以从右往左 从下往上的方式 来填写依赖关系 代码表示如下
int dp_uniquePaths(int m , int n , vector<vector<int>>& dp)
{
dp[m-1][n-1] = 1;
for (int col = n -1 ; col >= 0 ; col--)
{
for (int row = m -1; row >= 0; row--)
{
if (row == m-1 && col == n-1)
{
continue;
}
int p1 = pickup_dp(row + 1, col, m, n, dp);
int p2 = pickup_dp(row , col + 1, m, n, dp);
dp[row][col] = p1 + p2;
}
}
return dp[0][0];
}
这就是这道题目的动态规划解法
数组压缩技巧
我们可以发现的是 其实每个格子都只依赖于该列和它的右边一列 那么我们就可以使用两个列来表示整个二维表
也就是二维表转化为一维表 节省一定的空间
压缩技巧也很简单 只需要一列一列的转化就可以
代码表示如下
class Solution {
public:
int pickup_dp(int x , int m , vector<int>& dp)
{
if (x >= m || x < 0)
{
return 0;
}
return dp[x];
}
int dp_uniquePaths(int m , int n )
{
// col1 prev
// col2 cur
vector<int> col1(m , 0);
vector<int> col2(m , 0);
col1[m-1] = 1;
for (int i = 0; i < n ; i++)
{
for(int j = m - 1; j >= 0; j--)
{
col2[j] = pickup_dp(j + 1, m, col2) + col1[j];
}
for(int j = m -1 ; j >= 0 ; j--)
{
col1[j] = col2[j];
}
}
return col2[0];
}
int uniquePaths(int m, int n)
{
return dp_uniquePaths(m , n );
}
};
我们这里稍微讲解下两列的转化思路
我们设定 col1为前一列 col2为当前列
每次我们修改col2内部的值 到最后我们全部修改完毕要到下一列的时候 我们更新下col1列的所有值
钱包问题一
我们给定一个数组 arr 数组里面的值表示任意一张面值的钞票
每张钞票代表的值可能相同 但是我们认为它们是不同的钞票
现在我们给定一个 val 值 请问有多少种组合方案可以让val值为0
递归解法
还是一样 我们首先来想函数
它要返回给我们一个组合的最大值 所以说我们的返回值要是一个int类型的数值
我们要遍历整个money数组 所以说我们需要这个数组和一个index参数来遍历
接着我们需要一个rest参数来记录剩余零钱的数目
整体函数如下
int process(vector<int>& money , int index , int rest)
接下来我们开始想base case
这道题目中有两个变化的量 我们首先向有没有可能会因为index而终止递归呢?
当然有 如果index越界了 那么我们的递归也就终止了
有没有可能因为rest而终止递归呢 ?
当然有 如果剩余零钱的数目为0 我们就终止递归了
if (rest < 0)
{
return 0;
}
int N = static_cast<int>(money.size());
if (index == N)
{
return rest == 0 ? 1 : 0;
}
接下来开始列举可能性 对于这种从左往右的模型来说 可能性就是要和不要两种情况
所以说我们直接列出这两种可能性之后想加即可
int process(vector<int>& money , int index , int rest)
{
if (rest < 0)
{
return 0;
}
int N = static_cast<int>(money.size());
if (index == N)
{
return rest == 0 ? 1 : 0;
}
int p1 = process(money , index + 1 , rest);
int p2 = process(money , index +1 , rest - money[index]);
return p1 + p2;
}
动态规划
我们首先观察递归函数
int process(vector<int>& money , int index , int rest)
我们可以发现 其中变化的变量有 index 和 rest
所以说我们可以围绕着index 和 rest建立一张二维表
index 的大小是 0 ~ index 大小是index + 1
rest 的大小是 0 ~ rest 大小是rest + 1
我们建立完一个二维表之后就可以根据base case填写数据了
根据
if (index == N)
{
return rest == 0 ? 1 : 0;
}
我们可以得出
dp[N][0] = 1;
接着我们来看位置依赖关系

它依赖于下面一行的两个格子
所以说我们从最下面的倒数第二行开始填写数据 为了防止越界问题 我们再写一个pickup函数
完整代码如下
int dpprocess(vector<int>& money , int rest)
{
int N = static_cast<int>(money.size());
vector<vector<int>> dp(N + 1 , vector<int>(rest + 1 , 0));
dp[N][0] = 1;
for (int row = N - 1; row >= 0; row--)
{
for (int col = 0; col <= rest; col++)
{
dp[row][col] = pickupdp(row + 1 , col , dp , N , rest) + pickupdp(row + 1 , col - money[row] , dp , N , rest);
}
}
return dp[0][rest];
}
钱包问题二
我们给定一个数组 arr 数组里面的值表示任意一张面值的钞票 arr内部值不同
每一个arr中的元素代表有无数张钞票
现在我们给定一个 val 值 请问有多少种组合方案可以让val值为0
这个问题和问题一的区别就是 在问题2中 我们的钱包有无数张钞票 只是它们的面值不同 要我们求解法
递归版本
我们首先来想 我们要写什么样的一个递归函数
我们要让这个函数返回一个最大的组合方案 所以返回值是一个int类型的数据
而我们要在一个数组中选取数据 所以自然而然的想到使用index遍历
最后我们还需要一个rest来表示剩余值 整体表示如下
int process(vector<int>& money , int index , int rest)
接着就是想base case 这一步照抄钱包问题一即可
到了列举可能性的这一步就有点意思了
此时的问题就从要不要变为了两个问题
- 要不要?
- 要的话要几个
所以说我们的代码也要转变下
int p1 = process(money , index + 1 , rest);
// how many ?
int p2 = 0;
for (int fix = 1 ; fix * money[index] <= rest; fix++)
{
p2 += process(money , index + 1 , rest - fix * money[index]);
}
可能性1就是我们不要这种类型的钞票了
可能性2就是我们要这种类型的钞票 一张张枚举 知道rest小于0为止
当然我们其实可以让fix从0开始 这样就不需要可能性1了
整体代码表示如下
int process(vector<int>& money , int index , int rest)
{
if (rest < 0)
{
return 0;
}
int N = static_cast<int>(money.size());
if (index == N)
{
return rest == 0 ? 1 : 0;
}
int p1 = process(money , index + 1 , rest);
// how many ?
int p2 = 0;
for (int fix = 1 ; fix * money[index] <= rest; fix++)
{
p2 += process(money , index + 1 , rest - fix * money[index]);
}
return p1 + p2;
}
动态规划
我们首先观察递归函数
int process(vector<int>& money , int index , int rest)
我们可以发现 变量只有index 和rest
所以我们可以围绕着index和rest来做一张二维表
index 的大小是 0 ~ index 大小是index + 1
rest 的大小是 0 ~ rest 大小是rest + 1
我们建立完一个二维表之后就可以根据base case填写数据了
根据
if (index == N)
{
return rest == 0 ? 1 : 0;
}
我们可以得出
dp[N][0] = 1;
接下来我们来看为止依赖关系

我们可以发现这个位置依赖于下面一行的数据具体的格子数目不确定
所以说我们就可以写出这样子的代码
for (int row = N - 1; row >= 0; row--)
{
for(int col = 0; col <= rest; col++)
{
int ways = 0;
for (int fix = 0; fix * money[row] <= rest; fix++)
{
ways += pickupdp(row + 1 , col - fix * money[row] , dp , N , rest );
}
dp[row][col] = ways;
}
}
动态规划优化
我们还是来观察下图
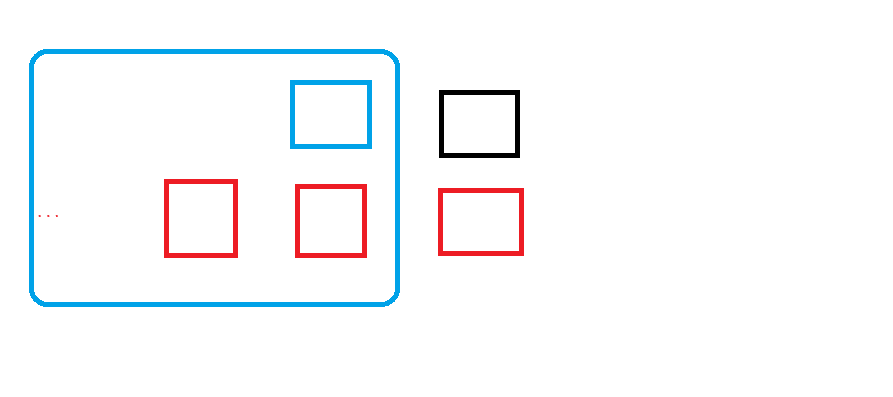
我们可以发现蓝色格子依赖的红色格子其实只比黑色格子依赖的红色格子少一个
也就是说我们可以这么转化
黑色格子依赖于蓝色格子和它下面的一个红色格子
于是我们的代码就可以这样子改写
int dpprocess(vector<int>& money , int rest)
{
int N = static_cast<int>(money.size());
vector<vector<int>> dp(N + 1 , vector<int>(rest + 1 , 0));
dp[N][0] = 1;
for (int row = N - 1; row >= 0; row--)
{
for(int col = 0; col <= rest; col++)
{
dp[row][col] = pickupdp(row , col - money[row] , dp , N ,rest) + pickupdp(row + 1 , col , dp , N , rest);
}
}
return dp[0][rest];
}
这样子我们就把原来的三个for循环优化成为了两个for循环 效率提高了不少
钱包问题三
我们给定一个数组 arr 数组里面的值表示任意一张面值的钞票 arr内部有相同值的钞票 我们认为值相同的钞票位置可以随意替换 (和题目一不同 题目一中每张钞票都是不同的 )
现在我们给定一个 val 值 请问有多少种组合方案可以让val值为0
这问题其实是题目二的变形
这里我提供一种思路将其转化为题目二 具体的代码大家可以自己尝试下
我们统计有多少种不同的钞票 并且将这些钞票添加到一个数组中
统计每个钞票的数目 再做一个数组
其中 第一个数组的用途和钱包问题二中的用途一样 而第二个数组则约束了每张钞票最多能取多少
之后按照钱包问题二的思路去做即可