【真题T1】[NOIP2022] 种花

news2024/11/25 0:24:12

一.题目

P8865 [NOIP2022] 种花 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

二.思路（80pts）

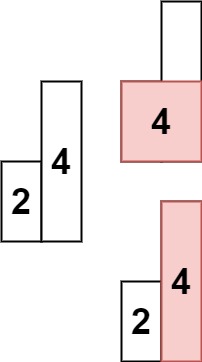
（1）"C"型

则我们可以计算出每一行的前缀和，然后枚举每一列
再每枚举每一行，定义为x1；
在x1的基础上往下枚举，找出x2.则"C"型就成型了。

（2）“F”型

计算每一列的前缀和，就在“C“型的基础上，再乘以x2的列前缀和，即x2以下还有几个格子。

（3）代码

#include<bits/stdc++.h>
#define maxn 1005
#define mod 998244353
using namespace std;
char s[maxn][maxn];
int f[maxn][maxn],g[maxn][maxn]; //前缀和 
long long ansc,ansf;
int main(){
	int T,id,n,m,ccc,fff;
	scanf("%d%d",&T,&id);
	while(T--){
		//初始化 
		ansc=0; ansf=0;
		scanf("%d%d%d%d",&n,&m,&ccc,&fff);
		for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
		//前缀和 
        for(int i=1; i<=n;i++){
            f[i][m + 1]=0;
            for(int j=m;j>=1;j--) {
                f[i][j]=s[i][j]=='0' ? 1+f[i][j + 1] : 0;
            }
        }
        for(int j=1; j<=m;j++) {
            g[n+1][j]=0;
            for(int i=n; i>=1;i--) {
                g[i][j]=s[i][j]=='0' ? 1+g[i + 1][j] : 0;
            }
        }
		//work
		for(int j=1;j<=m;j++){ //枚举每一列 
			for(int i=1;i<=n-2;i++){  //x1
				if(s[i][j]=='1') continue;
				for(int k=i+2;k<=n;k++){  //x2 
					if(s[k-1][j]=='1') break;
					ansc = (ansc + max(0,f[i][j]-1) * max(0,f[k][j]-1) % mod) % mod;
					ansf = (ansf + max(0,f[i][j]-1) * max(0,f[k][j]-1) * max(0,g[k][j]-1) % mod) % mod;
				}
			}
		}
		printf("%lld %lld\n",ansc*ccc,ansf*fff);
	}
	return 0;
}

三.优化（100pts）

我们可以看出，枚举列的循环显然是无法优化的。但我们枚举了两次行，即x1，x2。这我们可以优化。我们只枚举x2即可。

我们发现，在枚举x2时，只需要x2*sum即可。sum就是x1的累加。

四.AC

#include<bits/stdc++.h>
#define maxn 1005
#define mod 998244353
using namespace std;
char s[maxn][maxn];
int f[maxn][maxn],g[maxn][maxn]; //前缀和 
long long ansc,ansf;
int main(){
	int T,id,n,m,ccc,fff;
	scanf("%d%d",&T,&id);
	while(T--){
		//初始化 
		ansc=0; ansf=0;
		scanf("%d%d%d%d",&n,&m,&ccc,&fff);
		for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
		//前缀和 
        for(int i=1; i<=n;i++){
            f[i][m + 1]=0;
            for(int j=m;j>=1;j--) {
                f[i][j]=s[i][j]=='0' ? 1+f[i][j + 1] : 0;
            }
        }
        for(int j=1; j<=m;j++) {
            g[n+1][j]=0;
            for(int i=n; i>=1;i--) {
                g[i][j]=s[i][j]=='0' ? 1+g[i + 1][j] : 0;
            }
        }
		//work
		for(int j=1;j<=m;j++){ //枚举每一列 
			long long sum=0; //优化x1
			 for(int i=3;i<=n;i++){
			 	if(s[i][j]=='1'){
			 		sum=0;
			 		i+=2;
			 		continue;
				 }
				 if(s[i-1][j]=='0') sum+=max(0,f[i-2][j]-1);
				 ansc = (ansc + sum * max(0,f[i][j]-1) % mod ) %mod;
				 ansf = (ansf + sum * max(0,f[i][j]-1) * max(0,g[i][j]-1) % mod ) %mod;
			 }
		}
		printf("%lld %lld\n",ansc*ccc,ansf*fff);
	}
	return 0;
}