前言

在浅水方程的离散及求解方法一篇中，我们学习了三角形网格各边通量值及源项的求解。但仍有一个问题没有解决：对于边界处的网格，模型边界对应的网格边的通量求解。
对此，我们借鉴王志力¹的研究，学习各类边界条件下，网格边的通量的求解。

处理边界条件的原则

对于浅水水域，常见的边界有水位边界与流量边界。在此，我们假设网格$i$的第$j$条边对应了模型的边界，设边界上的水位为$h_{ij}^{\ast }$，垂直（外法线方向）和平行网格边的流速为${\tilde{u}}_{ij}^{\ast }$和${\tilde{v}}_{ij}^{\ast }$。为简便起见，以下我们将$h_{ij}^{\ast }$简记为$h^{\ast }$，将${\tilde{u}}_{ij}^{\ast }$和${\tilde{v}}_{ij}^{\ast }$简记为${\tilde{u}}_L^{\ast }$和${\tilde{v}}_L^{\ast }$
根据一维方程的特征线理论，沿着特征线方向有特征不变量，最终会得到如下关系：
$${\tilde{u}}_L^{\ast }+2c_L=u^{\ast }+2c^{\ast }$$
上式即确定边界条件时所要满足的原则。其中，$c_L=\sqrt{g{h}_L}$，$c^{\ast }=\sqrt{g{h}^{\ast }}$。

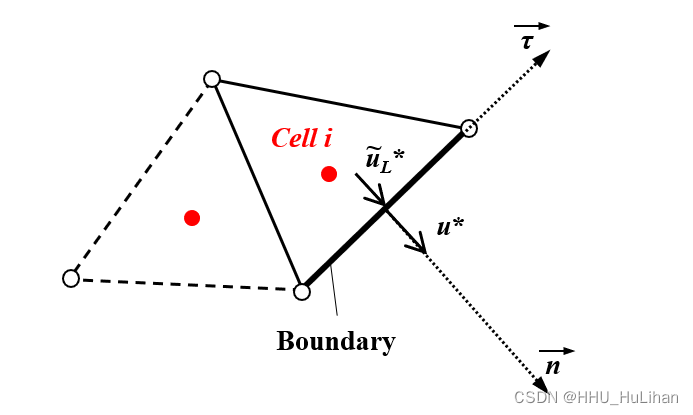
边界处水力要素的计算

在模型中，边界处的水力要素的计算步骤如下：

1. 根据笛卡尔坐标系下边界处的$u_L$和$v_L$转化为网格边界外法线方向和切向的${\tilde{u}}_L^{\ast }$和${\tilde{v}}_L^{\ast }$。
2. 给定边界处的$u^{\ast }$或$h^{\ast }$。此处的$u^{\ast }$值可通过流量边界条件转化而来。
3. 根据式${\tilde{u}}_L^{\ast }+2c_L=u^{\ast }+2c^{\ast }$来确定网格边上的其它变量。例如，对于水位条件，$h^{\ast }$已知，我们需要通过上式确定$u^{\ast }$。
4. 根据浅水方程的对流项确定通量值。

水位边界条件

对于边界条件，$h^{\ast }$已知，则：
$$u^{\ast }={\tilde{u}}_L^{\ast }+2c_L-2c^{\ast }={\tilde{u}}_L^{\ast }+2\sqrt{g{h}_L}-2\sqrt{g{h}^{\ast }}$$
之后将局部坐标系的$u^{\ast }$和$v^{\ast }$转化为全局笛卡尔坐标系下的$u_b$和$v_b$；记$h_b=h^{\ast }$。则边界处的通量为：
$$({\mathbf{F}}_n{)}_b=\mathbf{E}({\mathbf{U}}_{\mathbf{b}})n_x+\mathbf{G}({\mathbf{U}}_{\mathbf{b}})n_y=n_x\left(\begin{array}{c}h{u}_b\\ h{u}_b^2+\frac{g{h}_b^2}{2}\\ h{u}_b{v}_b\end{array}\right)+n_y\left(\begin{array}{c}h{v}_{b}z\\ h{u}_b{v}_b\\ h{v}_b^2+\frac{g{h}_b^2}{2}\end{array}\right)$$
式中，$(n_x,n_y)$表示边界处外法线方向。

单宽流量边界条件

给定网格边的单宽流量$q=h^{\ast }{u}^{\ast }$，则有：
$${\tilde{u}}_L^{\ast }+2c_L=u^{\ast }+2c^{\ast }=\frac{q}{h^{\ast }}+2\sqrt{g{h}^{\ast }}=\frac{q}{{c^{\ast }}^2/g}+2\sqrt{g{h}^{\ast }}$$
化简后，上述方程为$c^{\ast }$的一元三次方程：
$$2{c^{\ast }}^3-(u_L+2\sqrt{g{h}_L}){c^{\ast }}^2-gq=0$$
求解后可得$h^{\ast }={c^{\ast }}^2/g$。同理，我们可求得$h_b$、$u_b$和$v_b$，以及通量$({\mathbf{F}}_n{)}_b$。
注意：在设置边界时，我们需要设定单宽流量的方向；对于入流边界，单宽流量方向与边界外法线方向相反，则$q<0$；反之，对于出流边界，$q>0$。

流量边界条件

若流量给定在一个网格的边上，我们可以先求该边界的单宽流量$q$，之后按照上一小节等同的办法处理边界。若指定的边界条件涉及到m条连续的网格边（如下图边界蓝色边所示），组需要先求出每个对应网格边的单宽流量，之后再按单宽流量边界条件处理方法进行计算。

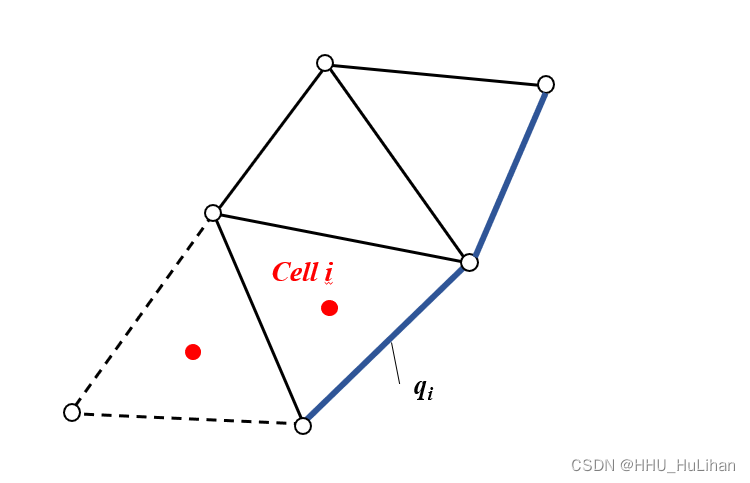
对于这m条边界上的总流量$Q$，某一网格$i$边上的单宽流量$q_i$是：
$$q_i=\frac{L_i^{\prime }{h}_i^{1.5}{C}_i}{{\sum }_{k=1}^m{L}_k^{\prime }{h}_k^{1.5}{C}_k}Q$$
式中，$L^{\prime }$表示流量边界对应网格边的边长，$h$表示对应网格的水深，$C$表示对应网格的摩阻力项，有$C=\frac{h^{1/6}}{n}$，n为曼宁系数。
之后根据求出的单款流量，依次处理每个边界网格的通量值。

固壁边界条件

在静止的固壁边界上，我们采用无滑移边界条件，即$u_b$和$v_b$均为0，故：
$$({\mathbf{F}}_n{)}_b=\left(\begin{array}{c}0\\ \frac{g{h}_L^2}{2}{n}_x\\ \frac{g{h}_L^2}{2}{n}_y\end{array}\right)$$

参考文献

---

1. 王志力. 基于Godunov和Semi-Lagrangian法的二、三维浅水方程的非结构化网格离散研究[D]. 辽宁:大连理工大学,2005. ↩︎