文章使用模块化(modular)的思想,分别从采样、训练、score network设计三个方面分析和改进diffusion-based models。
之前的工作1已经把diffusion-based models统一到SDE或者ODE框架下了,这篇文章的作者同样也从SDE和ODE的角度出发,不过换了一种SDE和ODE的表示形式。
假设有方差是
σ
d
a
t
a
\sigma_{data}
σdata的数据分布
p
d
a
t
a
(
x
)
p_{data}(\mathbf x)
pdata(x)。考虑一族分布
p
(
x
;
σ
)
p(\mathbf x; \sigma)
p(x;σ),其通过对数据添加方差为
σ
\sigma
σ的高斯噪声产生。在变化的过程中加入缩放
x
=
s
(
t
)
x
^
\mathbf x=s(t)\hat{\mathbf x}
x=s(t)x^,则有下面的ODE:
d
x
=
[
s
˙
(
t
)
s
(
t
)
x
−
s
(
t
)
2
σ
˙
(
t
)
σ
(
t
)
∇
x
log
p
(
x
s
(
t
)
;
σ
(
t
)
)
]
d
t
(4)
\mathrm{d} \mathbf x = \left[ \frac{\dot s(t)}{s(t)} \mathbf x - s(t)^2 \dot\sigma(t) \sigma(t) \nabla_{\mathbf x} \log p(\frac{\mathbf x}{s(t)}; \sigma(t)) \right] dt \tag{4}
dx=[s(t)s˙(t)x−s(t)2σ˙(t)σ(t)∇xlogp(s(t)x;σ(t))]dt(4)perturbation kernel的形式是:
p
0
t
(
x
(
t
)
∣
x
(
0
)
)
=
N
(
x
(
t
)
;
s
(
t
)
x
(
0
)
,
s
(
t
)
2
σ
(
t
)
2
I
)
(11)
p_{0t}(\mathbf x(t) | \mathbf x(0)) = \mathcal N(\mathbf x(t) ; s(t)\mathbf x(0), s(t)^2\sigma(t)^2 \mathbf I) \tag{11}
p0t(x(t)∣x(0))=N(x(t);s(t)x(0),s(t)2σ(t)2I)(11)在之前的工作1中SDE的形式是:
d
x
=
f
(
t
)
x
+
g
(
t
)
d
w
t
(10)
\mathrm{d} \mathbf x = f(t)\mathbf x + g(t)dw_t \tag{10}
dx=f(t)x+g(t)dwt(10)其中
s
(
t
)
=
exp
(
∫
o
t
f
(
ξ
)
d
ξ
)
s(t)=\exp(\int_o^t f(\xi)d\xi)
s(t)=exp(∫otf(ξ)dξ),
σ
(
t
)
=
∫
o
t
g
(
ξ
)
2
s
(
ξ
)
2
d
ξ
\sigma(t)=\sqrt{\int_o^t \frac{g(\xi)^2}{s(\xi)^2}d\xi}
σ(t)=∫ots(ξ)2g(ξ)2dξ。
不同于之前的论文,这篇文章考虑的是一个直接估计去噪输出的去噪函数
D
(
x
;
σ
)
D(\mathbf x;\sigma)
D(x;σ)。
E
y
∼
p
d
a
t
a
E
n
∼
N
(
0
,
σ
2
I
)
∥
D
(
y
+
n
;
σ
)
−
y
∥
2
2
,
∇
x
log
p
(
x
;
σ
)
=
(
D
(
x
;
σ
)
−
x
)
/
σ
2
(2,3)
\mathbb E_{y \sim p_{data}} \mathbb E_{\mathbf n \sim \mathcal N(\mathbf 0, \sigma^2 \mathbf I)} \| D(\mathbf y + \mathbf n;\sigma) - \mathbf y \|_2^2,~~~~\nabla_{\mathbf x}\log p(\mathbf x ; \sigma) = (D(\mathbf x; \sigma) - \mathbf x)/ \sigma^2 \tag{2,3}
Ey∼pdataEn∼N(0,σ2I)∥D(y+n;σ)−y∥22, ∇xlogp(x;σ)=(D(x;σ)−x)/σ2(2,3)其中
y
\mathbf y
y是训练样本,
n
\mathbf n
n是添加的噪声。在这种设置下,score function变成了用
D
(
x
;
σ
)
D(\mathbf x;\sigma)
D(x;σ)估计添加的噪声。用网络
D
θ
(
x
;
σ
)
D_\theta(\mathbf x;\sigma)
Dθ(x;σ)按照公式(2)可以估计
D
(
x
;
σ
)
D(\mathbf x;\sigma)
D(x;σ)。需要注意的是,
D
θ
(
x
;
σ
)
D_\theta(\mathbf x;\sigma)
Dθ(x;σ)可能包括额外的预处理步骤和后处理步骤。
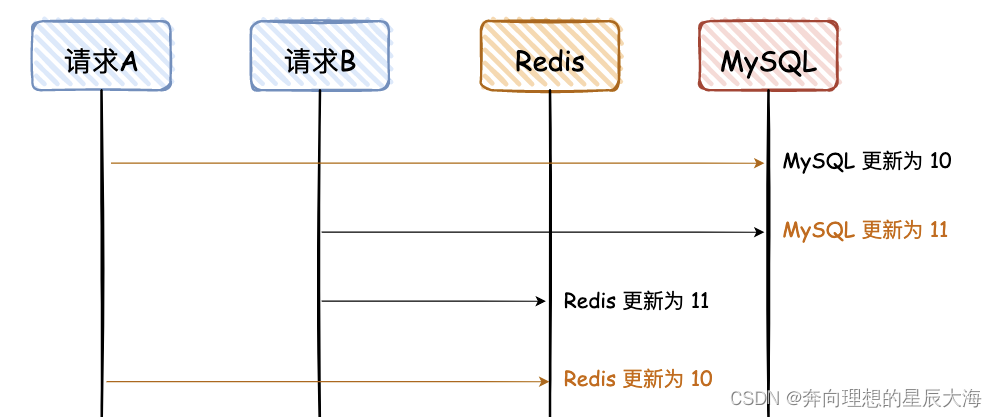
ODE解轨迹的形状由
σ
(
t
)
\sigma(t)
σ(t)和
s
(
t
)
s(t)
s(t)决定。因为在求解微分方程的时候截断误差(truncation error)和
d
x
/
d
t
dx/dt
dx/dt的曲率有关,作者认为最好的选择是
σ
(
t
)
=
t
\sigma(t)=t
σ(t)=t和
s
(
t
)
=
1
s(t)=1
s(t)=1,这样
d
x
/
d
t
=
(
x
−
D
(
x
;
t
)
)
/
t
dx/dt=(\mathbf x-D(\mathbf x;t))/t
dx/dt=(x−D(x;t))/t,并且
σ
\sigma
σ和
t
t
t是相同的,两个符号可以串着用。好处是在任何
x
,
t
x,t
x,t位置,一个到
t
=
0
t=0
t=0的Euler步就是对去噪图像的估计
D
θ
(
x
;
t
)
D_\theta(\mathbf x;t)
Dθ(x;t),解估计的切线总是指向去噪图像。如下图所示(c)也就是
σ
(
t
)
=
t
\sigma(t)=t
σ(t)=t和
s
(
t
)
=
1
s(t)=1
s(t)=1的情况,这和DDIM相同。
SDE可以表示成:
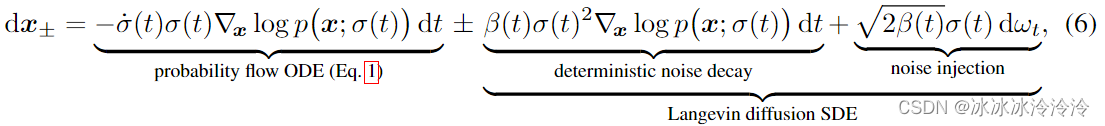
这揭示了为什么随机性在实践中有帮助:隐式朗之万扩散驱动样本在给定时间朝向所需的边际分布,主动纠正早期采样步骤中产生的任何错误。
直接用网络
D
θ
D_\theta
Dθ预测
D
(
x
;
σ
)
D(\mathbf x;\sigma)
D(x;σ)在实践中效果并不好,作者考虑对网络
F
θ
F_\theta
Fθ添加预处理步骤和后处理步骤来预测
D
(
x
;
σ
)
D(\mathbf x;\sigma)
D(x;σ)
D
θ
(
x
;
σ
)
=
c
s
k
i
p
(
σ
)
x
+
c
o
u
t
(
σ
)
F
θ
(
c
i
n
(
σ
)
x
;
c
n
o
i
s
e
(
σ
)
)
D_\theta(\mathbf x;\sigma)=c_{skip}(\sigma) \mathbf x + c_{out}(\sigma) F_\theta(c_{in}(\sigma)\mathbf x; c_{noise}(\sigma))
Dθ(x;σ)=cskip(σ)x+cout(σ)Fθ(cin(σ)x;cnoise(σ))

Score-Based Generative Modeling through Stochastic Differential Equations ↩︎ ↩︎



![[C++]:1.初识C++和C语言缺陷补充。](https://img-blog.csdnimg.cn/edad72d230224dca87297d99fd3d71c0.png)