一、概述

鲜奶会通过低温巴氏杀菌消灭有害物质同时保留活性生命物质，其对储存条件要求极为苛刻，保质期一般不超过15天，整个配送过程必须采用全程冷链方式（0~4°c冷藏环境），从澳洲每周直飞运往宁波或广州港，然后通过冷链运输车运往北京、杭州、上海的顺丰冷库，在顺丰冷运仓进行打包发货，本文介绍一下顺丰冷库系统的对接及打包发货配送全程跟踪。

二、顺丰冷库WMS系统对接

顺丰冷库WMS其实不是他们自己开发的，而是富勒提供开发与技术支持，叫做FLUX WMS,顺丰在每个仓储中心配有一个技术接口人。

系统主要对接以下几个接口

1、商品SKU上下架

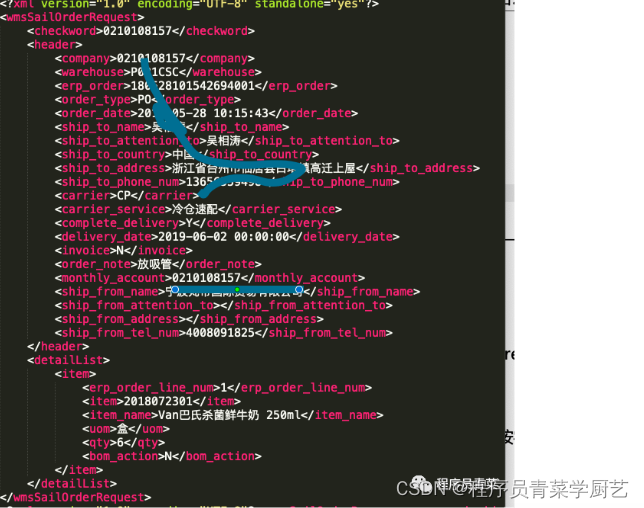
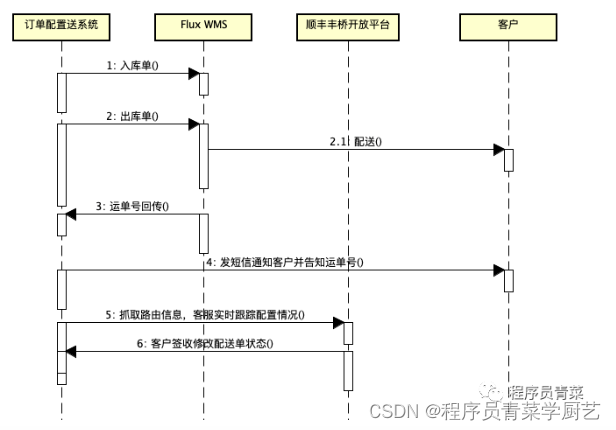
2、入库单推送：在冷链运输车到达之前推入库单到WMS，冷运库根据入库单接收货物。

3、配送单出库推送：最重要一个接口，因为鲜奶保质期短，一般在货物到达冷运仓第二、第三天要全部打包发货，否则鲜奶可能会变质。

4、运单回填：订单出库推送后WMS系统并不会立即返回运单号，需要等工人打包发货的时候才会生成运单号，这里有两种方式，一种是我们提供接口当顺丰运单号生成调我方接口回传，另外一种是我们定时遍历订单到WMS系统去查运单号。

5、路由信息：从顺丰丰桥开放平台获取路由信息。

6、实时库存接口

三、技术保障

1、因为每周鲜奶都集中在周五、周六两天配送，如果系统有一点问题没有及时配送出去，客户会有很大的情绪，鲜奶也可能会变质，技术上主要是针对推送的报文进行监测，开始是将报文放在单独的日志文件里，后来为了方便快速查询将报表丢到Redis里，报文是XML格式，采用JAXB来转换对象与XML数据以及格式化日志输出。

2、任何第三方系统都不是绝对可靠的，报文推送给Flux WMS，有时是因为报文格式不符合要求，有时候是顺丰仓对入库单没有确认，有时又是因为Flux WMS系统Bug或故障，所以能及时定位问题是相当重要的。

3、客服将配送单推往各个冷运仓，做一个报表，统计了推送的数量及运单号回传的数量对比，客服会实时关注，如果超过时间会及时联系冷仓管理人员安排打包。

4、客服在系统中能实时查看每一单当前配送在哪个节点，客户什么时候签收等信息，如果超过多长时间客户没有签收会及时跟进该配送单。