【LeetCode刷题（数据结构）】：给定一个链表返回链表开始入环的第一个节点如果链表无环则返回 NULL

news2024/11/28 8:27:32

在这里插入图片描述

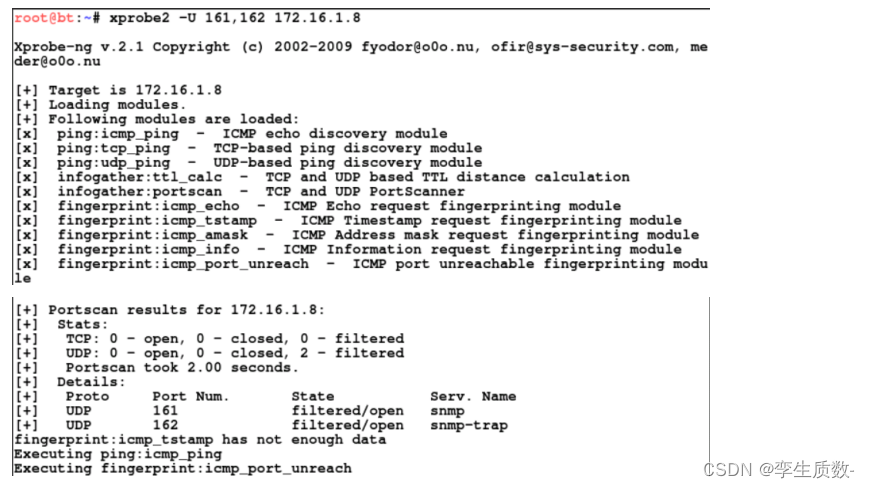
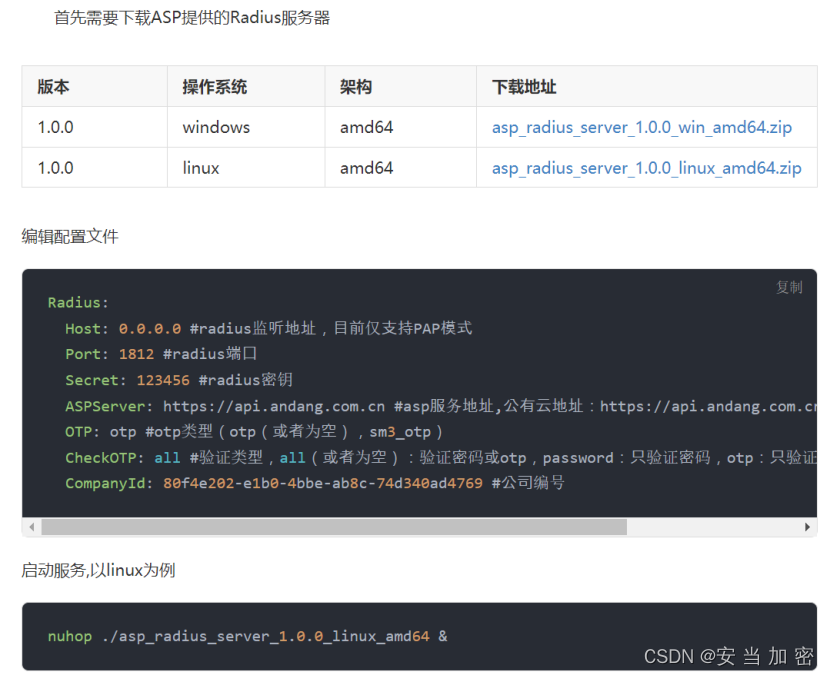
给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况
不允许修改链表
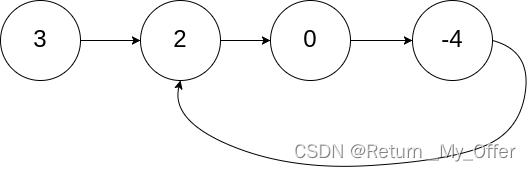
在这里插入图片描述
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点
在这里插入图片描述
输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环

方法：快慢指针

思路与算法
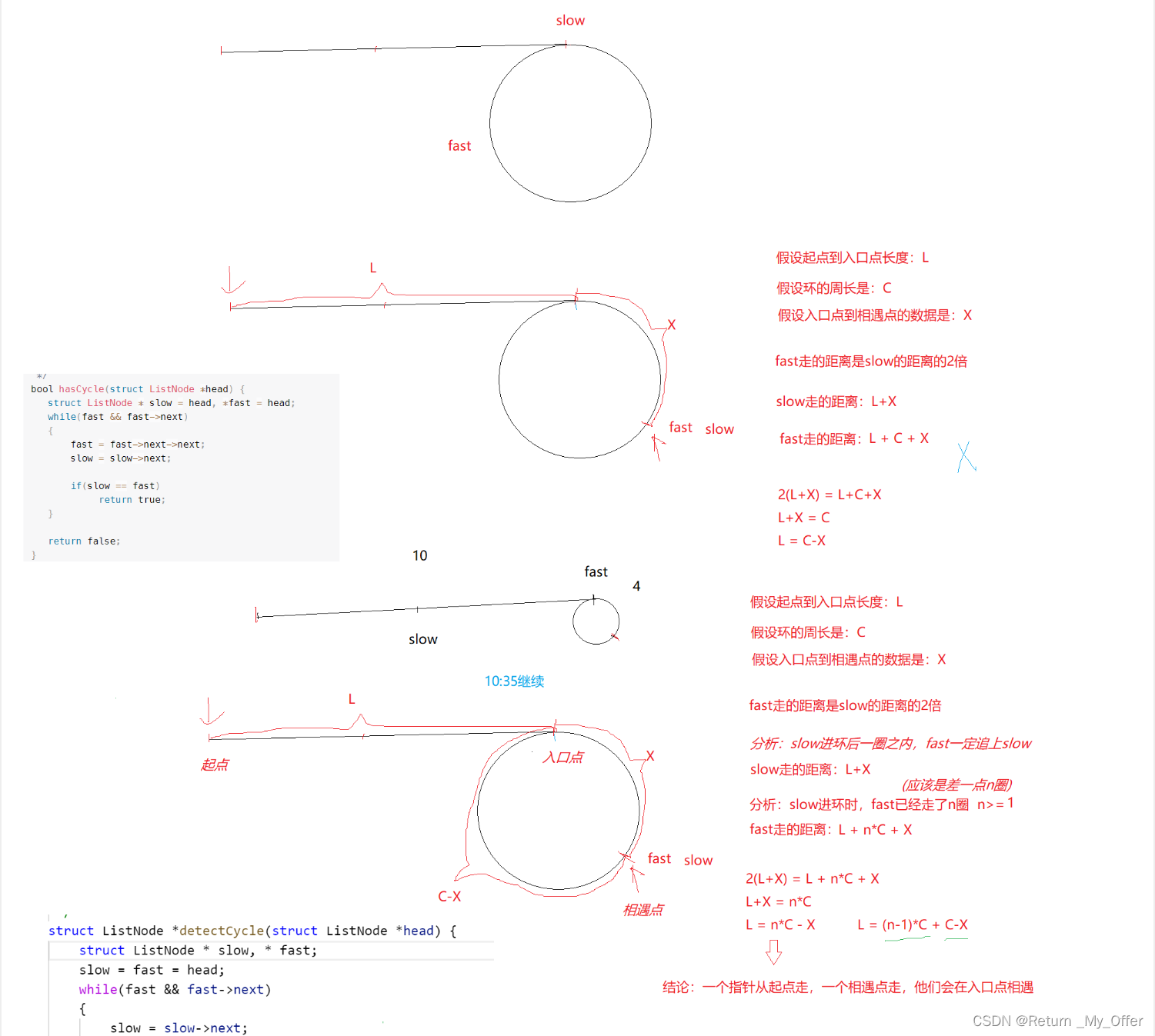
我们使用两个指针，fast\textit{fast}fast 与 slow\textit{slow}slow。它们起始都位于链表的头部。随后，slow\textit{slow}slow 指针每次向后移动一个位置，而 fast\textit{fast}fast 指针向后移动两个位置。如果链表中存在环，则 fast\textit{fast}fast 指针最终将再次与 slow\textit{slow}slow 指针在环中相遇
如下图所示，设链表中环外部分的长度为 aaa。slow\textit{slow}slow 指针进入环后，又走了 bbb 的距离与 fast\textit{fast}fast 相遇。此时，fast\textit{fast}fast 指针已经走完了环的 nnn 圈，因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nc
根据题意，任意时刻，fast\textit{fast}fast 指针走过的距离都为 slow\textit{slow}slow 指针的 222 倍。因此，我们有
a+(n+1)b+nc=2(a+b) ⟹ a=c+(n−1)(b+c)
有了 a=c+(n−1)(b+c) 的等量关系，我们会发现：从相遇点到入环点的距离加上 n−1n-1n−1 圈的环长，恰好等于从链表头部到入环点的距离
因此，当发现 slow\textit{slow}slow 与 fast\textit{fast}fast 相遇时，我们再额外使用一个指针 ptr\textit{ptr}ptr。起始，它指向链表头部；随后，它和 slow\textit{slow}slow 每次向后移动一个位置。最终，它们会在入环点相遇
图片讲解
在这里插入图片描述

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode*slow;
    struct ListNode*fast;
    slow=fast=head;
    while(fast&&fast->next)
    {
        while(fast&&fast->next)
        {
            slow=slow->next;
            fast=fast->next->next;
            if(slow==fast)
            {
                //结论//一个指针从起点走//一个指针从相遇点走//他们会在入口点相遇
                struct ListNode*meet=slow;//fast;//slow;
                while(head!=meet)
                {
                    meet=meet->next;
                    head=head->next;
                }
                return meet;
            }
        }
    }
    return NULL;
}