二分查找的详解

news2024/11/29 11:38:46

## 1.3 二分查找

二分查找算法也称折半查找，是一种非常高效的工作于有序数组的查找算法。后续的课程中还会学习更多的查找算法，但在此之前，不妨用它作为入门。

1) 基础版

需求：在**有序**数组 $A$ 内，查找值 $target$

* 如果找到返回索引
* 如果找不到返回 $-1$

算法描述

| | |
| ---- | ------------------------------------------------------------ |
| 前提 | 给定一个内含 $n$ 个元素的有序数组 $A$，满足 $A_{0}\leq A_{1}\leq A_{2}\leq \cdots \leq A_{n-1}$，一个待查值 $target$ |
| 1 | 设置 $i=0$，$j=n-1$ |
| 2 | 如果 $i \gt j$，结束查找，没找到 |
| 3 | 设置 $m = floor(\frac {i+j}{2})$ ，$m$ 为中间索引，$floor$ 是向下取整（$\leq \frac {i+j}{2}$ 的最小整数） |
| 4 | 如果 $target < A_{m}$ 设置 $j = m - 1$，跳到第2步 |
| 5 | 如果 $A_{m} < target$ 设置 $i = m + 1$，跳到第2步 |
| 6 | 如果 $A_{m} = target$，结束查找，找到了 |

> ***P.S.***
>
> * 对于一个算法来讲，都有较为严谨的描述，上面是一个例子
> * 后续讲解时，以简明直白为目标，不会总以上面的方式来描述算法

java 实现

* $i,j$ 对应着搜索区间 $[0,a.length-1]$（注意是闭合的区间），$i<=j$ 意味着搜索区间内还有未比较的元素，$i,j$ 指向的元素也可能是比较的目标
* 思考：如果不加 $i==j$ 行不行？
* 回答：不行，因为这意味着 $i,j$ 指向的元素会漏过比较
* $m$ 对应着中间位置，中间位置左边和右边的元素可能不相等（差一个），不会影响结果
* 如果某次未找到，那么缩小后的区间内不包含 $m$

### 2) 改变版

另一种写法

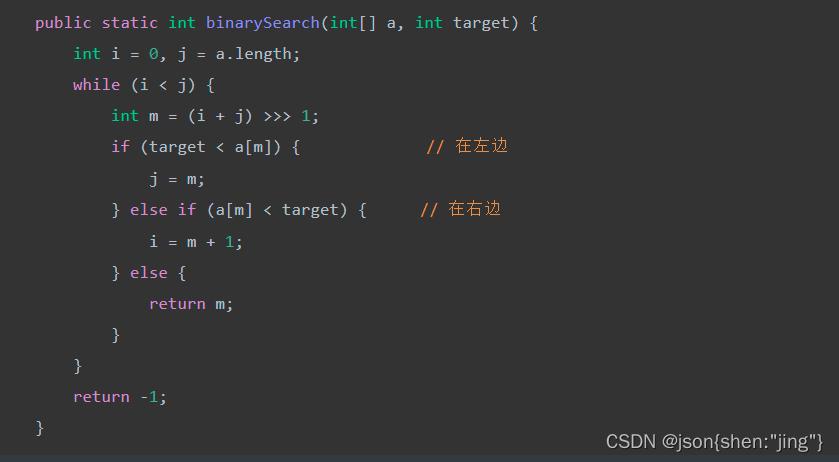
* $i,j$ 对应着搜索区间 $[0,a.length)$（注意是左闭右开的区间），$i<j$ 意味着搜索区间内还有未比较的元素，$j$ 指向的**一定不是**查找目标
* 思考：为啥这次不加 $i==j$ 的条件了？
* 回答：这回 $j$ 指向的不是查找目标，如果还加 $i==j$ 条件，就意味着 $j$ 指向的还会再次比较，找不到时，会死循环
* 如果某次要缩小右边界，那么 $j=m$，因为此时的 $m$ 已经**不是**查找目标了

1.4 衡量算法好坏

时间复杂度

下面的查找算法也能得出与之前二分查找一样的结果，那你能说出它差在哪里吗？

public static int search(int[] a, int k) {
    for (
        int i = 0;
        i < a.length;
        i++
    ) {
        if (a[i] == k) {
            return i;
        }
    }
    return -1;
}

考虑最坏情况下（没找到）例如 [1,2,3,4] 查找 5

int i = 0 只执行一次
i < a.length 受数组元素个数 $n$ 的影响，比较 $n+1$ 次
i++ 受数组元素个数 $n$ 的影响，自增 $n$ 次
a[i] == k 受元素个数 $n$ 的影响，比较 $n$ 次
return -1，执行一次

粗略认为每行代码执行时间是 $t$，假设 $n=4$ 那么

总执行时间是 $(1+4+1+4+4+1)*t = 15t$
可以推导出更一般地公式为，$T = (3*n+3)t$

如果套用二分查找算法，还是 [1,2,3,4] 查找 5

public static int binarySearch(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {            // 在左边
            j = m - 1;
        } else if (a[m] < target) {     // 在右边
            i = m + 1;
        } else {
            return m;
        }
    }
    return -1;
}

int i = 0, j = a.length - 1 各执行 1 次
i <= j 比较 $floor(\log_{2}(n)+1)$ 再加 1 次
(i + j) >>> 1 计算 $floor(\log_{2}(n)+1)$ 次
接下来 if() else if() else 会执行 $3* floor(\log_{2}(n)+1)$ 次，分别为
- if 比较
- else if 比较
- else if 比较成立后的赋值语句
return -1，执行一次