“理解梯度下降：直觉、数学公式和推导”

一、说明

梯度下降是机器学习中使用的一种流行的优化算法，通过迭代调整函数的参数来最小化函数。基本思想是将函数的参数沿函数梯度最陡峭下降的方向移动。

二、关于梯度的叙述

简单来说，想象一下你在山顶，你想尽快到达山脚下。你可以开始下坡，朝着感觉最陡的方向走几步。但是，您可能无法始终分辨出哪个方向真正最陡峭，尤其是在地形复杂的情况下。

相反，您可以使用一个工具来测量各个方向的地形陡度，例如指向下坡的指南针。使用此工具，您可以沿着指南针感觉最陡的方向迈出一小步，直到到达底部。梯度下降就像机器学习模型的指南针：它告诉模型如何调整其参数以最小化它试图优化的功能。

具体来说，梯度下降通过计算函数在当前点的梯度来工作，该梯度表示最陡峭的上升方向。然后，该算法朝着相反的方向迈出一小步，朝着最陡峭的下降方向迈出。这个过程重复了很多次，每一步的大小由学习率决定，直到算法达到最小值，因为我们的步长（学习率）正在减少。最初，我们的步长很高。

在机器学习中，正在优化的函数通常是一个成本函数，用于衡量模型在给定任务上的表现。通过使用梯度下降来最小化此成本函数，模型可以随着时间的推移提高其性能，学习做出更好的预测或分类。

以下是使用梯度下降在简单线性回归中查找 b 值的逐步数学公式和推导，假设我们已经有了 m 的值：

简单线性回归的方程是 y = mx + b，其中 y 是因变量，x 是自变量，m 是直线的斜率，b 是 y 截距。

假设我们有一组 n 个数据点（x1， y1），（x2， y2）， ...，（xn， yn），我们想找到最小化平方误差（SSE）之和的 m 和 b 值：

SSE = Σ（yi — （mx_i + b））²， i = 1 到 n

要使用梯度下降找到 b 的值，我们首先需要计算 SSE 相对于 b 的偏导数：

∂SSE/∂b = Σ-2（yi — （mx_i + b））

接下来，我们使用梯度下降更新规则更新 b 的值：

b_new = b — alpha * ∂SSE/∂b

其中阿尔法是学习率。我们重复这个过程，直到b的值收敛到最小值。

三、梯度如何实现

3.1 逐步推导：

将 b 初始化为随机值。
计算上证相对于b的梯度：
∂SSE/∂b = Σ-2（yi — （mx_i + b））
使用梯度下降更新规则更新 b：
b_new = b — alpha * ∂SSE/∂b
重复步骤 2 和 3，直到 b 的值收敛到最小值。

3.2 下面是一个使用梯度下降查找 b 值的 Python 代码示例：

from sklearn.datasets import make_regression
import numpy as np
X,y = make_regression(n_samples=4, n_features=1, n_informative=1, n_targets=1,noise=80,random_state=13)
import matplotlib.pyplot as plt
plt.scatter(X,y)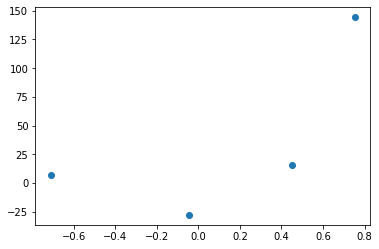

绘制散点图

# Lets apply OLS
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(X,y)
     
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
reg.coef_
     
>>>>>> array([78.35063668])
reg.intercept_
     
>>>>> 26.15963284313262
plt.scatter(X,y)
plt.plot(X,reg.predict(X),color='red')reg = LinearRegression()
reg.fit(X,y)
     
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
reg.coef_
     
>>>>>> array([78.35063668])
reg.intercept_
     
>>>>> 26.15963284313262
plt.scatter(X,y)
plt.plot(X,reg.predict(X),color='red')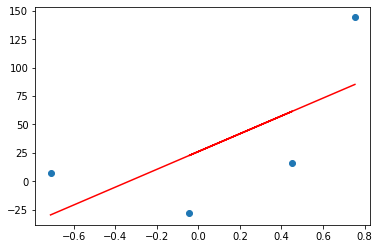

通过OLS方法进行线预测。

# Lets apply Gradient Descent assuming slope is constant m = 78.35
# and let's assume the starting value for intercept b = 0
y_pred = ((78.35 * X) + 100).reshape(4)
plt.scatter(X,y)
plt.plot(X,reg.predict(X),color='red',label='OLS')
plt.plot(X,y_pred,color='#00a65a',label='b = 0')
plt.legend()
plt.show()

m = 78.35
b = 100
loss_slope = -2 * np.sum(y - m*X.ravel() - b)
loss_slope
     
>>>> 590.7223659179078
# Lets take learning rate = 0.1
lr = 0.1
step_size = loss_slope*lr
step_size
     
>>>>> 59.072236591790784
# Calculating the new intercept
b = b - step_size
b
     
>>>> 40.927763408209216
y_pred1 = ((78.35 * X) + b).reshape(4)
plt.scatter(X,y)
plt.plot(X,reg.predict(X),color='red',label='OLS')
plt.plot(X,y_pred1,color='#00a65a',label='b = {}'.format(b))
plt.plot(X,y_pred,color='#A3E4D7',label='b = 0')
plt.legend()
plt.show()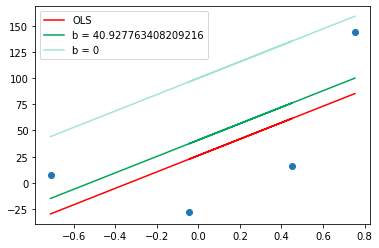

Comparison different values of b

# Iteration 2
loss_slope = -2 * np.sum(y - m*X.ravel() - b)
loss_slope
     
>>>>> 118.14447318358157
step_size = loss_slope*lr
step_size
     
>>>>> 11.814447318358157
b = b - step_size
b
     
>>>>> 29.11331608985106
y_pred2 = ((78.35 * X) + b).reshape(4)
plt.scatter(X,y)
plt.plot(X,reg.predict(X),color='red',label='OLS')
plt.plot(X,y_pred2,color='#00a65a',label='b = {}'.format(b))
plt.plot(X,y_pred1,color='#A3E4D7',label='b = {}'.format(b))
plt.plot(X,y_pred,color='#A3E4D7',label='b = 0')
plt.legend()
plt.show()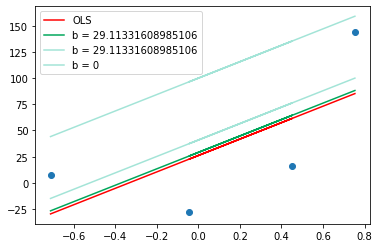

loss_slope = -2 * np.sum(y - m*X.ravel() - b)
loss_slope
     
>>>> 23.62889463671634
step_size = loss_slope*lr
step_size
     
>>>> 2.362889463671634
b = b - step_size
b
     
>>>> 26.750426626179426
y_pred3 = ((78.35 * X) + b).reshape(4)
plt.figure(figsize=(15,15))
plt.scatter(X,y)
plt.plot(X,reg.predict(X),color='red',label='OLS')
plt.plot(X,y_pred3,color='#00a65a',label='b = {}'.format(b))
plt.plot(X,y_pred2,color='#A3E4D7',label='b = {}'.format(b))
plt.plot(X,y_pred1,color='#A3E4D7',label='b = {}'.format(b))
plt.plot(X,y_pred,color='#A3E4D7',label='b = 0')
plt.legend()
plt.show()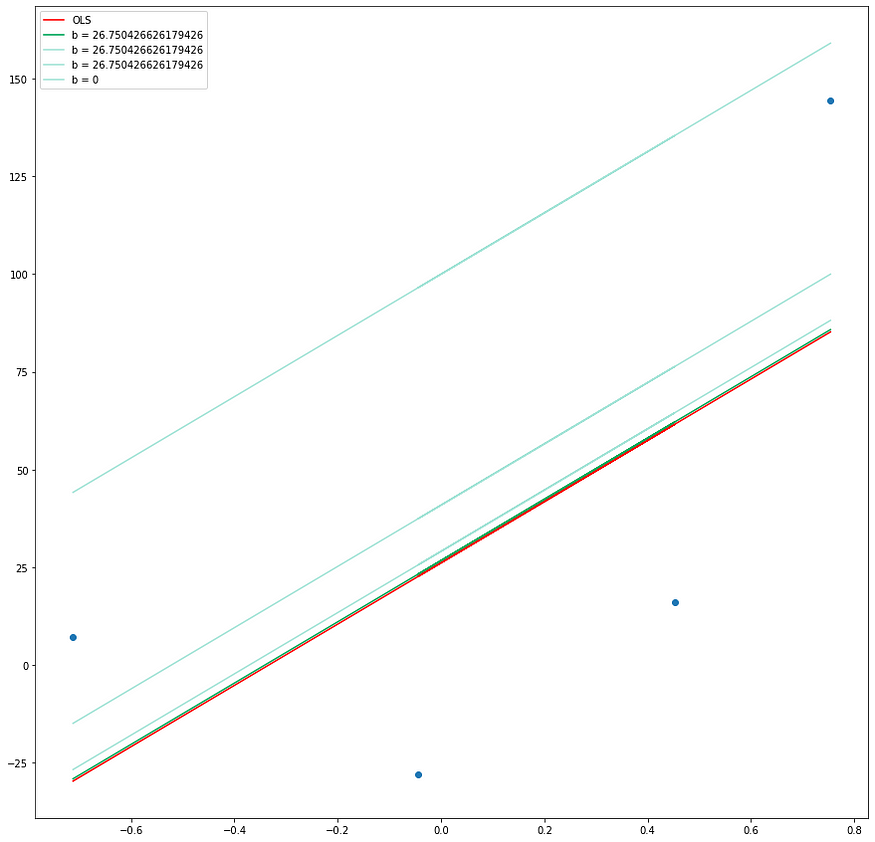

b = -100
m = 78.35
lr = 0.01
epochs = 100
for i in range(epochs):
  loss_slope = -2 * np.sum(y - m*X.ravel() - b)
  b = b - (lr * loss_slope)
  y_pred = m * X + b
  plt.plot(X,y_pred)
plt.scatter(X,y)

四、“可视化梯度下降：查找 y 截距的分步示例。”

4.1 最佳贴合线：

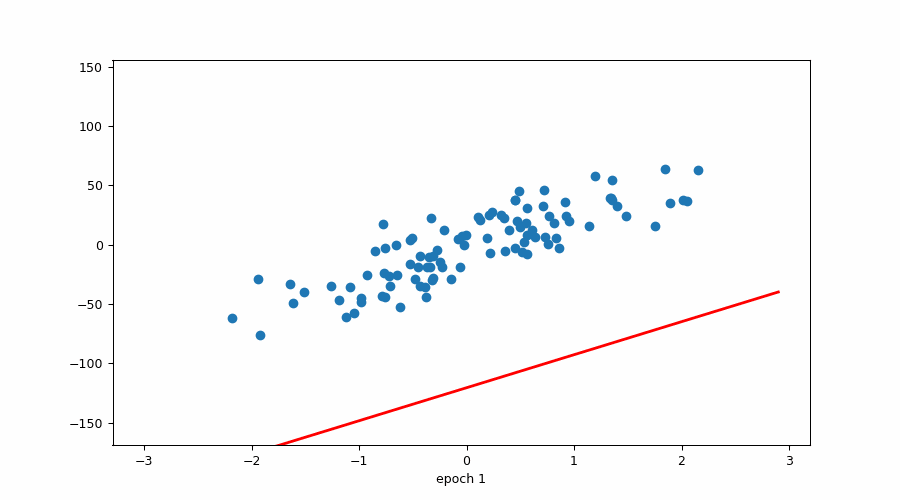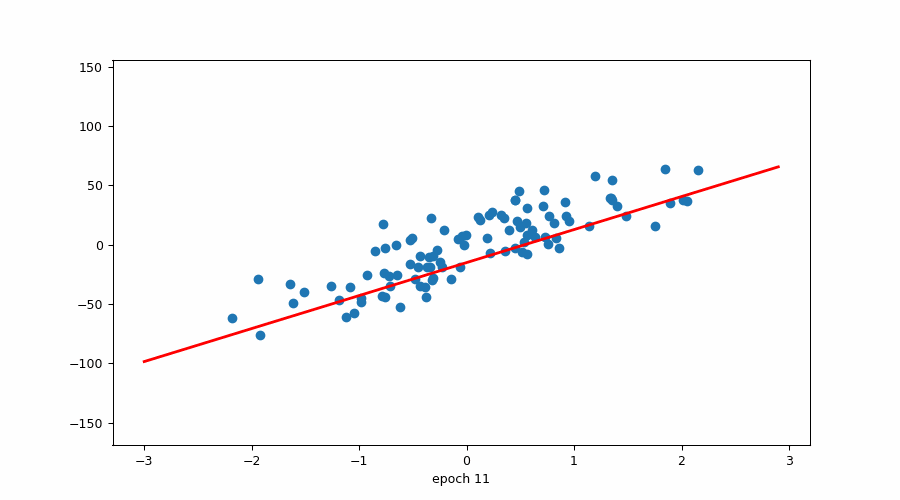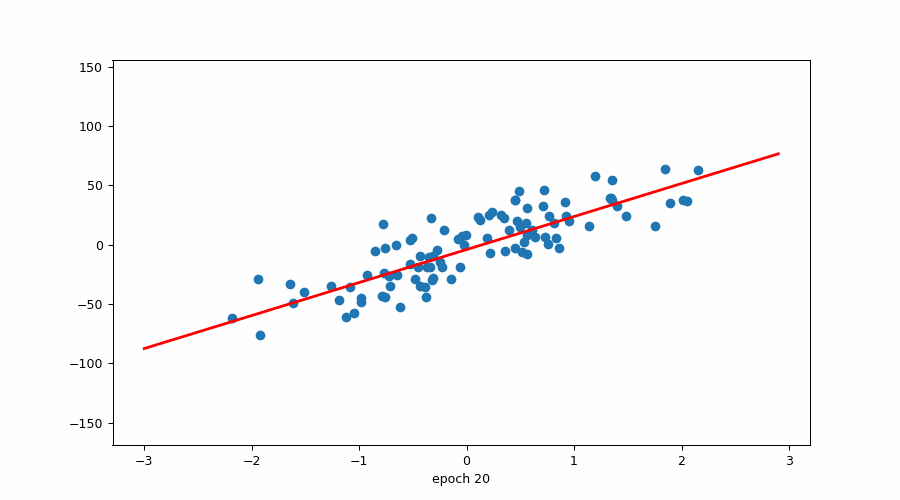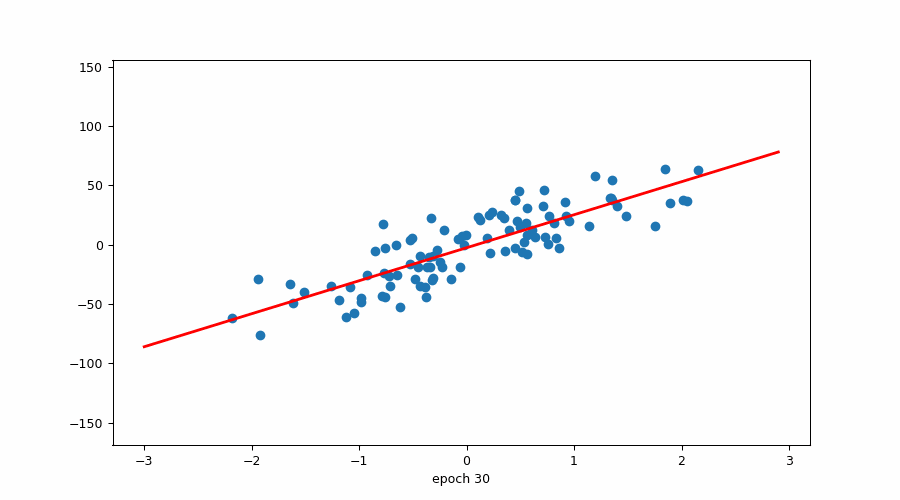
当我们已经有斜率时试图找到 b（截距）

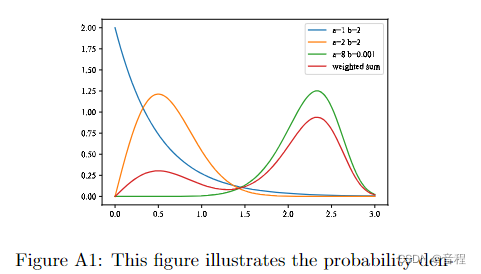
4.2 该图说明了周期数与损失之间的关系。

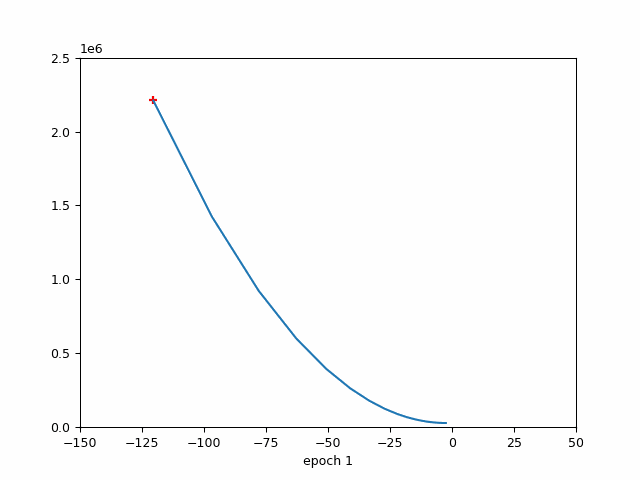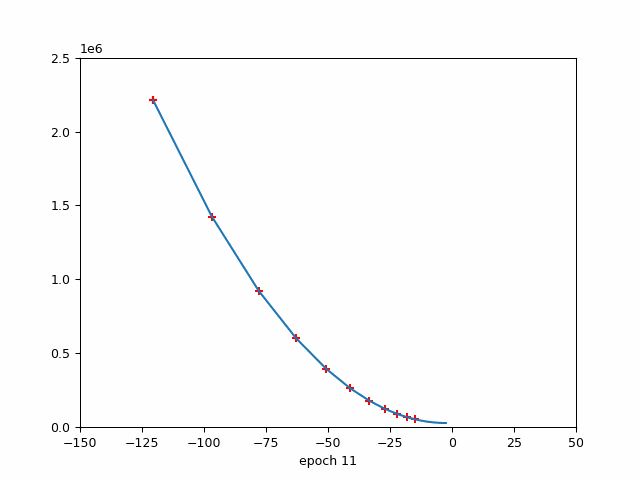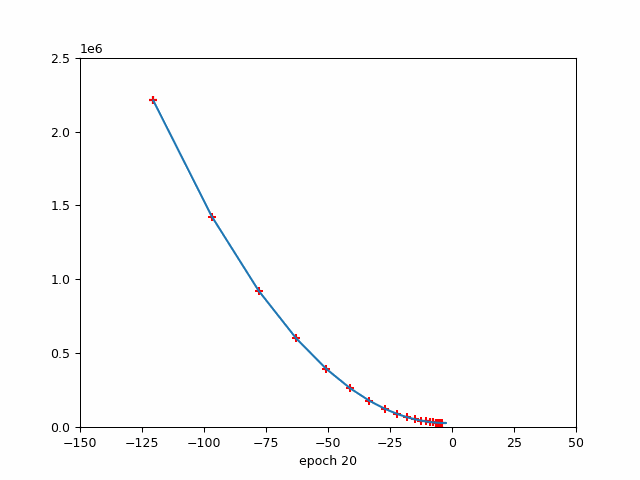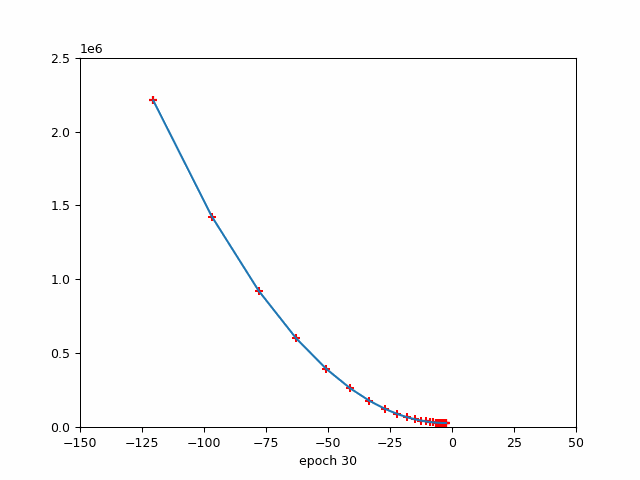
损失与时期（红色标记→学习率）

损失与时期

该图说明了 epoch 数与损失之间的关系，同时还指示了优化算法中使用的学习率。随着 epoch 数量的增加，损失会减少，这表明模型正在学习并提高其在任务上的性能。但是，重要的是要注意，在整个训练过程中，学习率并不是恒定的。

在训练开始时，学习率很高，这使得模型能够对其参数进行大量更新，并迅速收敛到损失函数的最小值。当模型接近最小值时，学习率会降低，以避免超过最小值并确保更稳定的收敛。

4.3 学习率。

学习率是一个超参数，用于控制梯度下降算法每次迭代中执行的步骤的大小。如果学习率太低，算法可能会收敛缓慢，而如果学习率太高，算法可能会超过最小值并发散。

以下是不同学习率如何影响梯度下降的图表表示：

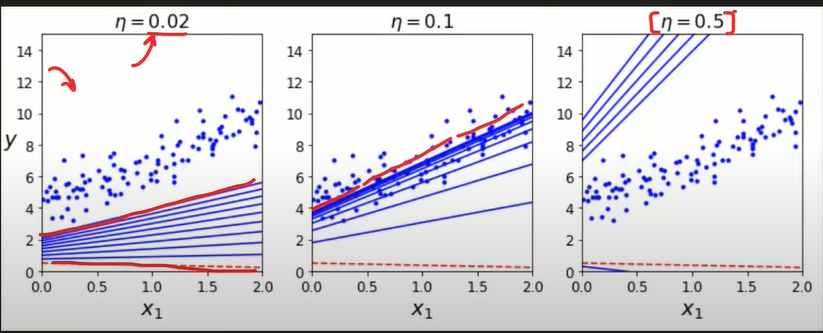
在图中，我们有一个简单的 2D 成本函数，只有一个最小值。蓝点代表数据点，蓝线是我们具有不同学习率的梯度下降算法的最佳拟合线。

在左边，我们的学习率很低。该算法沿梯度方向采取小步骤，并缓慢收敛到最小值。

在中间，我们的学习率适中。该算法采用更大的步骤，并更快地收敛到最小。

在右边，我们的学习率很高。该算法采取非常大的步骤并超过最小值，导致算法在最小值附近发散和振荡。

为手头的特定问题选择合适的学习率很重要，因为不同的问题可能有不同的最佳学习率。一种常见的方法是尝试不同的学习率并观察算法的收敛行为。

减少损失：优化学习率 |机器学习 |谷歌开发者

4.4 逐步数学公式和推导，用于使用梯度下降在简单线性回归中查找 m 和 b 的值：

简单线性回归的方程是 y = mx + b，其中 y 是因变量，x 是自变量，m 是直线的斜率，b 是 y 截距。

假设我们有一组 n 个数据点（x1， y1），（x2， y2）， ...，（xn， yn），我们想找到最小化平方误差（SSE）之和的 m 和 b 值：

SSE = Σ（yi — （mx_i + b））²， i = 1 到 n

要使用梯度下降找到 m 和 b 的值，我们需要计算 SSE 相对于 m 和 b 的偏导数：

∂SSE/∂m = Σ-2x_i（yi — （mx_i + b））

∂SSE/∂b = Σ-2（yi — （mx_i + b））

接下来，我们使用梯度下降更新规则更新 m 和 b 的值：

m_new = m — alpha * ∂SSE/∂m

b_new = b — alpha * ∂SSE/∂b

其中阿尔法是学习率。我们重复此过程，直到 m 和 b 的值收敛到最小值。

这是逐步推导：

将 m 和 b 初始化为随机值。
计算SSE相对于m和b的梯度：
∂SSE/∂m = Σ-2x_i（yi — （mx_i + b））
∂SSE/∂b = Σ-2（yi — （mx_i + b））
使用梯度下降更新规则更新 m 和 b：
m_new = m — alpha * ∂SSE/∂m
b_new = b — alpha * ∂SSE/∂b
重复步骤 2 和 3，直到 m 和 b 的值收敛到最小值。

下面是一个使用梯度下降查找 m 和 b 值的 Python 代码示例：

from sklearn.datasets import make_regression
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import cross_val_score
X,y = make_regression(n_samples=100, n_features=1, n_informative=1, n_targets=1,noise=20,random_state=13)
plt.scatter(X,y)

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=2)
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train,y_train)
print(lr.coef_)
print(lr.intercept_)
>>>> [28.12597332]
>>>>-2.271014426178382
y_pred = lr.predict(X_test)
from sklearn.metrics import r2_score
r2_score(y_test,y_pred)
>>>> 0.6345158782661013
class GDRegressor:
    
    def __init__(self,learning_rate,epochs):
        self.m = 100
        self.b = -120
        self.lr = learning_rate
        self.epochs = epochs
        
    def fit(self,X,y):
        # calcualte the b using GD
        for i in range(self.epochs):
            loss_slope_b = -2 * np.sum(y - self.m*X.ravel() - self.b)
            loss_slope_m = -2 * np.sum((y - self.m*X.ravel() - self.b)*X.ravel())
            
            self.b = self.b - (self.lr * loss_slope_b)
            self.m = self.m - (self.lr * loss_slope_m)
        print(self.m,self.b)
        
    def predict(self,X):
        return self.m * X + self.b
    
gd = GDRegressor(0.001,50)
gd.fit(X_train,y_train)
>>>> 28.159367347119066 -2.3004574196824854
y_pred = gd.predict(X_test)
from sklearn.metrics import r2_score
r2_score(y_test,y_pred)
>>>>> 0.6343842836315579

4.5 “收敛和可视化：使用梯度下降找到最佳拟合线”

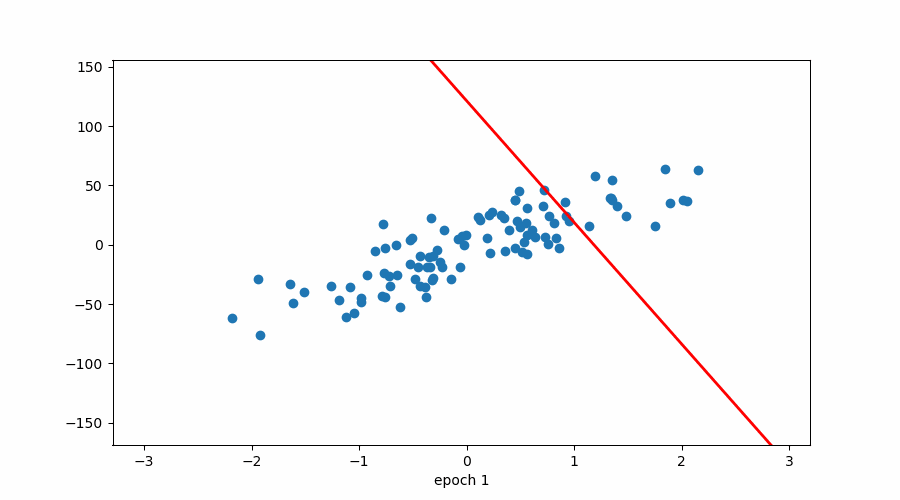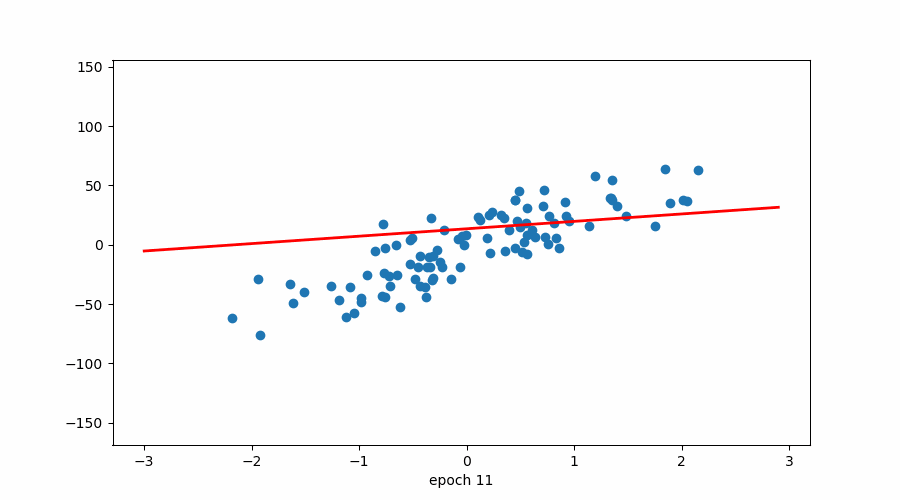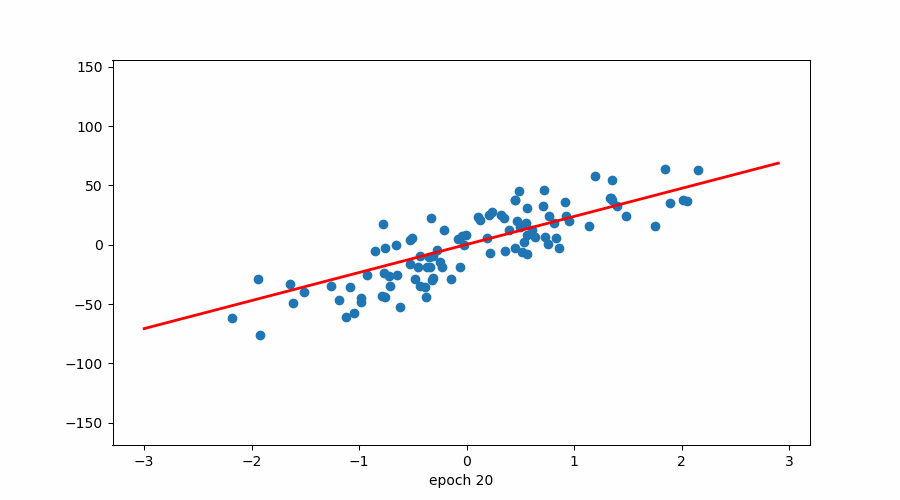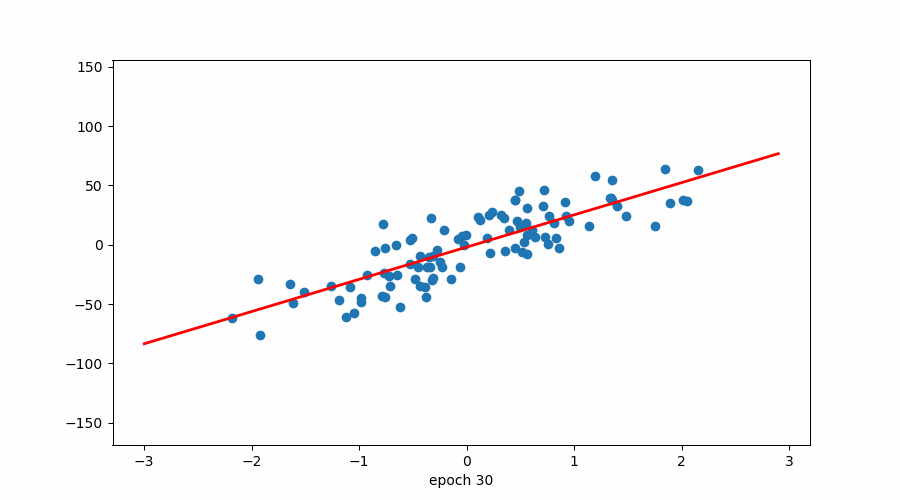
在此可视化中，谷的“暗面”表示损失函数的最小点，其中模型参数经过优化以产生最佳预测。等值线图的形状可以根据模型的复杂性和要优化的参数数量而变化。

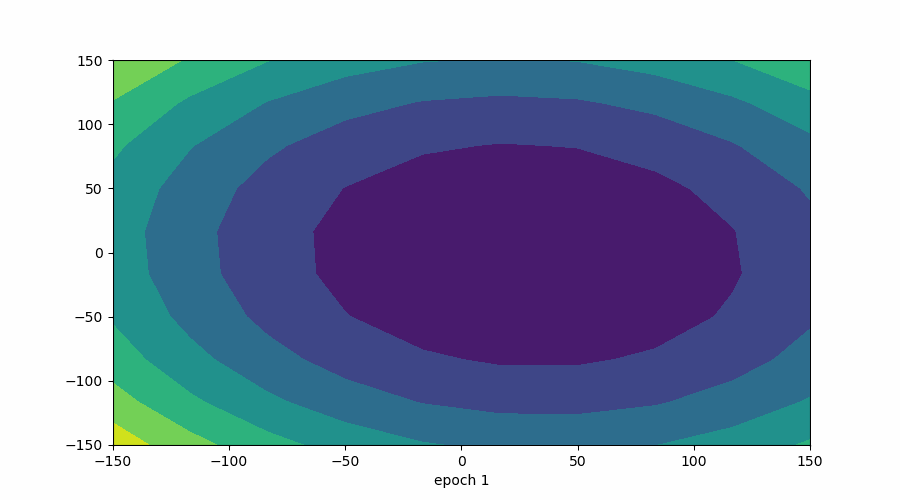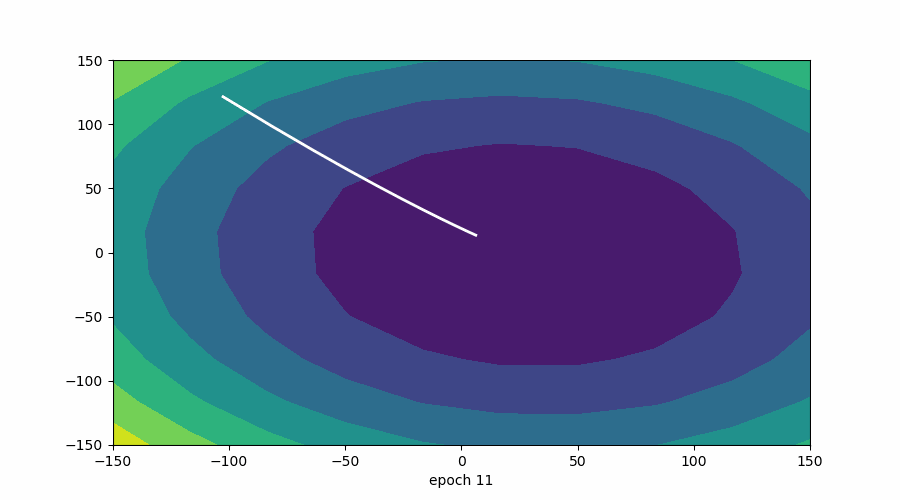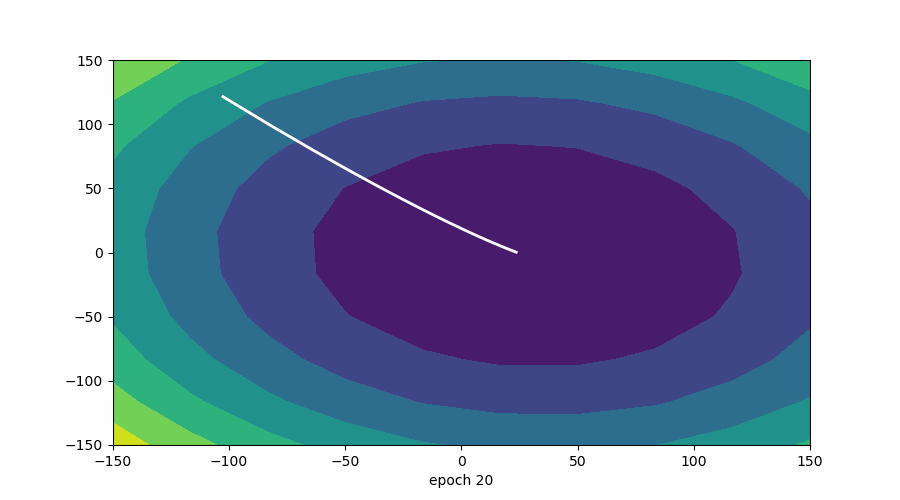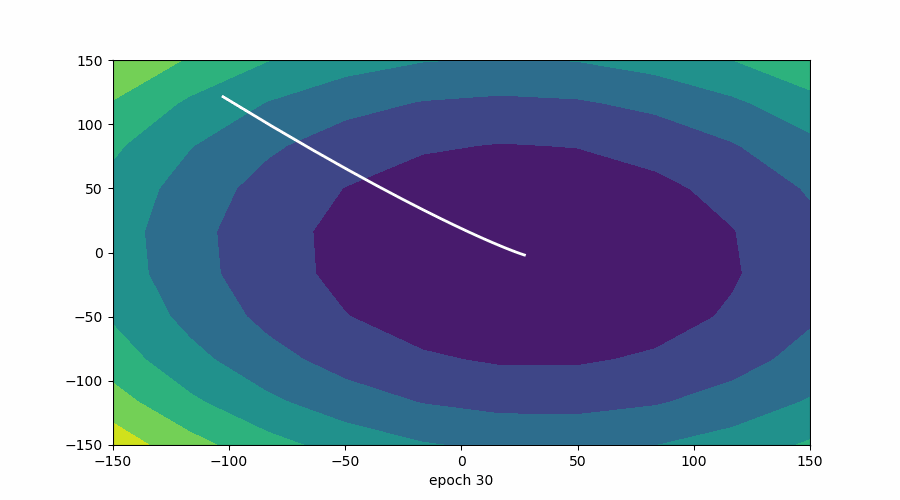
3D 表示

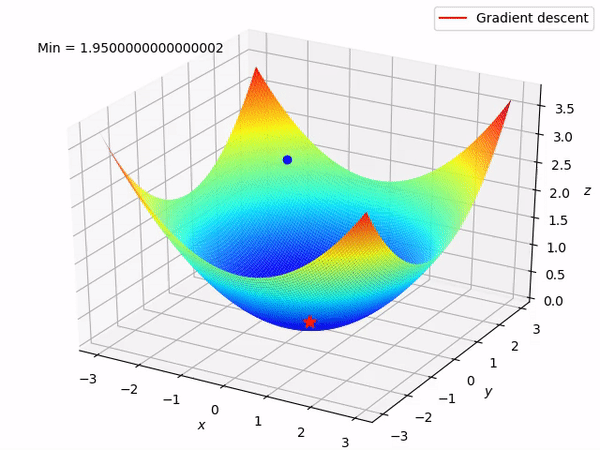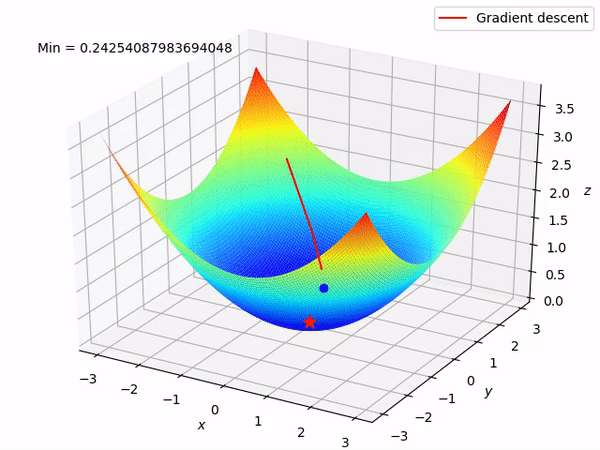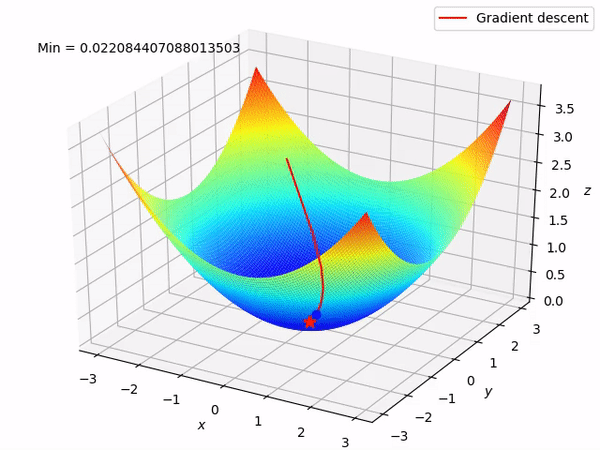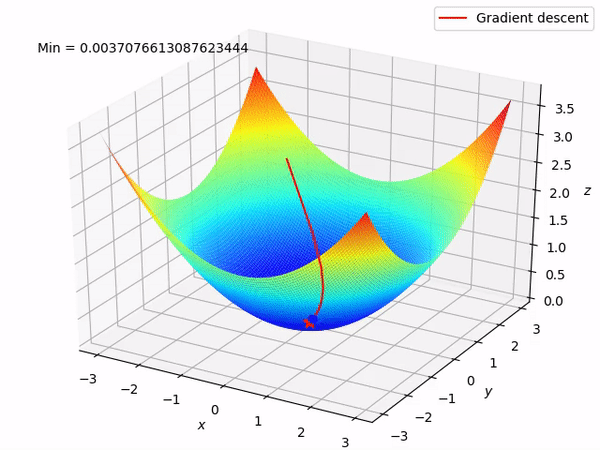
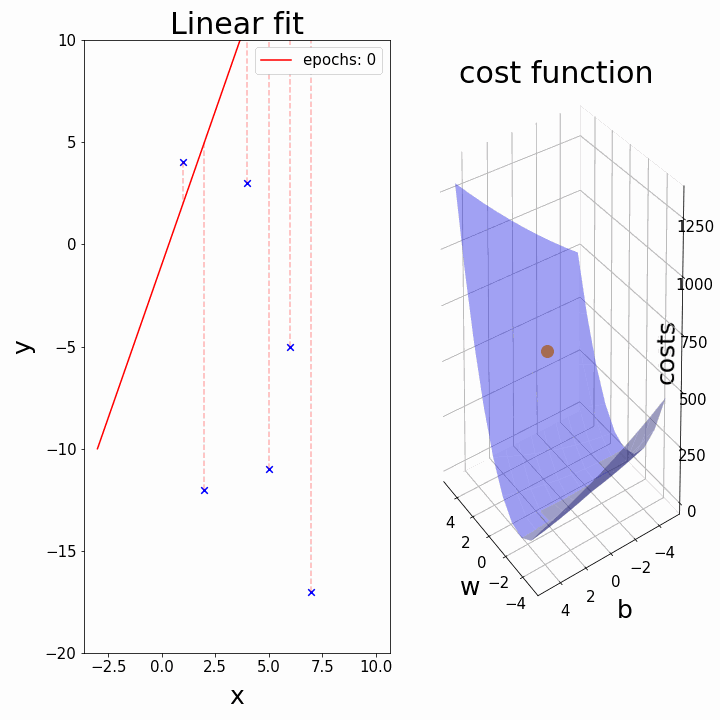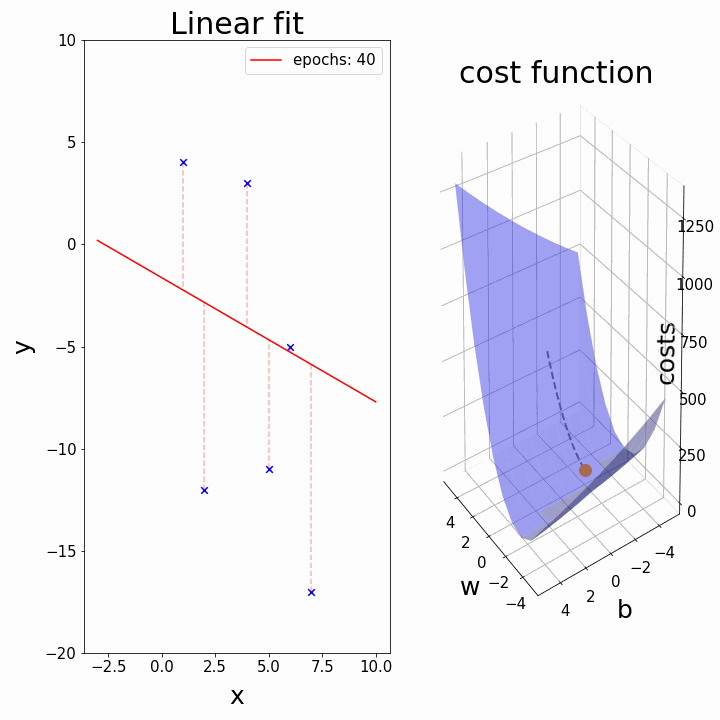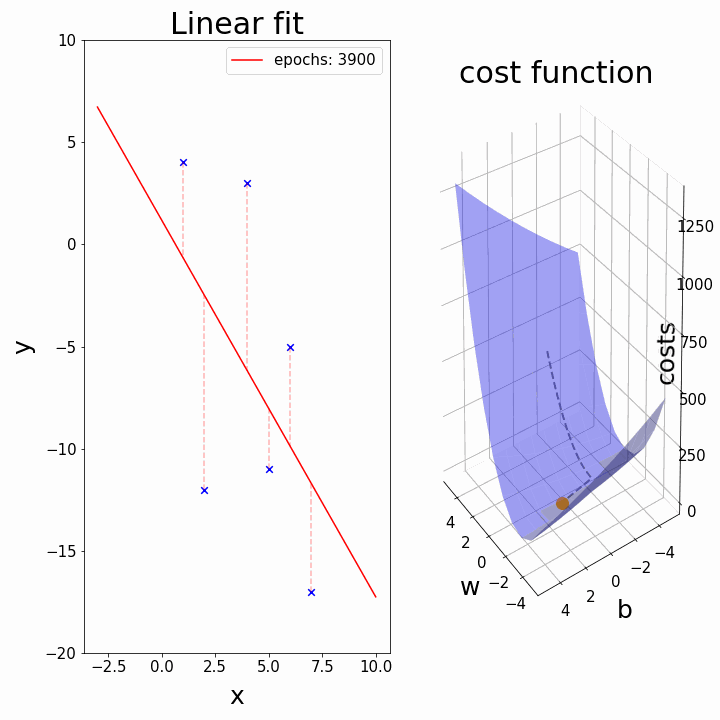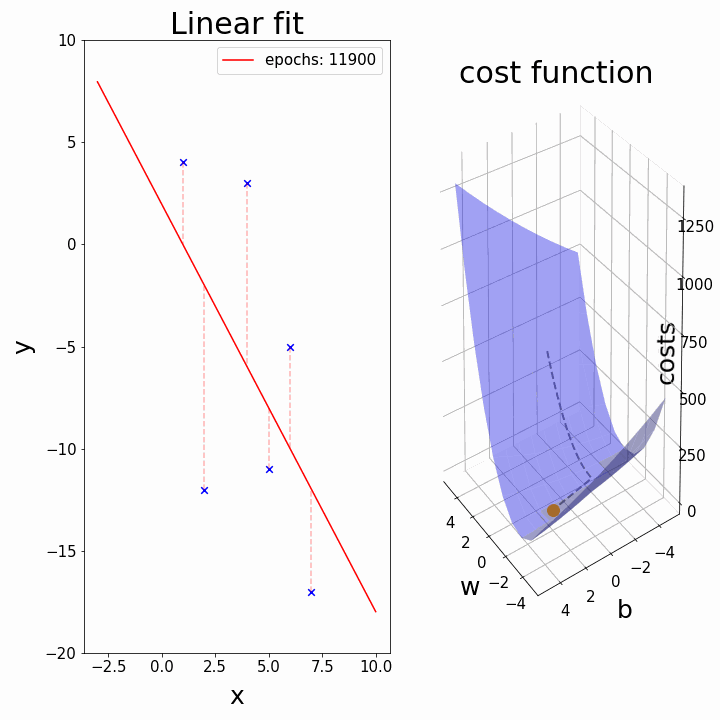
在这里，我们尝试用多元线性回归来表述。

五、多元线性回归模型定义为

y = β0 + β1x1 + β2x2 + ... + βnxn

其中 β0， β1， β2， ...， βn 是我们想要优化的模型的系数（也称为权重或参数）。

5.1 为了找到β0，β1，β2，...，βn的最佳值，我们使用批量梯度下降，它涉及以下步骤：

注意：批量梯度下降与梯度下降上的内容没有什么不同

初始化：我们从系数的一些初始值开始，比如β0 = 0，β1 = 0，β2 = 0，...，βn = 0。
计算成本函数：我们计算成本函数 J（β），用于衡量模型与数据的拟合优度。成本函数通常定义为均方误差（MSE），它是预测值与输出变量 y 的实际值之间的平方差的平均值。
计算梯度：我们计算成本函数相对于系数 β0、β1、β2、...、βn 的梯度。梯度是 n+1 个元素的向量，其中第一个元素对应于 β0，其余元素对应于 β1、β2、...、βn。
更新系数：我们使用梯度下降更新规则更新系数：

βj ：= βj — α * ∂J（β） / ∂βj

其中α是学习率（控制更新大小的超参数），j = 0， 1， 2， ...， n。

重复步骤 2-4 直到收敛：我们重复步骤 2-4，直到成本函数收敛（即停止显着下降）。

5.2 下面是如何将批量梯度下降应用于高维多元线性回归问题的示例：

假设我们有一个数据集，其中包含 n = 10 个特征和 m = 1000 个观测值。目标是根据平方英尺、卧室数量、浴室数量等特征预测房屋价格。

我们可以将数据集表示为 m x （n+1）矩阵 X，其中 X 的第一列是 1 的向量（对于截距项），其余列表示 n 个特征。我们还有一个m元素的向量y，它代表房屋的实际价格。

我们可以将系数 β0， β1， β2， ...， βn 初始化为零，并设置一个学习率α（例如，0.01）。然后，我们可以将成本函数 J（β）计算为：

J（β） = 1/2m * sum（（Xβ — y）²）

其中 Xβ 是基于β系数的当前值预测的房屋价格，并且对所有 m 个观测值求和。

然后，我们可以将成本函数的梯度计算为：

∂J（β） / ∂βj = 1/m * sum（（Xβ — y） * Xj）

其中 Xj 是矩阵 X 的第 j 列，总和被接管

继续 aove

所有 m 观测值。

使用梯度下降更新规则，我们可以将系数更新为：

βj ：= βj — α * ∂J（β） / ∂βj

对于 j = 0， 1， 2， ...， n。此更新规则实质上将系数沿成本函数最陡下降的方向移动，直到达到最小值。

我们可以重复计算成本函数和梯度，以及系数的更新，直到成本函数收敛（即停止显着下降）。一旦系数收敛，我们就有了最适合数据的最优值β0，β1，β2，...，βn。

批量梯度下降的优点是能够收敛到成本函数的全局最小值，但对于大型数据集，它的计算成本可能很高。还有其他优化算法，例如随机梯度下降和小批量梯度下降，对于大型数据集可以更有效。

六、python代码

from sklearn.datasets import load_diabetes
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
X,y = load_diabetes(return_X_y=True)
print(X.shape)
print(y.shape)
>>>> (442, 10)
>>>>> (442,)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=2)
reg = LinearRegression()
reg.fit(X_train,y_train)
LinearRegression()
print(reg.coef_)
print(reg.intercept_)
>>>> [  -9.16088483 -205.46225988  516.68462383  340.62734108 -895.54360867
       561.21453306  153.88478595  126.73431596  861.12139955   52.41982836]
>>>> 151.88334520854633
y_pred = reg.predict(X_test)
r2_score(y_test,y_pred)
>>>>> 0.4399387660024645
X_train.shape
>>>>>> (353, 10)
class GDRegressor:
    
    def __init__(self,learning_rate=0.01,epochs=100):
        
        self.coef_ = None
        self.intercept_ = None
        self.lr = learning_rate
        self.epochs = epochs
        
    def fit(self,X_train,y_train):
        # init your coefs
        self.intercept_ = 0
        self.coef_ = np.ones(X_train.shape[1])
        
        for i in range(self.epochs):
            # update all the coef and the intercept
            y_hat = np.dot(X_train,self.coef_) + self.intercept_
            #print("Shape of y_hat",y_hat.shape)
            intercept_der = -2 * np.mean(y_train - y_hat)
            self.intercept_ = self.intercept_ - (self.lr * intercept_der)
            
            coef_der = -2 * np.dot((y_train - y_hat),X_train)/X_train.shape[0]
            self.coef_ = self.coef_ - (self.lr * coef_der)
        
        print(self.intercept_,self.coef_)
    
    def predict(self,X_test):
        return np.dot(X_test,self.coef_) + self.intercept_
gdr = GDRegressor(epochs=1000,learning_rate=0.5)
gdr.fit(X_train,y_train)
>>>>> 152.0135263267291 [  14.38915082 -173.72674118  491.54504015  323.91983579  -39.32680194
>>>>>  -116.01099114 -194.04229501  103.38216641  451.63385893   97.57119174]
y_pred = gdr.predict(X_test)
r2_score(y_test,y_pred)
>>>>> 0.4534524671450598

梯度下降也称为批量梯度下降。

以下是批量梯度下降（BGD）、随机梯度下降（SGD）和小批量梯度下降（MBGD）收敛性的更详细比较：

BGD：