Java集合类ArrayList的应用-杨辉三角的前n行

news2024/11/30 14:23:27

一、题目

杨辉三角

二、题解

三、代码

四、总结

一、题目

题目链接：https://leetcode.cn/problems/pascals-triangle/description/

杨辉三角

题目描述：给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例一：

输入: numRows = 5

输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例二：

输入: numRows = 1

输出: [[1]]

二、题解

1、在原题目中，一开始给出如下代码：

class Solution {
      public List<List<Integer>> generate(int numRows) {
        
    }

}

可知，让补写的方法的返回类型为 List<List<Integer>> ，我们再看到它的时候，可以想到二维数组是如何存放元素的。我们类比于二维数组，List<List<Integer>>的理解可为外层List集合类容器里面的每一个元素仍是List类。

2、根据返回类型，我们首先可以创建出外层：

List<List<Integer>> ret = new ArrayList<>();
//里面的每一个元素都为ArrayList类型

ret里面的每一个元素就是杨辉三角的其中一行，对于杨辉三角的每一行，我们也用ArrayList类来实现，每一行都创建一个ArrayList顺序表。

如图：

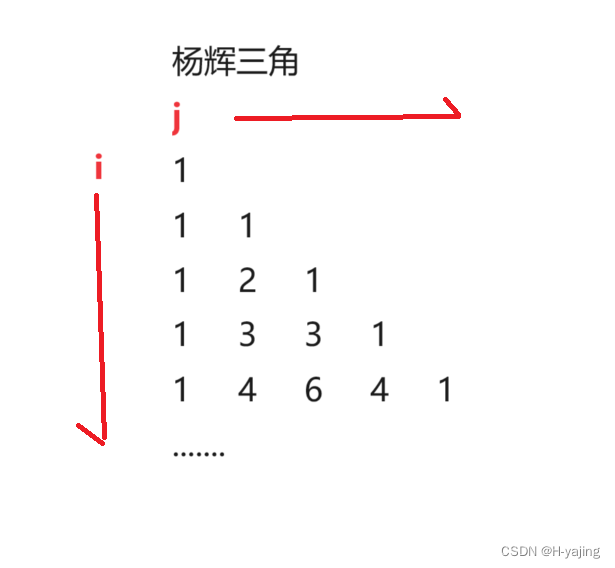
杨辉三角的第一行只有一个元素1，所以第一行我们这样实现：

List<Integer> row1 = new ArrayList<>();
        row1.add(1);
        ret.add(row1);  //将杨辉三角的第一行加入ret

对于第二行至第numRows 行，它们的第一个元素和最后一个元素都是1，而中间元素可以由上一行的两个元素相加，所以如下实现：

for (int i = 1;i < numRows;i++) {
            List<Integer> curRow = new ArrayList<>();
            curRow.add(1);
            List<Integer> prvRow = ret.get(i-1);
            for (int j = 1;j<i;j++) {
               curRow.add(prvRow.get(j)+ prvRow.get(j-1));
            }
            curRow.add(1);
            ret.add(curRow);
        }

三、代码

完整代码如下：

class Solution {
      public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> ret = new ArrayList<>();
        //第一行
        List<Integer> row1 = new ArrayList<>();
        row1.add(1);
        ret.add(row1);
        for (int i = 1;i < numRows;i++) {
            List<Integer> curRow = new ArrayList<>();
            curRow.add(1);
            List<Integer> prvRow = ret.get(i-1);
            for (int j = 1;j<i;j++) {
               curRow.add(prvRow.get(j)+ prvRow.get(j-1));
            }
            curRow.add(1);
            ret.add(curRow);
        }
        return ret;
    }

}