向量空间

向量空间与子空间

当存在这样的一组向量集合$V$，其中$v，u，w$分别为集合$V$中的元素，以及存在标量c，d

1. $u+v\in V$
2. $u+v=v+u$
3. $(u+v)+w=u+(v+w)$
4. $V$中存在一个零向量$0$，使得$0+v=v$
5. 对$V$中每个向量$u$，存在$V$中一个向量$-u$，使得$u+(-u)=0$
6. c$u\in v$
7. c$(u+v)\in V$
8. (c+d)$u\in V$
9. c(d$u$)=(cd)$u$
10. 1$u=u$

若满足上述要求则称$V$为一个向量空间

向量空间$R^n$由所有的$n$维向量$v$组成，向量中的每个元素都是实数。

子空间：一个向量空间的子空间是由一系列包含零向量的向量组成的，并且满足：如果是$w$和$v$是子空间的两个向量并且$c$是任意标量，那么有

1. $c+w$在子空间中
2. $cv$在子空间中。

所以$R^3$ 的子空间可能有

• $L$所有过(0,0,0)的直线
• $P$所有过(0,0,0)的平面
• $Z$只有零向量(0,0,0)
• $R^3$整个空间

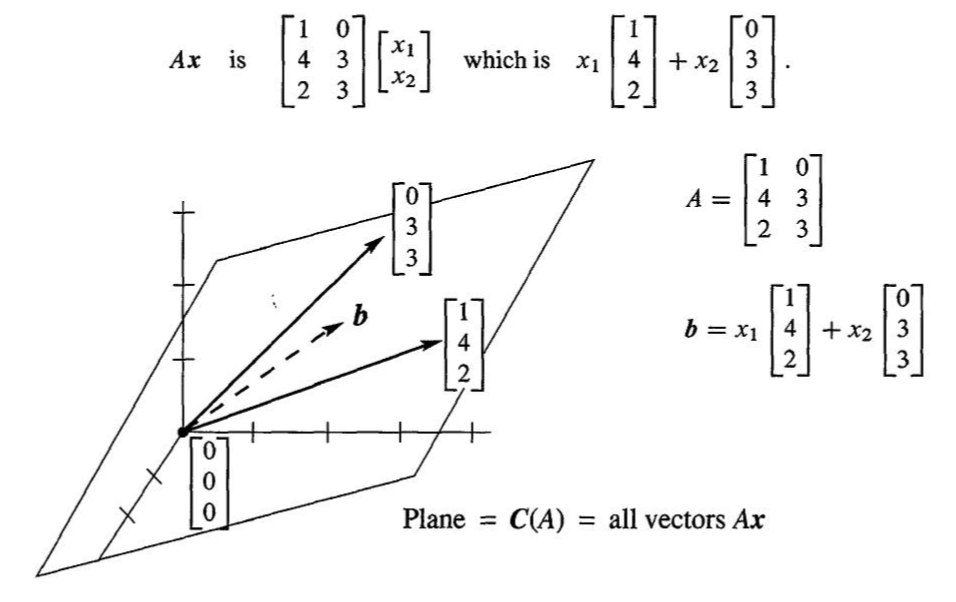
对于$Ax=b$在向量空间上的解释：

$$\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]\cdot \left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]=\left[\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_n\end{array}\right]=x_1\left[\begin{array}{c}{a}_{11}\\ a_{12}\\ ⋮\\ a_{1n}\end{array}\right]+x_2\left[\begin{array}{c}{a}_{21}\\ a_{22}\\ ⋮\\ a_{2n}\end{array}\right]+\cdots x_n\left[\begin{array}{c}{a}_{n1}\\ a_{n2}\\ ⋮\\ a_{nn}\end{array}\right]$$

即将$A$视为一个n维空间的一组向量，而$Ax$可以视为向量空间上向量$A$的线性组合即，若$Ax=b$有解 ，即$b$在该向量空间内，并可以有该向量空间中的一组向量线性表出。

零空间

矩阵$A$的零空间包含所有$Ax=0$的解，这些向量位于$R^n$中，表示为$N(A)$。

假设$x$与$y$在$A$的零空间中，存在$Ax=0$与$Ay=0$，则存在$A(x+y)=0$与$A(cx)=0$，即矩阵$A$的零空间是一个子空间