文章目录
- 647. 回文子串
- 思路
- 暴力解法
- 动态规划五部曲
- 516. 最长回文子序列
- 思路
- 动态规划五部曲
647. 回文子串
力扣题目链接
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = "abc"
输出:3
解释:三个回文子串: "a", "b", "c"
示例 2:
输入:s = "aaa"
输出:6
解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
思路
注意这道题要求的子串是要由连续的字符组成
暴力解法
两层for循环,一个遍历子串起始位置,一个遍历终止位置,找出所有可能的子串,然后判断是不是回文的。
动态规划五部曲
- 确定dp数组以及下标的含义
dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
- 确定递推公式
分为两种情况讨论:
- 当
s[i]与s[j]不相等
头尾两个字符不相等,那肯定的不是回文串,此时dp[i][j] = false
- 当
s[i]与s[j]相等时- 情况一:下标
i与j相同,即同一个字符,例如a,必然是回文子串,此时dp[i][j] = true - 情况二:下标
i与j相差为1,即字符串由两个相同的字符组成,例如aa,必然是回文子串,此时dp[i][j] = true - 情况三:下标
i与j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,再看aba是不是回文就可以了,那么aba的区间就是i+1与j-1区间,即判断dp[i + 1][j - 1]是否为true。
- 情况一:下标
if (s.charAt(i) == s.charAt(j)) {
if (j - i <= 1) {
res++;
dp[i][j] = true;
}else if (dp[i + 1][j - 1] == true) {
res++;
dp[i][j] = true;
}
}
result就是统计回文子串的数量。
注:这里我没有列出当s[i]与s[j]不相等的时候,因为在下面dp[i][j]初始化的时候,就初始为false。
- dp数组如何初始化
dp[i][j]刚开始是不知道是否回文的,所以dp[i][j]都初始化为false。
- 确定遍历顺序
首先从递推公式中可以看出,情况三是根据**dp[i + 1][j - 1]**是否为true,再对dp[i][j]进行赋值的。
这两个式子的相对位置如下:
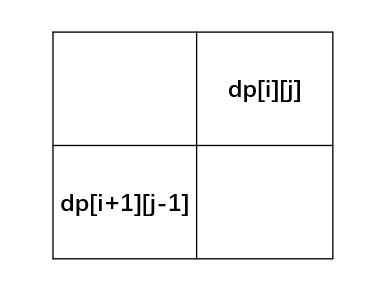
发现dp[i + 1][j - 1] 在 dp[i][j]的左下角
所以一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。这样计算i的时候才能预先得到i+1的值。
// 记住从下往上,从左往右
for (int i = s.length() - 1; i >= 0; i--) {
for (int j = i; j < s.length(); j++) {
- 举例推导dp数组
用示例二举例,输入:“aaa”,dp[i][j]状态如下:
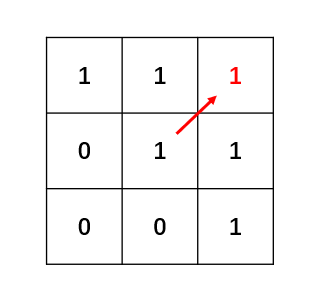
图中有6个true,所以就是有6个回文子串。
注:因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分。
完整代码:
public int countSubstrings(String s) {
boolean[][] dp = new boolean[s.length()][s.length()];
int res = 0; // 记录回文子串总数
// 记住从下往上,从左往右
for (int i = s.length() - 1; i >= 0; i--) {
for (int j = i; j < s.length(); j++) {
if (s.charAt(i) == s.charAt(j)) {
if (j - i <= 1) {
res++;
dp[i][j] = true;
}else if (dp[i + 1][j - 1] == true) {
res++;
dp[i][j] = true;
}
}
}
}
return res;
}
516. 最长回文子序列
力扣题目链接
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例 1:
输入:s = "bbbab"
输出:4
解释:一个可能的最长回文子序列为 "bbbb" 。
示例 2:
输入:s = "cbbd"
输出:2
解释:一个可能的最长回文子序列为 "bb" 。
思路
注意这里的子序列只用满足相对顺序,不用连续
动态规划五部曲
- 确定dp数组以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
- 确定递推公式
和上一题一样,同样是两个情况
-
如果
s[i]与s[j]不相同,说明s[i]和s[j]的同时加入并不能增加[i,j]区间回文子串的长度,那我们就考虑是留下果s[i]还是s[j]继续找回文子串-
留下
s[i],去掉s[j]找回文子序列,此时dp[i][j] = dp[i][j - 1]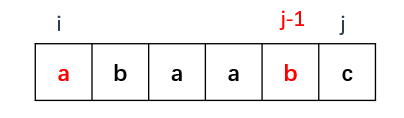
-
留下
s[j],去掉s[i]找回文子序列,此时dp[i][j] = dp[i + 1][j]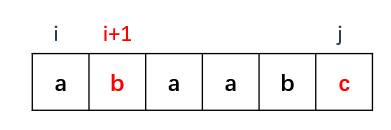
-
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
-
如果
s[i]与s[j]相同 -
- 如果
i == j,即字符串长度为1,一定是回文子串,dp[i][j] = 1; - 如果
j - i == 1,即字符串由两个相同的字符组成,一定是回文子串,dp[i][j] = 2; - 如果
j - i >1,这时候我们要看里面子串的最长回文子序列长度,如果里面也是回文,那么就最后要加上s[i]与s[j]这两个字符,如下图,所以dp[i][j] = dp[i+1][j-1] + 2;
- 如果
if (s.charAt(i) == s.charAt(j)) {
if (j - i <= 1) { // 情况一二
dp[i][j] = j - i + 1;
}else { // 情况三
dp[i][j] = dp[i + 1][j - 1] + 2;
}
} else { // s[i]和s[j]不等
dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
}
- dp数组如何初始化
一开始不知道范围内存不存在回文子序列,所以全部初始化为0
- 从递推公式
dp[i][j] = dp[i + 1][j - 1] + 2和dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])可以看出,dp[i][j]是依赖于dp[i + 1][j - 1]和dp[i + 1][j]
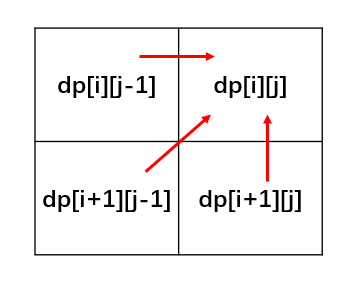
所以遍历i的时候一定要从下到上,从左到右遍历,这样才能保证,下一行的数据是经过计算的。
for (int i = s.length() - 1; i >= 0; i--) {
for (int j = i; j < s.length(); j++) {
- 举例推导dp数组
以示例二为例,输入s:“cbbd” 为例,dp数组状态如图:
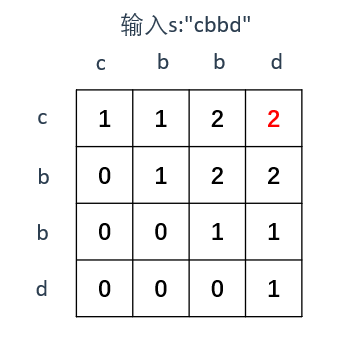
完整代码:
public int longestPalindromeSubseq(String s) {
int[][] dp = new int[s.length()][s.length()];
for (int i = s.length() - 1; i >= 0; i--) {
for (int j = i; j < s.length(); j++) {
if (s.charAt(i) == s.charAt(j)) {
if (j - i <= 1) { // 情况一二
dp[i][j] = j - i + 1;
}else { // 情况三
dp[i][j] = dp[i + 1][j - 1] + 2;
}
} else { // s[i]和s[j]不等
dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
}
}
}
return dp[0][s.length() - 1];
}