一、题设

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

二、基本思路

        动态规划题，首先明确一下动规的基本五部曲：

        step1: 明确动态数组dp以及下标的含义:dp[i]表示到第i层楼梯有几种爬法.

        step2:确定动态转移方程:也就是dp[i]是怎么来的，题目说可以一次爬一个台阶和两个台阶，那么状态转移方程就很明显了：dp[i] = dp[i-1] + dp[i-2] （dp[i-1]表示这次爬了一个台阶，dp[i-2]表示这次爬了两个台阶）.

        step3:初始化：因为转移方程涉及到 i-1 和 i-2 ，那么我们赋值前两个就可以了：dp[1] = 1,dp[2] = 2.

        step4:遍历顺序，一维数组遍历即可。（从 i = 2开始）.

        step5:打印dp看一下与实际含义是否一致：一致.

三、代码实现

    def climbStairs(self, n):
        dp = [0 for _ in range(n+1)]
        # 两个特殊情况处理一下
        if n==1:
            return 1
        if n== 2:
            return 2
        dp[1],dp[2] = 1,2
        for i in range(3,n+1):
            # i - 1：这次爬一个台阶
            # i - 2：这次爬两个台阶
            dp[i] = dp[i-1] + dp[i-2]
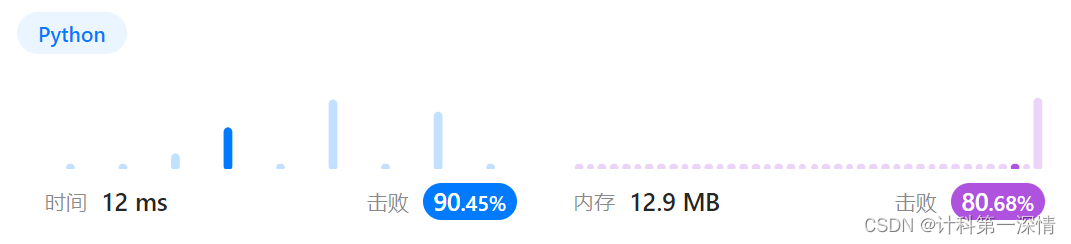
        return dp[-1]

四、效率总结