目录
LeetCode之路——232. 用栈实现队列
分析:
LeetCode之路——225. 用队列实现栈
分析:

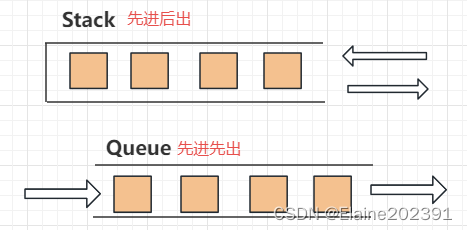
栈(Stack)和队列(Queue)是两种基本的数据结构,它们在计算机科学中用于不同的目的。以下是它们的定义和主要特点:
栈 (Stack):
-
栈是一种线性数据结构,具有后进先出(Last-In, First-Out,LIFO)的特性,即最后入栈的元素最先出栈。
-
栈通常支持两个主要操作:
push(入栈)和pop(出栈)。push操作将元素添加到栈的顶部,而pop操作从栈的顶部移除元素。 -
除了
push和pop,栈还支持peek操作,用于查看栈顶的元素而不移除它。 -
栈的应用包括函数调用的调用栈、表达式求值(后缀表达式)、浏览器历史记录等。
队列 (Queue):
-
队列是一种线性数据结构,具有先进先出(First-In, First-Out,FIFO)的特性,即最早入队的元素最早出队。
-
队列支持两个主要操作:
enqueue(入队)和dequeue(出队)。enqueue操作将元素添加到队列的尾部,而dequeue操作从队列的头部移除元素。 -
除了
enqueue和dequeue,队列还支持peek操作,用于查看队列头部的元素而不移除它。 -
队列的应用包括任务调度、广度优先搜索算法、打印队列、消息传递系统等。
总结:
栈和队列都是重要的数据结构,它们在不同的应用场景中都发挥着重要作用。栈适用于需要后进先出顺序的问题,而队列适用于需要先进先出顺序的问题。选择合适的数据结构取决于问题的性质和需求。
LeetCode之路——232. 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
-
void push(int x)将元素 x 推到队列的末尾 -
int pop()从队列的开头移除并返回元素 -
int peek()返回队列开头的元素 -
boolean empty()如果队列为空,返回true;否则,返回false
说明:
-
你 只能 使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。 -
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
示例 1:
输入: ["MyQueue", "push", "push", "peek", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 1, 1, false] 解释: MyQueue myQueue = new MyQueue(); myQueue.push(1); // queue is: [1] myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue) myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2] myQueue.empty(); // return false
分析:
适合用来理解栈和队列。
public class MyQueue {
Stack<Integer> input;
Stack<Integer> output;
public MyQueue() {
input = new Stack<>();
output = new Stack<>();
}
public void push(int x) {
input.push(x);
}
public int pop() {
dumpInput();
return output.pop();
}
public int peek() {
dumpInput();
return output.peek();
}
public boolean empty() {
return input.isEmpty() && output.isEmpty();
}
public void dumpInput() {
if (!output.isEmpty()) return;
while (!input.isEmpty()) {
output.push(input.pop());
}
}
}
-
时间复杂度:O(1)
-
空间复杂度:O(n)
LeetCode之路——225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
-
void push(int x)将元素 x 压入栈顶。 -
int pop()移除并返回栈顶元素。 -
int top()返回栈顶元素。 -
boolean empty()如果栈是空的,返回true;否则,返回false。
注意:
-
你只能使用队列的基本操作 —— 也就是
push to back、peek/pop from front、size和is empty这些操作。 -
你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入: ["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 2, 2, false] 解释: MyStack myStack = new MyStack(); myStack.push(1); myStack.push(2); myStack.top(); // 返回 2 myStack.pop(); // 返回 2 myStack.empty(); // 返回 False
分析:
队列是先进先出的规则,把一个队列中的数据导入另一个队列中,数据的顺序并没有变,并没有变成先进后出的顺序。
用两个队列模拟栈,其中一个队列是用来备份的。备份队列的目的就是把主队列最后的元素以外元素进行备份。
public class MyStack {
Queue<Integer> mainQ;
Queue<Integer> backQ;
public MyStack() {
mainQ = new LinkedList<>();
backQ = new LinkedList<>();
}
public void push(int x) {
// 先放在backQ中
backQ.offer(x);
while (!mainQ.isEmpty()) {
backQ.offer(mainQ.poll());
}
Queue<Integer> temp = new LinkedList<>();
temp = mainQ;
mainQ = backQ;
backQ = temp; // 交换两个队列,将元素都放到了mainQ中
}
public int pop() {
return mainQ.poll();
}
public int top() {
return mainQ.peek();
}
public boolean empty() {
return mainQ.isEmpty();
}
}
-
时间复杂度:入栈是O(n),其余是O(1)
-
空间复杂度:O(n)