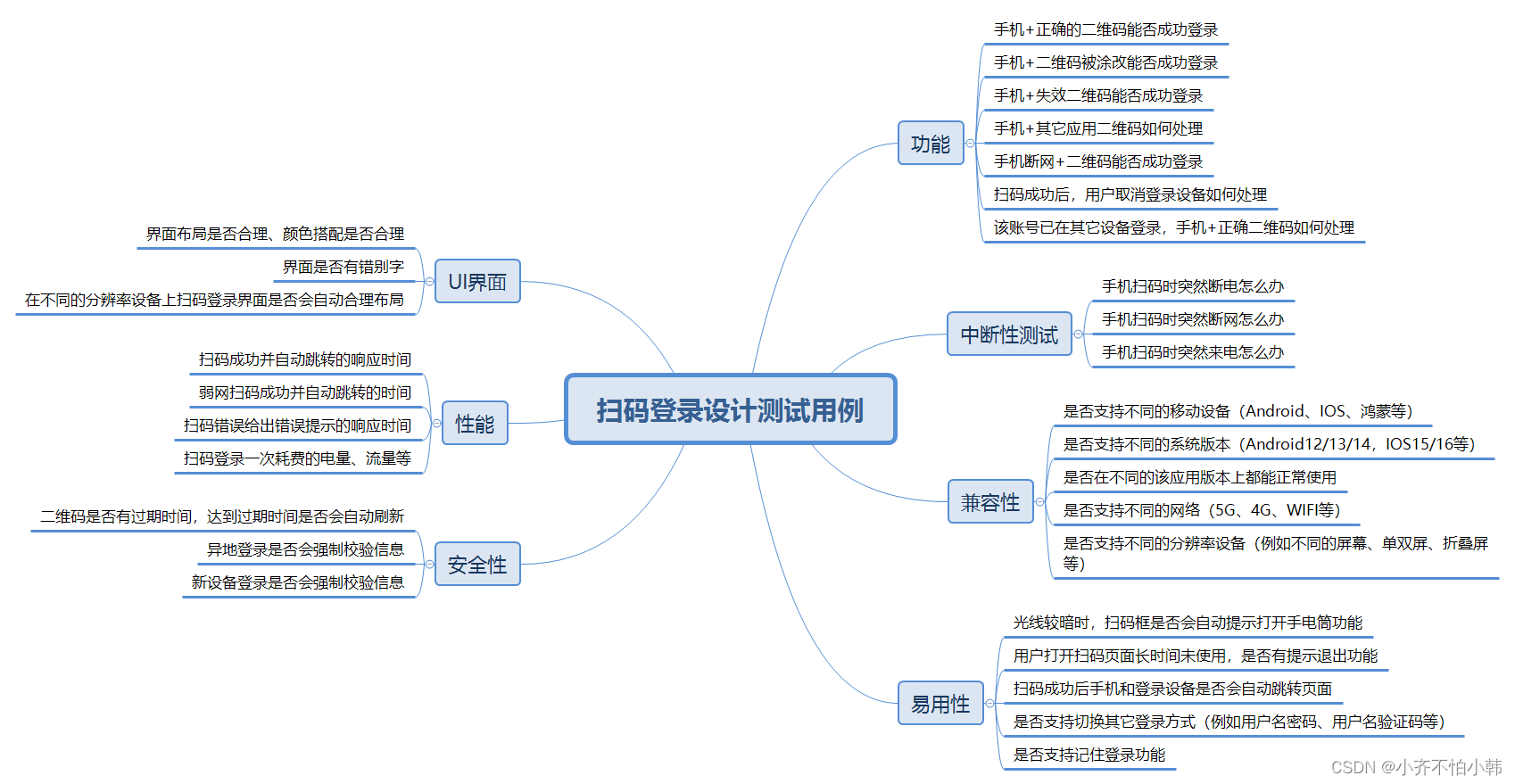
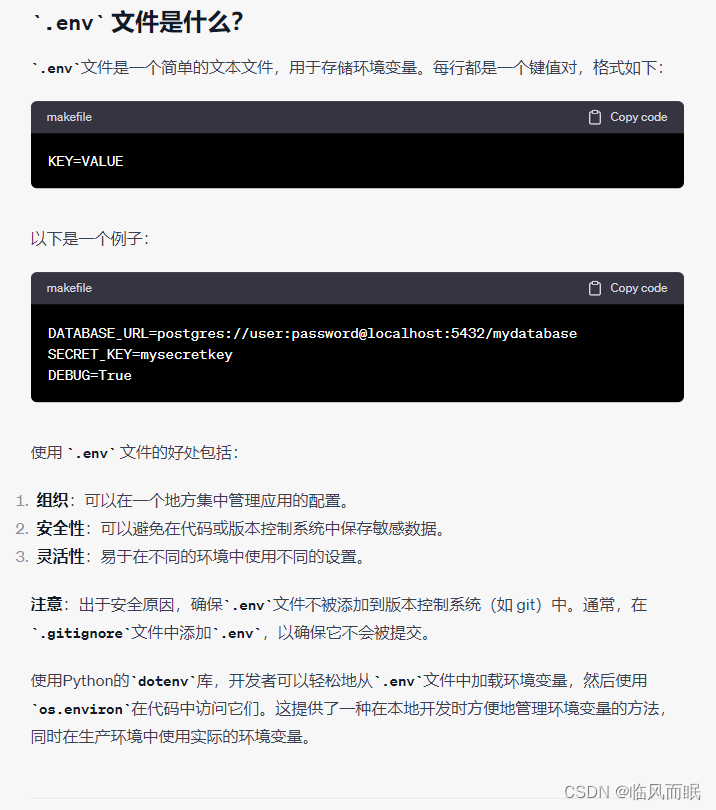
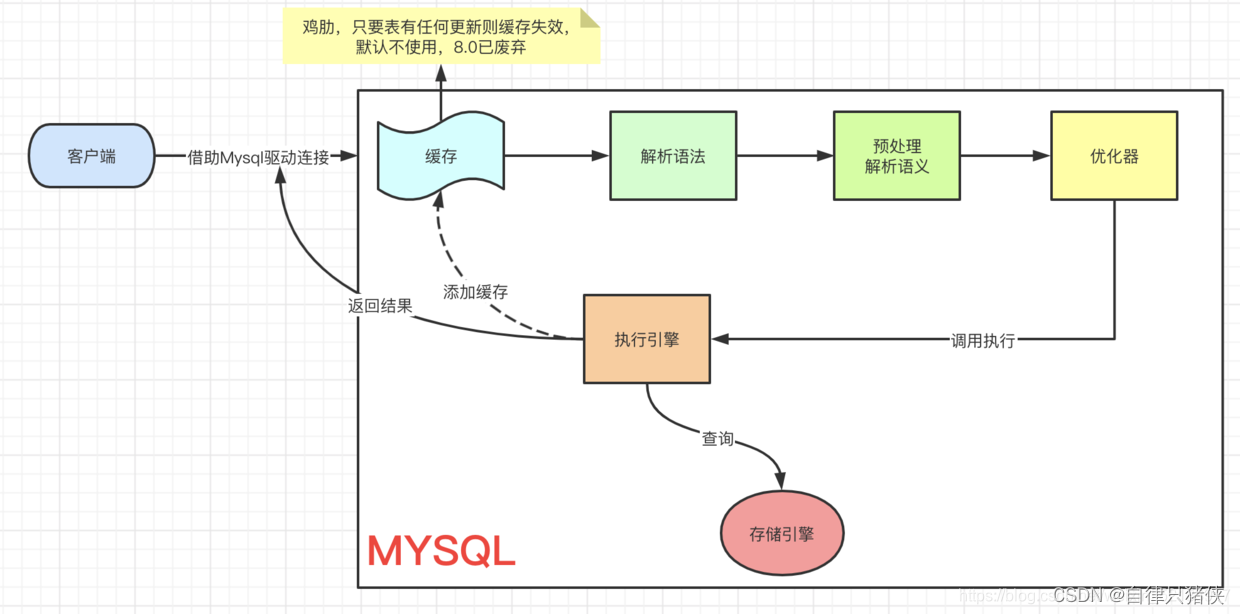
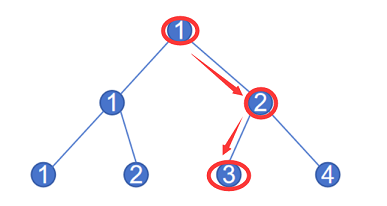
1.1线性模型
线性模型(linear models)是一类最简单的有监督机器学习模型,常被用于简单的机
器学习任务。可以将线性模型视为单层的神经网络。本节讨论线性回归、逻辑斯蒂回归(logistic regression)、 softmax 分类器等三种模型。
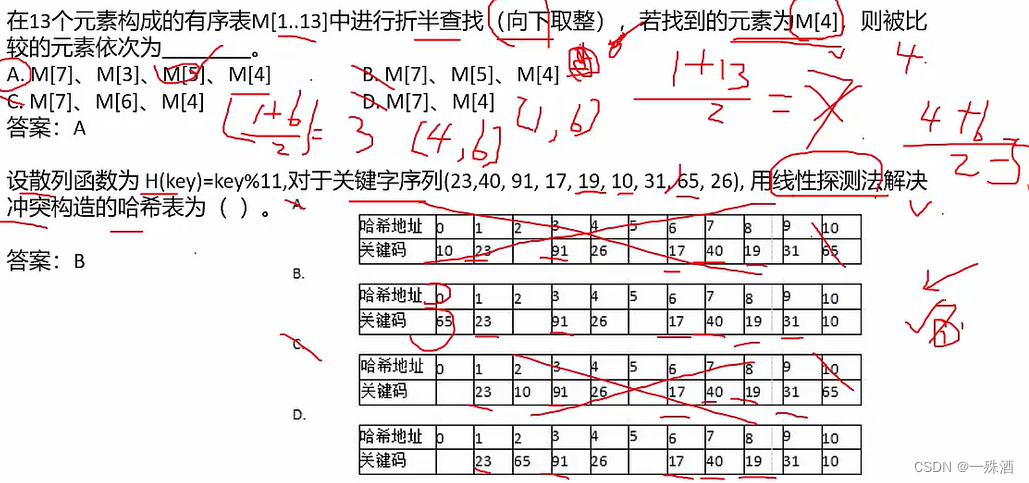
1.1.1线性回归
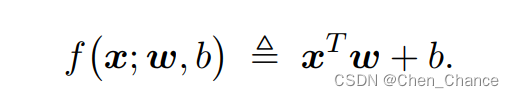
1.1.2逻辑斯蒂回归
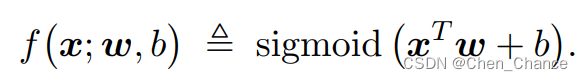
sigmoid 是个激活函数(activation function)
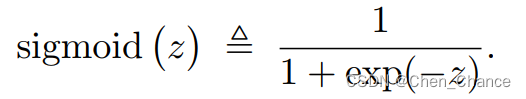
交叉熵(cross entropy),它常被用作分类问题的损失函数
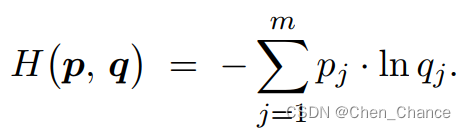
与交叉熵类似的是 KL 散度(Kullback-Leibler divergence),也被称作相对熵(relative entropy),用来衡量两个概率分布的区别有多大。对于离散分布, KL 散度的定义为
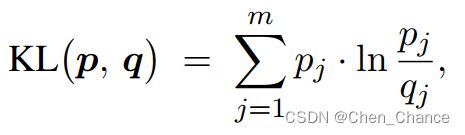
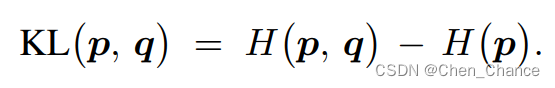
由于熵
H
(
p
)
H(p)
H(p) 是不依赖于 q 的常数,一旦固定 p,则 KL 散度等于交叉熵加上常数。如果p 是固定的,那么关于 q 优化 KL 散度等价于优化交叉熵。这就是为什么常用交叉熵作为损失函数。

1.1.3 Softmax 分类器
本小节研究多元分类(multi-class classification)问题,数据可以划分为 k(> 2)个类别。

softmax 函数让最大的元素相对变得更大,让小的元素接近 0。
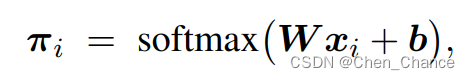
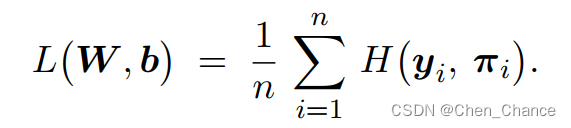
1.2神经网络
本节简要介绍全连接神经网络和卷积神经网络,并将它们用于多元分类问题。全连接层和卷积层被广泛用于深度强化学习。循环层和注意力层也是常见的神经网络结构,本书将在需要用到它们的地方详细讲解这两种结构。
1.2.1 全连接神经网络(多层感知器)
线性分类器表现差的原因在于模型太小,不能充分利用n = 60, 000 个训练样本。然而我们可以把“线性函数 + 激活函数”这样的结构一层层堆积起来,得到一个多层网络,获得更高的预测准确率。
全连接层:
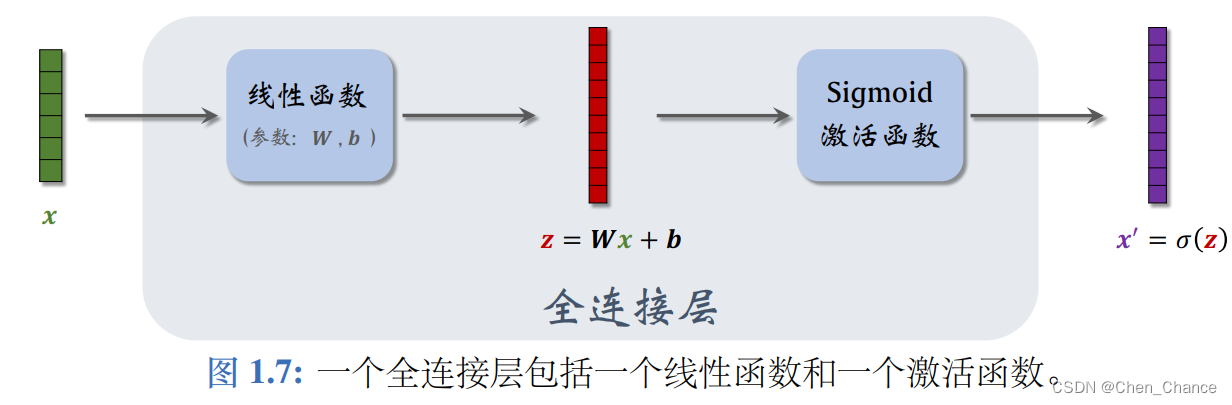
全连接神经网络
我们可以把全连接层当做基本组件,然后像搭积木一样搭建一个全连接神经网络(fully-connected neural network),也叫多层感知器(multi-layer perceptron,缩写 MLP)
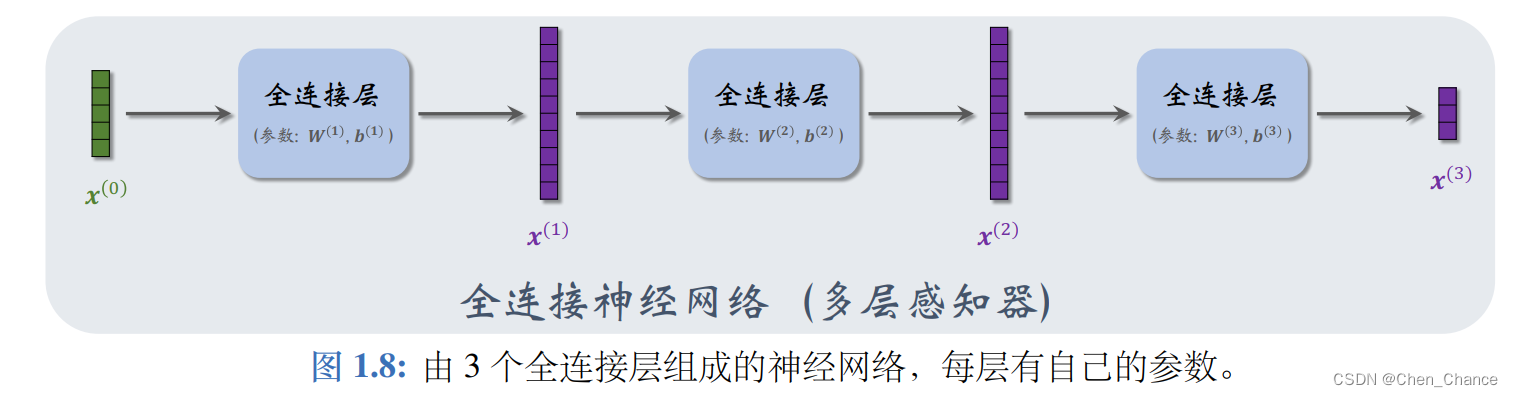
编程实现:
可以用 TensorFlow、 PyTorch、 Keras 等深度学习标准库实现全连接神经网络,只需要一、两行代码就能添加一个全连接层。添加一个全连接层需要用户指定两个超参数:
- 层的宽度
比如 MNIST数据集有 10 类,那么输出层的宽度必须是 10。而对于二元分类问题,输出层的宽度是 1。 - 激活函数
对于隐层,通常使用 ReLU 激活函数。对于输出层,激活函数的选择取决于具体问题。二元分类问题用 sigmoid,多元分类问题用 softmax,回归问题可以不用激活函数。
1.2.2 卷积神经网络
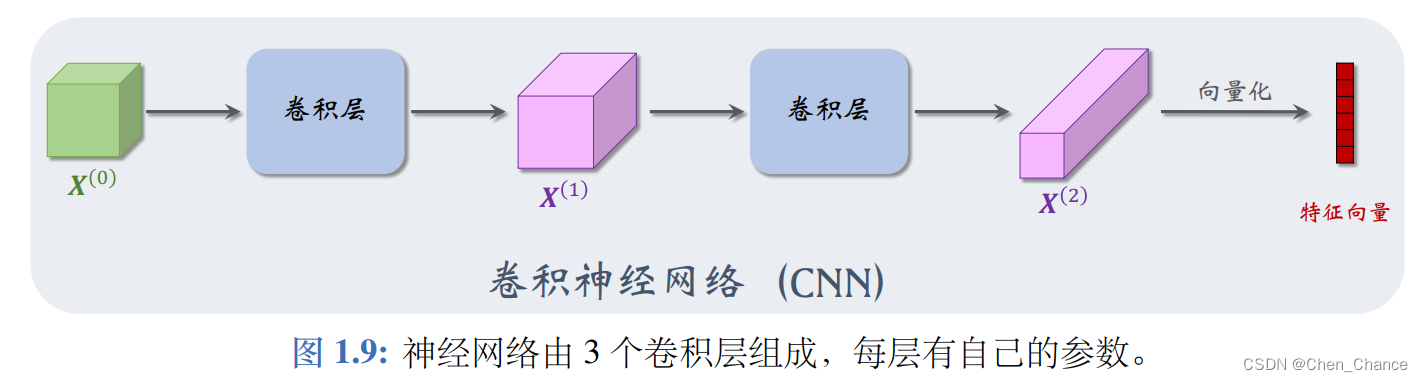
卷积神经网络(convolutional neural network,缩写 CNN)是主要由卷积层组成的神经网络.
把最后一个卷积层输出的张量转换为一个向量,即向量化(vectorization)。这个向量是 CNN 从输入的张量中提取的特征。
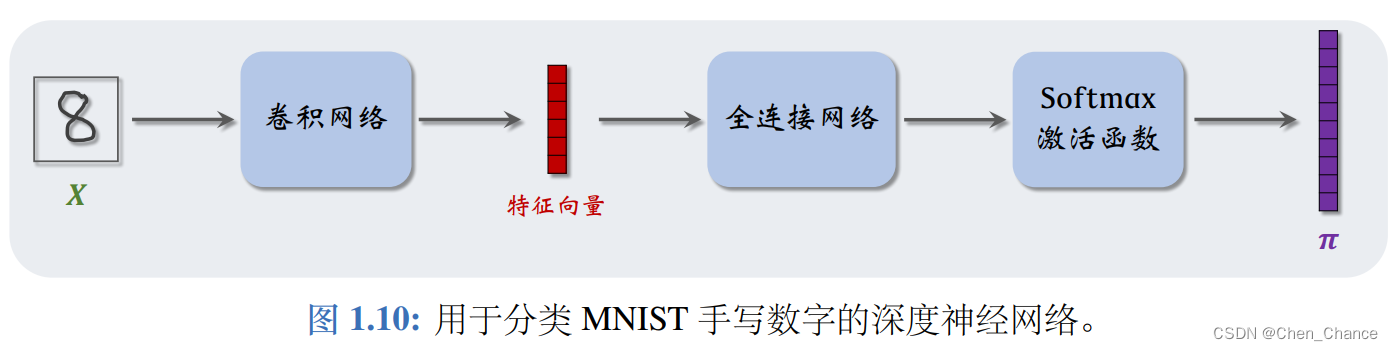
本书不具体解释 CNN 的原理,本书也不会用到这些原理。读者仅需要记住这个知识点: CNN 的输入是矩阵或三阶张量, CNN 从该张量中提取特征,输出提取的特征向量。
图片通常是矩阵(灰度图片)和三阶张量(彩色图片),可以用 CNN 从中提取特征,然后用一个或多个全连接层做分类或回归。
1.3反向传播和梯度下降

对于这样一个无约束的最小化问题,最常使用的算法是梯度下降(gradient descent, 缩写GD)和随机梯度下降(stochastic gradient descent, 缩写 SGD)。
1.3.1 梯度下降
1.3.2 反向传播
SGD 需要用到损失函数关于模型参数的梯度。对于一个深度神经网络,我们利用反
向传播(backpropagation, 缩写 BP)求损失函数关于参数的梯度。如果用TensorFlow 和PyTorch 等深度学习平台,我们可以不关心梯度是如何求出来的。只要定义的函数关于某个变量可微, TensorFlow 和 PyTorch 就可以自动求该函数关于这个变量的梯度。