leetCode 72. 编辑距离动态规划 + 滚动数组 + 优化空间

news2025/2/1 17:03:09

72. 编辑距离 - 力扣（LeetCode）

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

编辑距离的应用场景：DNA的编辑，大段大段的DNA，找到几个关键的节点，做插入做替换，可能就能得到目标DNA了

>>思考和分析：

首先，对这个问题做一个定义，然后把这个问题进行分解。怎么分解呢？考虑它的最后一步，此题我们就考虑S1和S2的末尾字符是否相同，相同的话，我该怎么处理？不相同的话，插入删除替换这三种操作又会进入到什么问题思考？

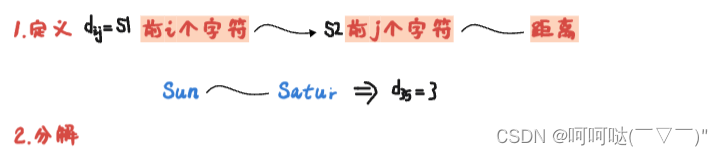
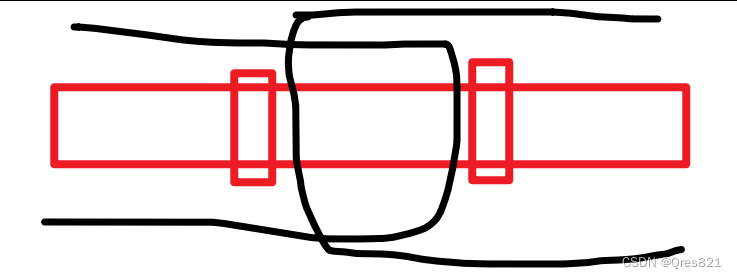
1.S1和S2的末尾字符相同，意味着可以剥离出去相同的，如图蓝色的线表示将x剥离出去。那么剩下要考虑的是S1的前i-1个字符如何编辑才能得到S2的前j-1个字符的问题(O_O)?

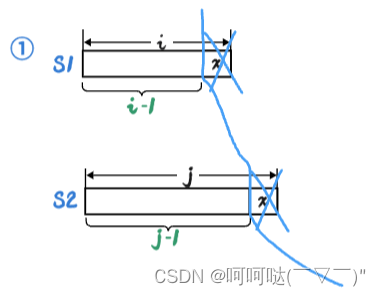
if(S1[i-1] == S2[j-1])
        dp[i][j] = dp[i-1][j-1];

2.S1和S2的末尾字符是不相同的，到底是插入，是删除，还是替换？

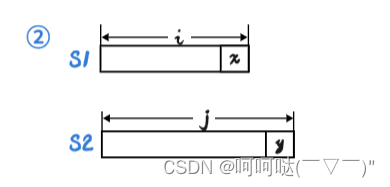
问题思考(O_O)?：如果我要进行插入操作，我是对谁进行操作？

其实是对S1操作，也只能对S1进行操作，也就是我认为S2的末尾是y，S1的末尾不是y，选择把y给插到S1的末尾。因为可能 S1的这 i 个字符 跟 S2的 j-1 个字符其实是具有高度的相似性的，就是S1末尾缺了一个y。所以我选择插入

dp[i][j] = dp[i][j-1]+1;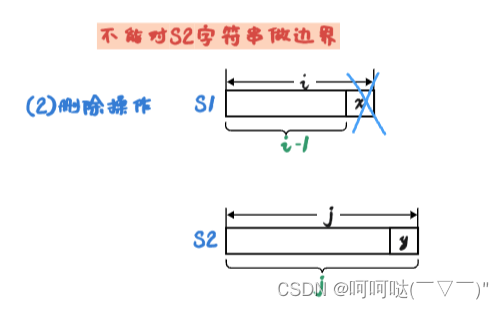

若执行删除操作，也只能对S1操作，我把S1的末尾给删掉，意味着 S1的前i-1个字符和 S2的前j个字符是具有高度的相似性的。就是仅仅因为S1的末尾多了个x，所以我把x删掉

dp[i][j] = dp[i-1][j]+1;

若执行替换操作，可能出现的场景。那可能是认为 S1的前i-1个字符 和 S2的前j-1个字符具有高度的相似性，仅仅是S1的末尾字符是x，S2的末尾字符是y，只要把这个x换成y，就可以达到最优解！（一定要强调是对S1进行的操作）

dp[i][j] = dp[i-1][j-1]+1;

综上，可以得出这样的递推式：

if(S1[i-1] == S2[j-1])
    dp[i][j] = dp[i-1][j-1];
else
    dp[i][j] = min(dp[i][j-1]+1,dp[i-1][j]+1,dp[i-1][j-1]+1);

问题思考(O_O)?：我到底是进行插入、删除还是替换操作呢？比如说背包问题，我这件物品到底是放还是不放呢？其实对于算法而言，它当时并不知道，只知道按照这个方式进行分解就可以了，总之就是这么两种方式分解，没有什么别的选择方案！对于此题也是一样，要么插入、要么删除、要么替换，在这三种方案里面选一个，编辑距离选一个代价最小的，就可以了！

从上图的左边表格，我们可以看到最终结果为3，也就是最少编辑次数为3。仔细看图中我做的标记，字符串S1="sun" 和 S2="satur"，一开始都有相同的 's'，所以不做编辑操作，接着执行两次插入操作。有相同的 'u'，所以不用做编辑操作。最后将 n 替换成 r。可以模拟实现下图的操作效果：

伪代码：

int edit_ distance(S1,m,S2,n) {
    d[][] = {0};
    for(i=1;i<=m;i++) dp[i][0] = i;
    for(j=1;j<=n;j++) dp[0][j] = j;
    for(i=1;i<=m;i++)
        for(j=1;j<=n;j++)
            if(S1[i-1] == S2[j-1]) dp[i][j] = dp[i-1][j-1];
            else dp[i][j] = 1 + min(dp[i][j-1],
                                    dp[i-1][j],
                                    dp[i-1][j-1]);
    return dp[m][n];
}
// 时间复杂度:O(m*n)

问题思考(O_O)?：有些场景应用里，会要求插入、删除、替换的编辑代价是不一样的，那现实生活中也确实会出现这样的情况，比如插入方便一点，替换麻烦一点，那个时候我们代码如何改呢？只要把这个1改一下，不要写1，把编辑代价加到对应的操作上即可！

（1）二维dp

dp[i][j]：S1的前i个字符转换成 S2的前j个字符所使用的最少操作数
dp[i][j]：表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j] （代码随想录Carl老师给的定义）

class Solution {
public:    
    // 动态规划 二维dp
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size()+1,vector<int>(word2.size()+1,0));
        for(int i=1;i<=word1.size();++i) dp[i][0] = i;
        for(int j=1;j<=word2.size();++j) dp[0][j] = j;
        for(int i=1;i<=word1.size();++i) {
            for(int j=1;j<=word2.size();++j) {
                if(word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];
                // else dp[i][j] = min({dp[i][j-1]+1,dp[i-1][j]+1,dp[i-1][j-1]+1});
                else dp[i][j] = min({dp[i][j-1],dp[i-1][j],dp[i-1][j-1]})+1;
            }
        }
        return dp[word1.size()][word2.size()];
    }
};

时间复杂度: O(n * m) ,n表示word1的单词长度，m表示word2的单词长度
空间复杂度: O(n * m)

（2）二维dp 优化空间复杂度

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(2,vector<int>(word2.size()+1,0));
        for(int j=1;j<=word2.size();++j) dp[0][j] = j;
        for(int i=1;i<=word1.size();++i) {
            dp[i%2][0] = i;
            for(int j=1;j<=word2.size();++j) {
                if(word1[i-1] == word2[j-1]) dp[i%2][j] = dp[(i-1)%2][j-1];
                else dp[i%2][j] = min({dp[i%2][j-1],dp[(i-1)%2][j],dp[(i-1)%2][j-1]})+1;
            }
        }
        return dp[word1.size() % 2][word2.size()];
    }
};

时间复杂度: O(n * m) ,n表示word1的单词长度，m表示word2的单词长度
空间复杂度: O(m)

（3）一维dp 优化空间复杂度

class Solution {
public:
    // 动态规划 一维dp 优化空间复杂度
    int minDistance(string word1, string word2) {
        vector<int> dp(word2.size()+1,0);
        for(int j=1;j<=word2.size();++j) dp[j] = j;
        for(int i=1;i<=word1.size();++i) {
            int pre = dp[0];
            dp[0] = i;
            for(int j=1;j<=word2.size();++j) {
                int tmp = dp[j];
                if(word1[i-1] == word2[j-1]) dp[j] = pre;
                else dp[j] = min({dp[j-1],dp[j],pre})+1;
                pre = tmp;
            }
        }
        return dp[word2.size()];
    }
};

时间复杂度: O(n * m) ,n表示word1的单词长度，m表示word2的单词长度
空间复杂度: O(m)

图文参考b站视频和文章：

[轻松掌握动态规划]6.编辑距离_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1sA411B73r/?spm_id_from=333.880.my_history.page.click

代码随想录 (programmercarl.com)https://www.programmercarl.com/0072.%E7%BC%96%E8%BE%91%E8%B7%9D%E7%A6%BB.html#%E6%80%9D%E8%B7%AF 动态规划终极绝杀！ LeetCode：72.编辑距离_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1qv4y1q78f/?spm_id_from=333.788&vd_source=a934d7fc6f47698a29dac90a922ba5a3

来自b站代码随想录的课堂截图：