基于Eigen的位姿转换

news2024/10/5 17:28:12

       位姿中姿态的表示形式有很多种，比如：旋转矩阵、四元数、欧拉角、旋转向量等等。这里基于Eigen实现四种数学形式的相互转换功能。本文利用Eigen实现上述四种形式的相互转换。我这里给出一个SE3（4*4）(先平移、再旋转)的构建方法：

Eigen::Isometry3f T1 = Eigen::Isometry3f::Identity(); // 这一句千万别掉
// <1> 初始化R
Eigen::Matrix3f R;
// 按照 ZYX 顺序旋转
R = Eigen::AngleAxisf(3.14159 / 4, Eigen::Vector3f::UnitX()) *
            Eigen::AngleAxisf(0, Eigen::Vector3f::UnitY()) *
            Eigen::AngleAxisf(0, Eigen::Vector3f::UnitZ());
// <2> 初始化t
Eigen::Vector3f t(0.0, 0.0, 4.0);
// <3> 构建T = (R|t)
T1.rotate(R);
T1.pretranslate(t); // 这一句别搞错
//T1.translate(t);
std::cout << "T1 = " <<T1.matrix() <<std::endl;

打印结果：

T1 =         1         0         0         0
            0  0.707107 -0.707106         0
            0  0.707106  0.707107         4
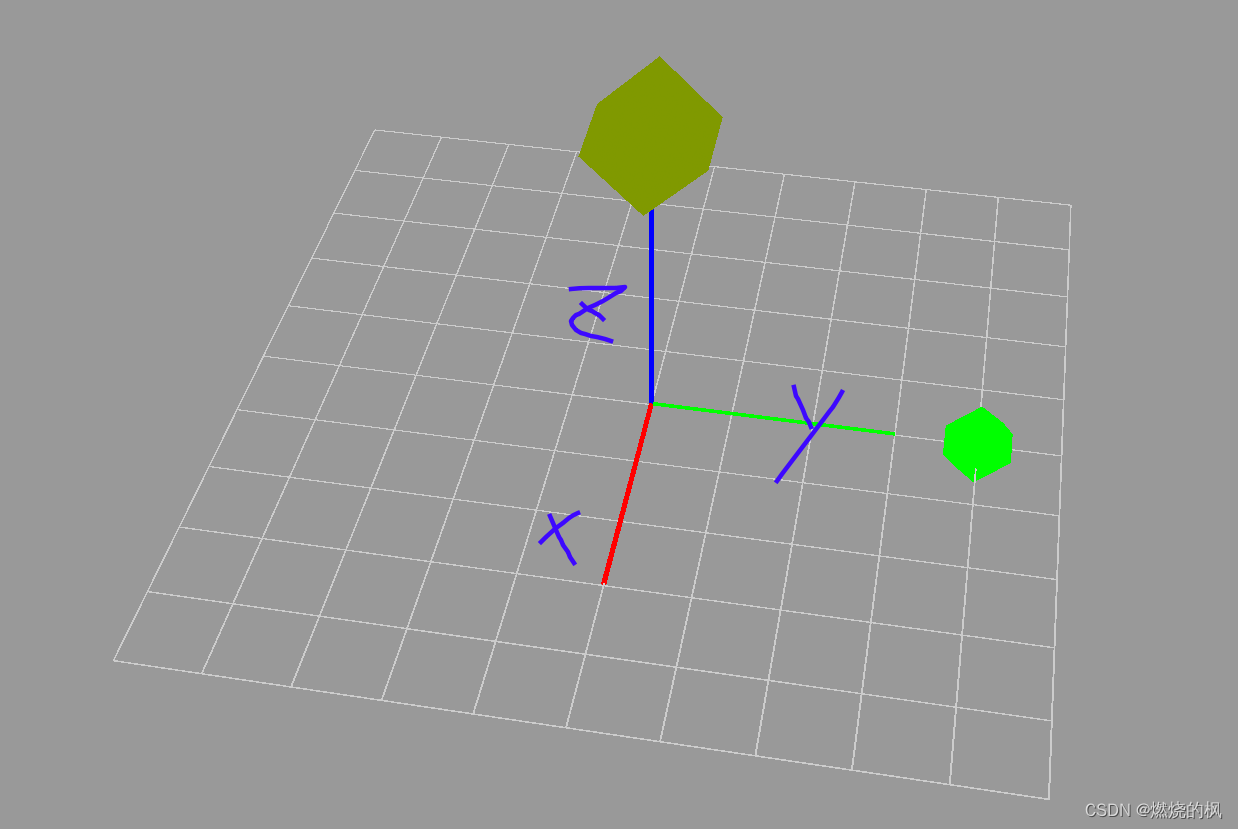
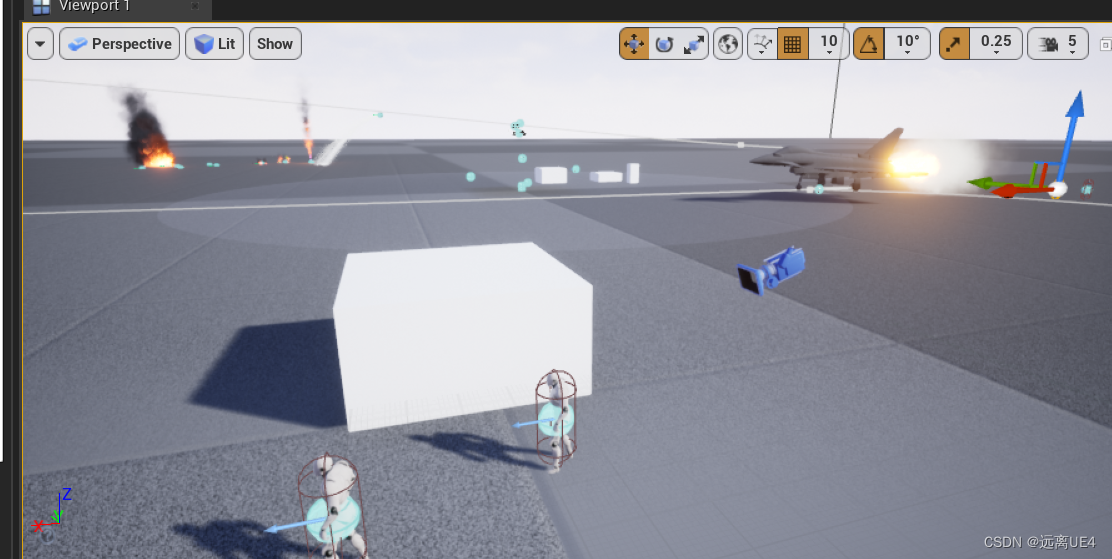
            0         0         0         1

下面的黄色立方体，相对坐标系位置为：(0 0 4)，绕x轴旋转pi /4，得到绿色立方体

以下是在本地word中笔记的截图：

Pose.h(类Pose声明)

#pragma once
#ifndef POSE_H
#define POSE_H

#include<Eigen/Core>
#include<Eigen/Geometry>

// namespace Geometry

class Pose
{
public:
    Pose();

    Pose& operator= (const Pose& pose);

    // construct from rotation
    Pose(const Eigen::Matrix3d& rotation);

    // construct from quaternion
    Pose(const Eigen::Quaterniond& quaternion);

    // construct from angle axisd
    Pose(const Eigen::AngleAxisd& angle_axis);

    // construct from euler angle
    Pose(const Eigen::Vector3d& euler_angle);

    ~Pose();

    // return rotation
    Eigen::Matrix3d rotation() const;

    // return quaterniond
    Eigen::Quaterniond quaternion() const;

    // return angle axisd
    Eigen::AngleAxisd angle_axis() const;

    // return euler angle
    Eigen::Vector3d euler_angle() const;

private:

    Eigen::Matrix3d rotation_;       // 旋转矩阵

    Eigen::Quaterniond quaternion_;  // 四元数

    Eigen::AngleAxisd angle_axis_;  // 角轴

    Eigen::Vector3d euler_angle_;    // 欧拉角 roll(X轴)  pitch(Y轴) yaw(Z轴)

};

// 姿态组合
Eigen::Isometry3d compose(const Eigen::Isometry3d& T1, const Eigen::Isometry3d& T2);

// 求逆
Eigen::Isometry3d inverse(const Eigen::Isometry3d& T);


#endif // !POSE_H

Pose.cpp(类Pose的实现)

#include "Pose.h"


Pose::Pose()
{}


Pose& Pose::operator= (const Pose& pose)
{
    this->rotation_    = pose.rotation();
    this->quaternion_  = pose.quaternion();
    this->angle_axis_ = pose.angle_axis();
    this->euler_angle_ = pose.euler_angle();
    return *this;
}

//
Pose::Pose(const Eigen::Matrix3d& rotation) :
    rotation_(rotation),
    quaternion_(Eigen::Quaterniond(rotation_)),
    angle_axis_(Eigen::AngleAxisd(rotation_)),
    euler_angle_(rotation_.eulerAngles(0, 1, 2))
{}

Pose::Pose(const Eigen::Quaterniond& quaternion)
{
    quaternion.normalized();

    this->rotation_    = quaternion.toRotationMatrix();
    this->quaternion_  = Eigen::Quaterniond(rotation_);
    this->angle_axis_ = Eigen::AngleAxisd(rotation_);
    this->euler_angle_ = rotation_.eulerAngles(0, 1, 2);
}


Pose::Pose(const Eigen::AngleAxisd& angle_axis) :
    rotation_(angle_axis),
    quaternion_(Eigen::Quaterniond(rotation_)),
    angle_axis_(Eigen::AngleAxisd(rotation_)),
    euler_angle_(rotation_.eulerAngles(0, 1, 2))
{}


Pose::Pose(const Eigen::Vector3d& euler_angle) :
    rotation_(Eigen::AngleAxisd(euler_angle.x(), Eigen::Vector3d::UnitX()) * // note: ZYX
                Eigen::AngleAxisd(euler_angle.y(), Eigen::Vector3d::UnitY()) *
              Eigen::AngleAxisd(euler_angle.z(), Eigen::Vector3d::UnitZ())),
    quaternion_(Eigen::Quaterniond(rotation_)),
    angle_axis_(Eigen::AngleAxisd(rotation_)),
    euler_angle_(rotation_.eulerAngles(0, 1, 2))
{}


Pose::~Pose()
{}


Eigen::Matrix3d Pose::rotation() const
{
    return this->rotation_;
}


Eigen::Quaterniond Pose::quaternion() const
{
    return this->quaternion_;
}


Eigen::AngleAxisd Pose::angle_axis() const
{
    return this->angle_axis_;
}


Eigen::Vector3d Pose::euler_angle() const
{
    return this->euler_angle_;
}


Eigen::Isometry3d compose(const Eigen::Isometry3d& T1, const Eigen::Isometry3d& T2)
{
    return T1 * T2;
}

Eigen::Isometry3d inverse(const Eigen::Isometry3d& T)
{
    return T.inverse();
}

test_pose.cpp

#include<iostream>
using namespace std;

#include"Pose.h"
const double M_PI = 3.1415926535;

// 对于同一个姿态，从不同的数学形式(旋转矩阵、四元数、欧拉角、角轴)构造类Pose
// 依次得到 pose1 pose2 pose3 pose4
void testClassPose(const Eigen::Matrix3d& R1)
{

    Pose pose1(R1);
    cout << "旋转矩阵 = " << endl; cout << pose1.rotation() << endl;
    cout << "欧拉角 = " << endl;   cout << pose1.euler_angle().transpose()*(180 / M_PI) << endl;
    cout << "四元数 = " << endl;   cout << pose1.quaternion().coeffs().transpose() << endl;
    cout << "角轴 = " << endl;
    cout << pose1.angle_axis().angle()* (180 / M_PI) <<" " << pose1.angle_axis().axis().transpose() <<endl;
    cout << "-----------------------------" << endl;

    Pose pose2(pose1.euler_angle());
    cout << "旋转矩阵 = " << endl; cout << pose2.rotation() << endl;
    cout << "欧拉角 = " << endl;   cout << pose2.euler_angle().transpose()*(180 / M_PI) << endl;
    cout << "四元数 = " << endl;   cout << pose2.quaternion().coeffs().transpose() << endl;
    cout << "角轴 = " << endl;
    cout << pose2.angle_axis().angle()* (180 / M_PI) << " " << pose2.angle_axis().axis().transpose() << endl;
    cout << "-----------------------------" << endl;


    Pose pose3(pose1.angle_axis());
    cout << "旋转矩阵 = " << endl; cout << pose3.rotation() << endl;
    cout << "欧拉角 = " << endl;   cout << pose3.euler_angle().transpose()*(180 / M_PI) << endl;
    cout << "四元数 = " << endl;   cout << pose3.quaternion().coeffs().transpose() << endl;
    cout << "角轴 = " << endl;
    cout << pose3.angle_axis().angle()* (180 / M_PI) << " " << pose3.angle_axis().axis().transpose() << endl;
    cout << "-----------------------------" << endl;


    Pose pose4 = pose3;
    cout << "旋转矩阵 = " << endl; cout << pose4.rotation() << endl;
    cout << "欧拉角 = " << endl;   cout << pose4.euler_angle().transpose()*(180 / M_PI) << endl;
    cout << "四元数 = " << endl;   cout << pose4.quaternion().coeffs().transpose() << endl;
    cout << "角轴 = " << endl;
    cout << pose4.angle_axis().angle()* (180 / M_PI) << " " << pose4.angle_axis().axis().transpose() << endl;
    cout << "-----------------------------" << endl;


}

// 测试求逆、compose等
void testTheOthers(Eigen::Matrix3d R1, Eigen::Vector3d t1,
                   Eigen::Matrix3d R2, Eigen::Vector3d t2)
{
    // 初始化T1
    Eigen::Isometry3d T1 = Eigen::Isometry3d::Identity();
    T1.prerotate(R1); T1.pretranslate(t1);
    cout << "T1" << endl; cout << T1.matrix() << endl;

    // 初始化T2
    Eigen::Isometry3d T2 = Eigen::Isometry3d::Identity();
    T2.prerotate(R2); T2.pretranslate(t2);
    cout << "T2" << endl; cout << T2.matrix() << endl;

    // 求逆
    Eigen::Isometry3d T1_inverse = inverse(T1);
    cout << "T1_inverse = " << endl; cout << T1_inverse.matrix() << endl;

    // compose
    Eigen::Isometry3d T12 = compose(T1, T2);
    cout << "T12 = " << endl; cout <<  T12.matrix() << endl;


    /*cout << "Rotation = " << endl;
    cout << T1.rotation() * T2.rotation() << endl;

    cout << "Translation = " << endl;
    cout << T1.rotation() * T2.translation() + T1.translation() << endl;*/

}

int main()
{
    Eigen::Matrix3d R1; //R1
    R1 = Eigen::AngleAxisd((30.0 / 180) * M_PI, Eigen::Vector3d::UnitX())*
         Eigen::AngleAxisd((25.0 / 180) * M_PI, Eigen::Vector3d::UnitY())*
         Eigen::AngleAxisd((27.0 / 180) * M_PI, Eigen::Vector3d::UnitZ());
    Eigen::Vector3d t1(1.2, 0.234, 2.3);//t1

    Eigen::Matrix3d R2; //R2
    R2 = Eigen::AngleAxisd((23.0 / 180) * M_PI, Eigen::Vector3d::UnitX())*
         Eigen::AngleAxisd((33.0 / 180) * M_PI, Eigen::Vector3d::UnitY())*
         Eigen::AngleAxisd((89.0 / 180) * M_PI, Eigen::Vector3d::UnitZ());
    Eigen::Vector3d t2(0.1, 0.4, 0.1); //t2

    // <1> test Class Pose
    testClassPose(R1);

    // <2> test halcon's api
    testTheOthers(R1, t1, R2, t2);


    return 1;
}

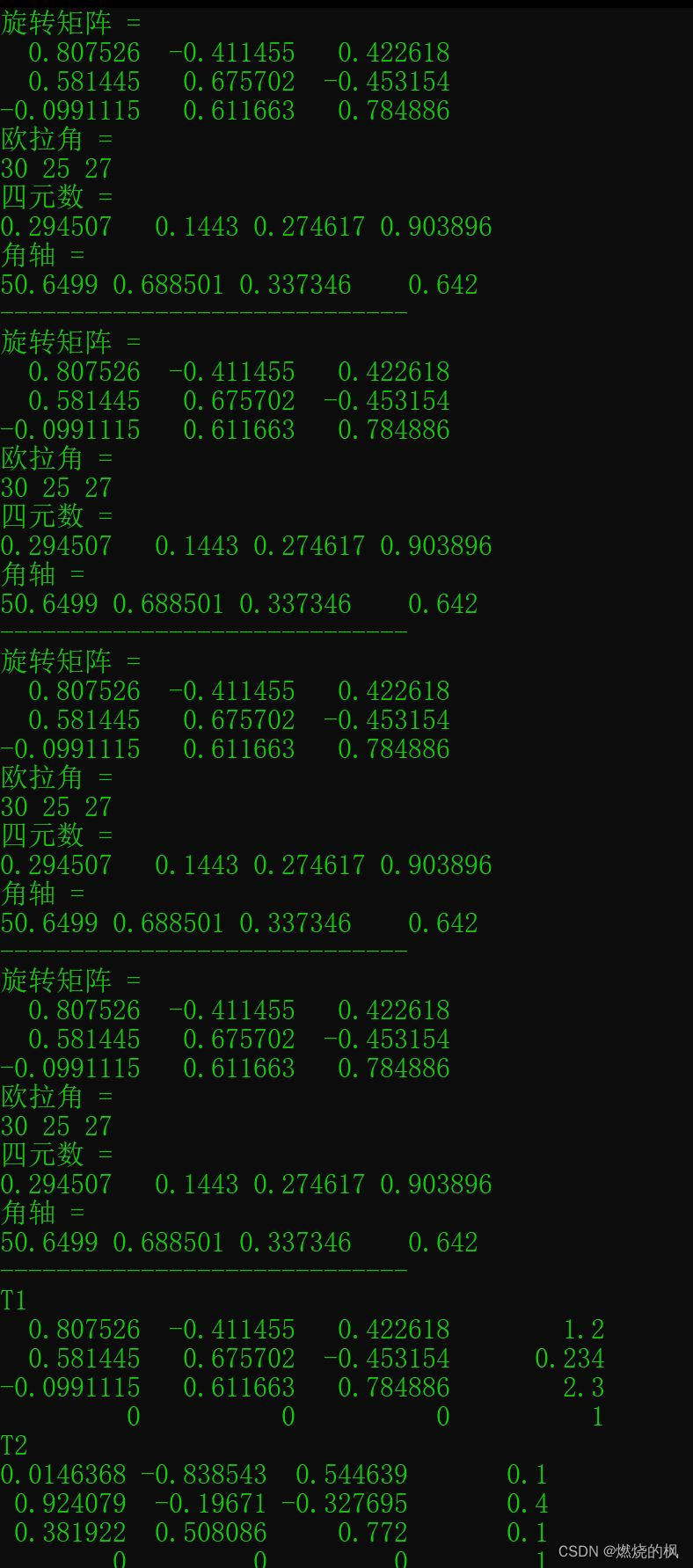
可以看到，同一个姿态，不同的表达形式，他们之间相互转换之后结果数值一致。

        写在最后，一个T为4×4的变换矩阵，如果旋转分量是欧式正交群，那个这个T为：欧式变换；否者为：仿射变换。如果一个旋转矩阵，不是SO3，那么可以将其转为四元数，接着归一化，再转为旋转矩阵，这样结果就属于SO3。同理，如果一个四元数，最好对齐进行归一化处理，再转为其他形式。例如：构造函数Pose(const Eigen::Quaterniond& quaternion); 其实现中比其他构造函数多了归一化这一步骤；即：quaternion.normalized();

       请看测试案例test3()，我们在第4或第5行进行四元数归一化，那么24行打印出来的矩阵就是单位阵。（不归一化，则不是单位阵）

void test3()
{
    Eigen::Quaterniond q = { 0.1,0.35,0.2,0.3 };
    //q.normalize();
    Eigen::Matrix3d R = q.normalized().toRotationMatrix();

    cout << "R = " << endl;
    cout << R << endl;
    cout << endl;

    Eigen::Matrix3d R_transpose = R.transpose();
    cout << "R.transpose = " << endl;
    cout << R_transpose << endl;
    cout << endl;

    Eigen::Matrix3d R_inverse = R.inverse();

    cout << "R.inverse = " << endl;
    cout << R_inverse << endl << endl;
    cout << endl;

    Eigen::Matrix3d ret = R * R.transpose();
    cout << "ret = " << endl;
    cout << ret << endl << endl;
    cout << endl;
}

运行结果：

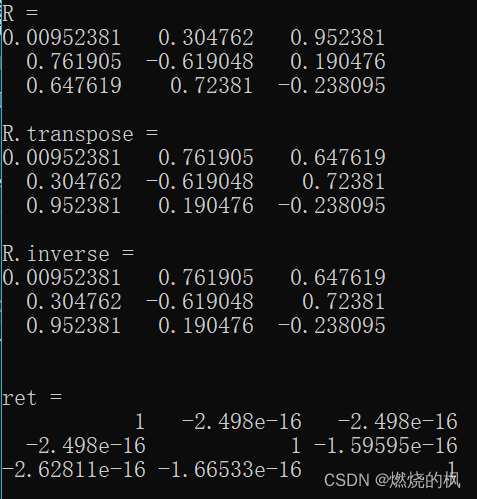
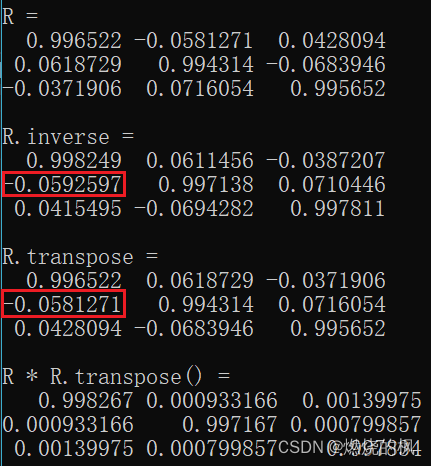
        现在，如果给定一个旋转矩阵（如果你是随机测试，请你参考博客开始部分公式，每个元素是有取值范围的，给出的数字不要太离谱）；如下测试案例test4。第8行在底层有四元数归一化操作，所以你看下面效果图，R * R.tranpose() 近似为一个单位矩阵。

void test4()
{
    Eigen::Matrix3d R;
    R << 0.74, 0.08, 0.25,
        0.2, 0.575, 0.05,
        0.17, 0.19, 0.675;
    Pose p1(R);
    Pose p2(p1.quaternion()); // Pose中，针对从四元数构造，默认有归一化功能
    R = p2.rotation();
    cout << "R = " << endl;
    cout << R << endl;
    cout << endl;

    cout << "R.inverse = " << endl;
    cout << R.inverse() << endl;
    cout << endl;

    cout << "R.transpose = " << endl;
    cout << R.transpose() << endl;
    cout << endl;

    cout << "R * R.transpose() = " << endl;
    cout << R * R.transpose() << endl;
    cout << endl;
}

运行结果：

        其中，R表示旋转，用旋转向量来描述（欧拉角有周期性和方向锁的问题，四元数有单位向量的约束，旋转矩阵冗余度太高且有各个基需要是单位正交的约束）；t表示平移，用平移向量来描述。R和t均采用无约束的向量进行描述，于是也均可以通过网络的学习来得到。因为R和t共有六个自由度，因此姿态估计又称为6D姿态估计。

注：旋转向量的方向代表旋转轴，模长代表旋转角的大小，旋转方向为逆时针。

        Eigen对于 translate 与 pretranslate的区别？（先平移、再旋转和 先旋转、再平移，有何区别？）可以看看这个：https://zhuanlan.zhihu.com/p/165020637

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1093517.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Ubuntu - 安装Docker

Ubuntu - 安装Docker

在Ubuntu上安装Docker分为以下几个步骤&#xff1a; 更新包列表&#xff1a; sudo apt update 安装依赖包&#xff0c;以便允许apt使用HTTPS&#xff1a; sudo apt install apt-transport-https ca-certificates curl software-properties-common 添加Docker官方GPG密钥&a…
阅读更多...
在命令行下使用Apache Ant

在命令行下使用Apache Ant

Apache Ant的帮助文档 离线帮助文档 在<ant的安装目录>/manual下是离线帮助文档 双击index.html可以看到帮助文档的内容&#xff1a; 在线帮助文档 最新发布版本的帮助文档https://ant.apache.org/manual/index.html Apache Ant的命令 ant命令行格式 ant [opt…
阅读更多...
在 Windows 平台上启动 MATLAB

在 Windows 平台上启动 MATLAB

目录 在 Windows 平台上启动 MATLAB 选择 MATLAB 图标 从 Windows 系统命令行调用 matlab 从 MATLAB 命令提示符调用 matlab 打开与 MATLAB 相关联的文件 从 Windows 资源管理器工具中选择 MATLAB 可执行文件 在 Windows 平台上启动 MATLAB 选择以下一种方式启动 MATLAB…
阅读更多...
6.串口、时钟

6.串口、时钟

预备知识 CC2530在正常运行的时候需要一个高频时钟信号和一个低频的时钟信号 高频时钟信号&#xff0c;主要供给CPU&#xff0c;保证程序的运行。 低频时钟信号&#xff0c;主要供给看门狗、睡眠定时器等偏上外设。 CC2530时钟信号的来源&#xff1a; 高频信号有2个&#xff0…
阅读更多...
【C++】：初阶模板

【C++】：初阶模板

朋友们、伙计们&#xff0c;我们又见面了&#xff0c;本期来给大家解读一下有关Linux的基础知识点&#xff0c;如果看完之后对你有一定的启发&#xff0c;那么请留下你的三连&#xff0c;祝大家心想事成&#xff01; C 语 言 专 栏&#xff1a;C语言&#xff1a;从入门到精通 数…
阅读更多...
Stirling-PDF：一款优秀的开源PDF处理工具

Stirling-PDF：一款优秀的开源PDF处理工具

最近我的朋友大雄需要将一个PDF转换为Word文档。于是他在网上尝试了多个PDF转换的在线工具&#xff0c;但要么需要会员&#xff0c;要么需要登录等繁琐操作&#xff0c;而且我们的文件也存在泄漏等安全隐患。因此&#xff0c;他向我咨询是否有可私有化部署且易于使用的PDF在线工…
阅读更多...
字符函数和字符串函数2（C语言进阶）

字符函数和字符串函数2（C语言进阶）

字符函数和字符串函数2 三.长度受限制的字符串函数介绍1.strncpy2.strncat3.strncmp 四.字符串查找1.strstr2.strtok 五.错误信息报告1.strerror 六.字符操作七.内存操作函数1.memcpy2.memmove3.memset4.memcmp 三.长度受限制的字符串函数介绍 1.strncpy char * strncpy ( ch…
阅读更多...
8.简易无线通信

8.简易无线通信

预备知识 Zigbee无线通信&#xff0c;需要高频的载波来提供发射效率&#xff0c;Zigbee模块之间要可以正常的收发&#xff0c;接收模块必须把接收频率设置和发射模块的载波频率一致。Zigbee有27个载波可以进行通信&#xff0c;载波叫做信道&#xff08;无线通信的通道&#xf…
阅读更多...
UE4 EQS环境查询 学习笔记

UE4 EQS环境查询 学习笔记

EQS环境查询对应Actor的范围 EQS环境查询查询对应的类 查询到即有一个蓝色的球在Actor上&#xff0c;里面有位置信息等等 在行为树运行EQS&#xff0c;按键&#xff08;‘&#xff09;可以看到Player的位置已经被标记 运行对应的EQS在这里放如EQS就可以了 Generated Point&…
阅读更多...
2023年中国分布式光纤传感产量、需求量及行业市场规模分析[图]

2023年中国分布式光纤传感产量、需求量及行业市场规模分析[图]

分布式光纤传感器中的光纤能够集传感、传输功能于一体&#xff0c;能够完成在整条光纤长度上环境参量的空间、时间多维连续测量&#xff0c;具有结构简单、易于布设、性价比高、易实现长距离等独特优点&#xff0c;常用的分布式光纤传感器有光时域反射仪、布里渊分析仪、喇曼反…
阅读更多...
【AI视野·今日Robot 机器人论文速览 第五十四期】Fri, 13 Oct 2023

【AI视野·今日Robot 机器人论文速览 第五十四期】Fri, 13 Oct 2023

AI视野今日CS.Robotics 机器人学论文速览 Fri, 13 Oct 2023 Totally 45 papers &#x1f449;上期速览✈更多精彩请移步主页 Interesting: &#x1f4da;AI与机器人安全, 从攻击界面、伦理法律和人机交互层面进行了论述。(from 密西西比大学) &#x1f4da;机器人与图机器学…
阅读更多...
Windows端口号被占用的查看方法及解决办法

Windows端口号被占用的查看方法及解决办法

Windows端口号被占用的查看方法及解决办法 Error starting ApplicationContext. To display the conditions report re-run your application with debug enabled. 2023-10-14 22:58:32.069 ERROR 6488 --- [ main] o.s.b.d.LoggingFailureAnalysisReporter : ***…
阅读更多...
Qt 布局(QLayout 类QStackedWidget 类) 总结

Qt 布局(QLayout 类QStackedWidget 类) 总结

一、QLayout类(基本布局) QLayout类是Qt框架中用于管理和排列QWidget控件的布局类。它提供了一种方便而灵活的方式来自动布局QWidget控件。QLayout类允许您以一种简单的方式指定如何安排控件&#xff0c;并能够自动处理控件的位置和大小&#xff0c;以使其适应更改的父窗口的大…
阅读更多...
【HCIA】静态路由综合实验

【HCIA】静态路由综合实验

实验要求&#xff1a; 1、R6为ISP&#xff0c;接口IP地址均为公有地址&#xff0c;该设备只能配置IP地址之后不能再对其进行任何配置 2、R1-R5为局域网&#xff0c;私有IP地址192.168.1.0/24&#xff0c;请合理分配 3、R1、R2、R4&#xff0c;各有两个环回IP地址;R5,R6各有一…
阅读更多...
基于 Kubernetes 的 Serverless PaaS 稳定性建设万字总结

基于 Kubernetes 的 Serverless PaaS 稳定性建设万字总结

作者&#xff1a;许成铭&#xff08;竞霄&#xff09; 数字经济的今天&#xff0c;云计算俨然已经作为基础设施融入到人们的日常生活中&#xff0c;稳定性作为云产品的基本要求&#xff0c;研发人员的技术底线&#xff0c;其不仅仅是文档里承诺的几个九的 SLA 数字&#xff0c…
阅读更多...
MyBatis的缓存,一级缓存，二级缓存

MyBatis的缓存,一级缓存，二级缓存

10、MyBatis的缓存 10.1、MyBatis的一级缓存 一级缓存是SqlSession级别的&#xff0c;通过同一个SqlSession对象 查询的结果数据会被缓存&#xff0c;下次执行相同的查询语句&#xff0c;就 会从缓存中&#xff08;缓存在内存里&#xff09;直接获取&#xff0c;不会重新访问…
阅读更多...
c++string类的赋值问题

c++string类的赋值问题

来看问题&#xff1a; 为什么呢&#xff1f;是因为定义string a""时候a没有占用空间&#xff0c;所以没有a[0],a[1],a[3]。如果说string a"hhhhhh"&#xff0c;那么图中a[0],a[1],a[3]就有效了。正确的做法是用连接&#xff0c;或者是定义时写成string a(6…
阅读更多...
爬虫 | 正则、Xpath、BeautifulSoup示例学习

爬虫 | 正则、Xpath、BeautifulSoup示例学习

文章目录 &#x1f4da;import requests&#x1f4da;import re&#x1f4da;from lxml import etree&#x1f4da;from bs4 import BeautifulSoup&#x1f4da;小结 契机是课程项目需要爬取一份数据&#xff0c;于是在CSDN搜了搜相关的教程。在博主【朦胧的雨梦】主页学到很多…
阅读更多...
vsc连接wsl安装vsc时遇到权限问题的解决方案

vsc连接wsl安装vsc时遇到权限问题的解决方案

当点击左下角的连接 遇到下面的权限提示时 mkdir: cannot create directory ‘/home/xxx(用户名)/.vscode-server’: Permission denied 可以新建文件 /etc/wsl.conf&#xff0c;并拷贝如下内容 # Automatically mount Windows drive when the distribution is launched [aut…
阅读更多...
面试总结之Java基础

面试总结之Java基础

1、反射 1.1、概述 反射&#xff1a;加载类&#xff08;通过反射将类的字节码文件加载到内存中&#xff09;&#xff0c;并允许以编程的方式解剖类中的各种成分&#xff08;成员变量、方法、构造器等&#xff09;反射需要掌握的内容&#xff1a; 1&#xff09;记载类&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023