下载压缩包：
PowerDesigner16.5压缩包
https://pan.baidu.com/s/1PxGafZUb5kcqSuPnxT4zgA?pwd=6nyz 
http://PowerDesigner16.5压缩包 提取码：6nyz
PowerDesigne破解版 找不到右边表的工具栏？
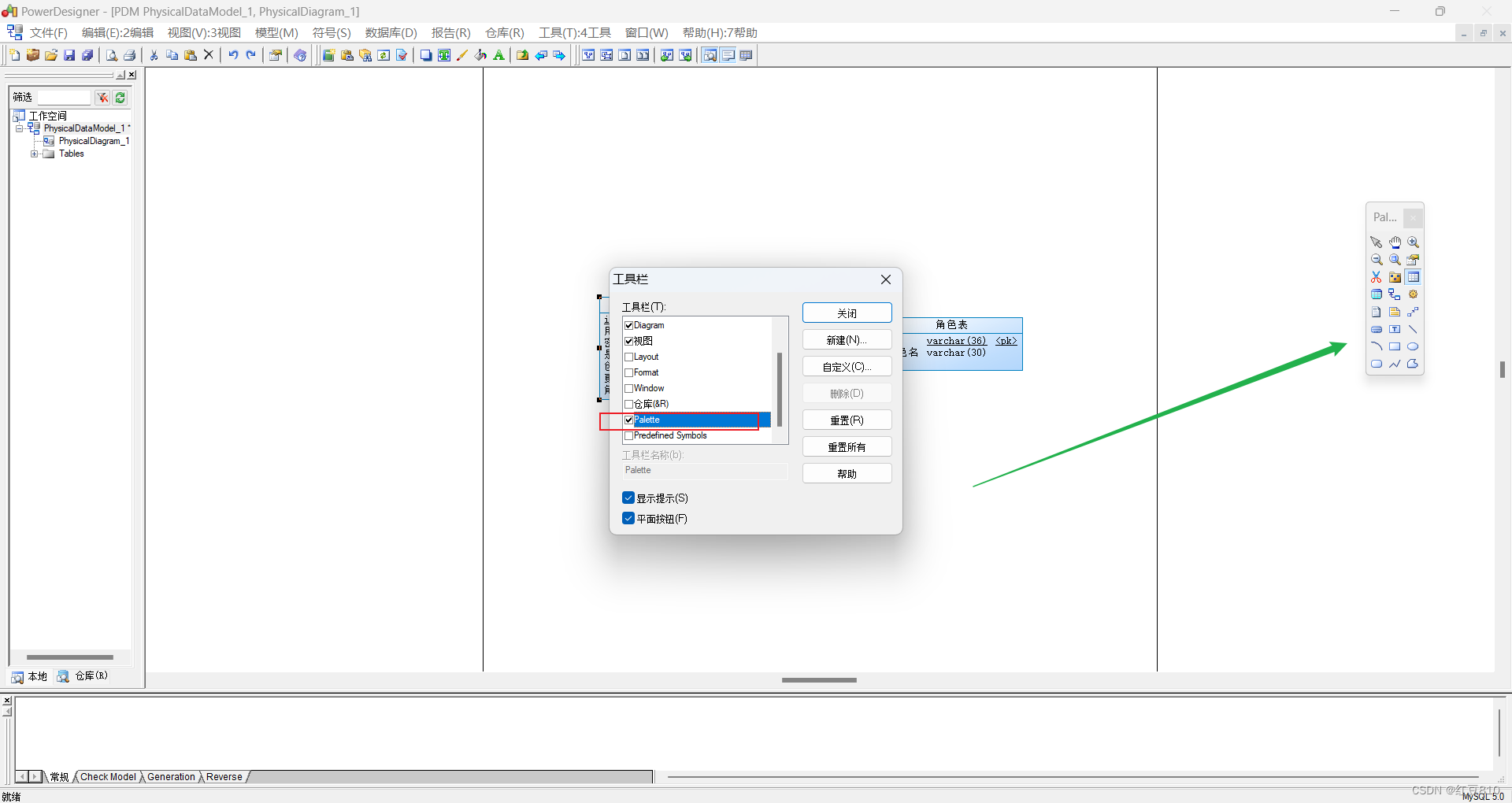
问题：PowerDesigner 快捷工具栏 palette 不见了
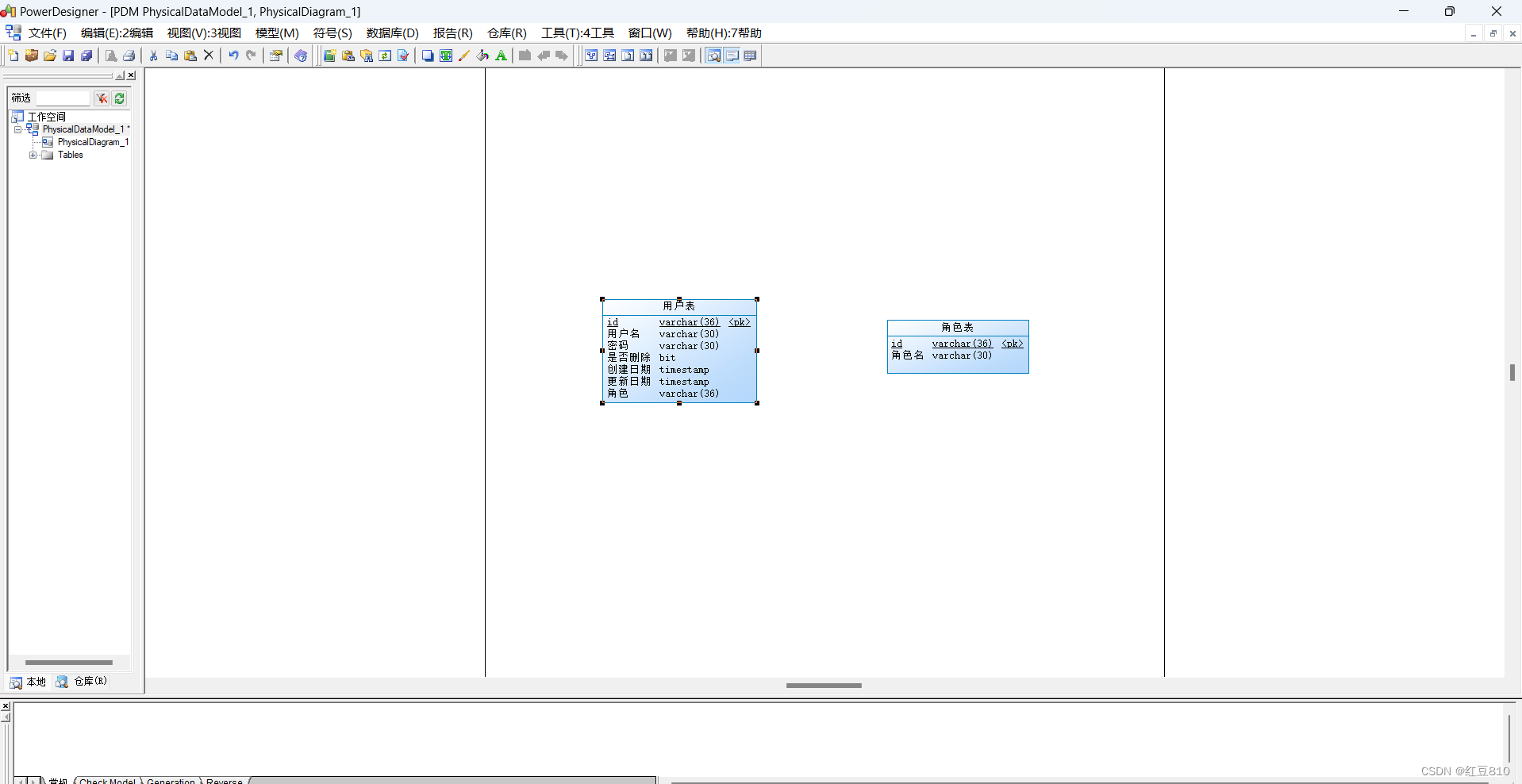
解决方法：
PowerDesigner使用过程中有时会将悬浮的工具面板关闭，关闭后可通过下面的方式使工具栏重新显示出来：
1、找到 Tools(工具栏)-> Customize Toolbars(自定义菜单和工具栏)
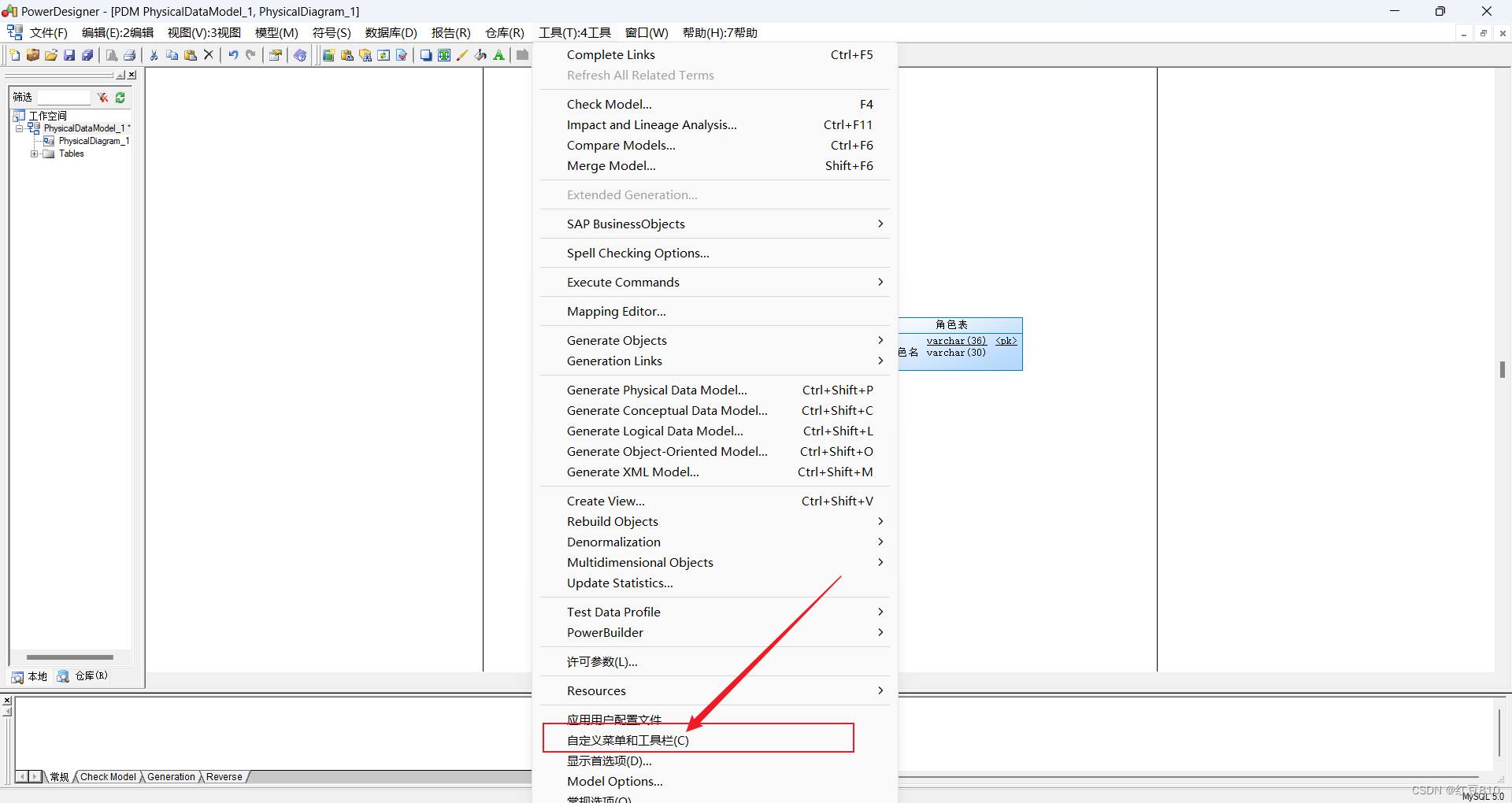
2、勾选Palette(调色板)即可
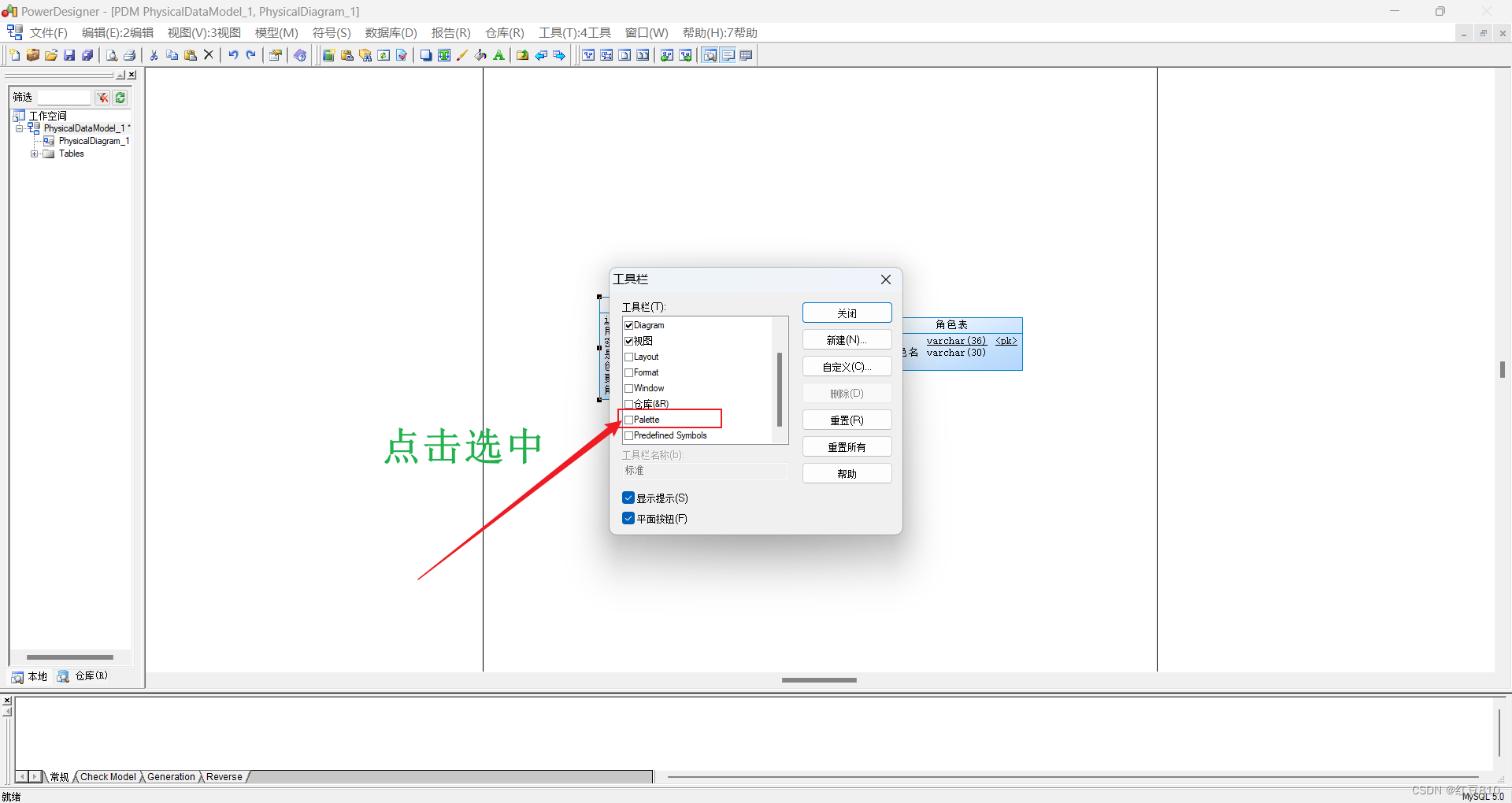
PowerDesigne破解版 右边表的工具栏已显示（如下图）
