Problem - 1108F - Codeforces

题意

思路

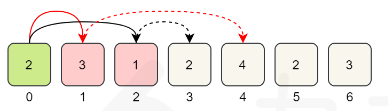
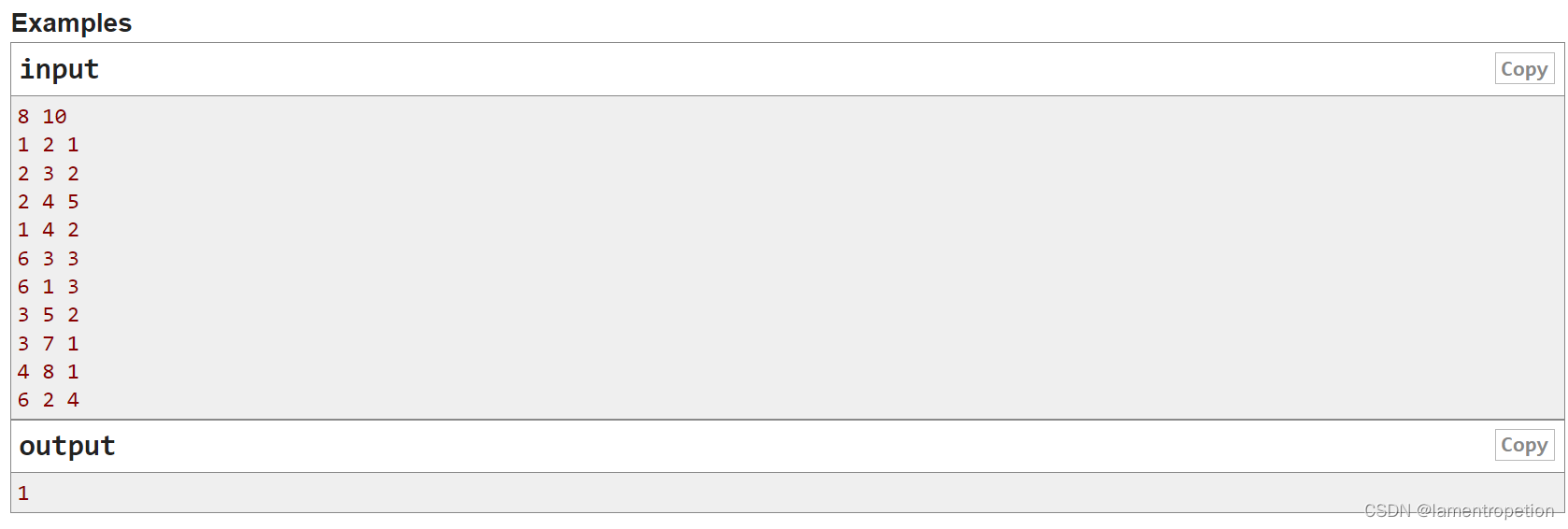
先看样例

 

这里的 MST，是把边排序之后合并至权值为3

权值为3的两条边，选其中一条即可，但是不能两条都选，这样会形成环

这启示我们，我们要操作的是和Kruskal的最后一条边权值相同的边

对于这些边，如果加了该边和现在的边集产生环，那么这边一定不能加，改边不影响MST的唯一性，因此这种边不需要操作

那么，对于加了该边之后和现有的边集不产生环的边，都要操作吗，也不是

设想样例中和5结点再连一条权值为3的边，那么该边一定要加上MST，否则就不连通了

归根到底，我们要操作的是和Kruskal最后一条边权值相同的边，且可加可不加的边

那这个就是权值相同的所有边减去一定要加和一定不能加的边数即可

Code：

#include <bits/stdc++.h>

constexpr int N = 2e5 + 10;
constexpr int M = 13;
constexpr int mod = 1e9 + 7;

int n, m;
int f[N];

int find(int x) {
    return f[x] = (x == f[x]) ? x : find(f[x]);
}
void join(int u, int v) {
    int f1 = find(u), f2 = find(v);
    if (f1 ^ f2) {
        f[f1] = f2;
    }
}
void solve() {
    std::cin >> n >> m;
    for (int i = 1; i <= n; i ++) f[i] = i;

    std::vector<std::array<int, 3> > E(m + 10);
    for (int i = 1; i <= m; i ++) {
        int u, v, w;
        std::cin >> u >> v >> w;
        E[i] = {w, u, v};
    }

    std::sort(E.begin(), E.end());
    int i = 0, j = 0;
    int ans = 0;
    while(i < E.size()) {
        while(j < E.size() && E[i][0] == E[j][0]) j ++;
        int cnt = 0;
        for (int k = i; k < j; k ++) {
            int f1 = find(E[k][1]), f2 = find(E[k][2]);
            if (f1 ^ f2) cnt ++;
        }
        for (int k = i; k < j; k ++) {
            int f1 = find(E[k][1]), f2 = find(E[k][2]);
            if (f1 ^ f2) {
                join(E[k][1], E[k][2]);
                cnt --;
            }
        }
        ans += cnt;
        i = j;
    }
    std::cout << ans << "\n";
}
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t = 1;
    while(t --) {
        solve();
    }
    return 0;
}