LeetCode 45 跳跃游戏 II

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

动态规划

dp[j]为跳到i位置所需的最少次数
实测能过但是耗时很高，恰好数据集各项数量级每超出限制，但凡0 <= nums[i] <= 1000加一点估计都过不了

提示:
1 <= nums.length <= 104
0 <= nums[i] <= 1000
题目保证可以到达 nums[n-1]

class Solution:
    def jump(self, nums: List[int]) -> int:
        length = len(nums)
        if length == 1:
            return 0
        dp = [sys.maxsize] * length
        dp[0] = 0
        for i in range(length):
            for j in range(i + 1, min(i + nums[i] + 1, length)):
                dp[j] = min(dp[j], dp[i] + 1)
        return dp[length - 1]

转换问题 + 蛮力法

class Solution:
    def jump(self, nums: List[int]) -> int:
        n = len(nums)
        maxPos, end, step = 0, 0, 0
        for i in range(n - 1):
            if maxPos >= i:
                maxPos = max(maxPos, i + nums[i])
                if i == end:
                    end = maxPos
                    step += 1
        return step

# 作者：力扣官方题解
# 链接：https://leetcode.cn/problems/jump-game-ii/
# 来源：力扣（LeetCode）
# 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

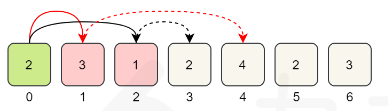
以上是官方贪心解法，感觉并不足够“贪心”，更像是暴力解法，结合上图说一下我的理解：

1. 首先一定能到，那么最多就n-1次跳跃，所以遍历每一次跳跃情况
2. 第一次跳跃，发现可以跳到1、2，没到n-1，那么必然会【跳到1或2】，跳跃次数+1
3. 第二次跳跃，会从1或2跳，可选位置，从1出发有2、3、4，从2出发有3，综合来看就是2、3、4，但是显然第一次就可以跳到2，第二次的2就可以忽略，实际上本次可忽略的位置就是本次可以跳到但是上次本就可以跳到的地方，而可忽略的位置由上次可以跳到的最远距离决定，第二次跳跃可忽略2本身及之前的位置，所以第二次跳跃【结果为3或4】，跳跃次数+1
4. 第三次跳跃，会从3或4跳，同理，从3可以跳到4、5，从4可以跳到5、6，综合可以到达4、5、6，忽略4，跳跃结果为【5或6】，显然此时就求出来了

代码写法上，应该有两层循环，第一层循环枚举的最多n-1次的跳跃次数，第二层循环，每一次跳跃中的可选位置，巧的是，把所有可选位置连起来正好是一次数组遍历，所以一层循环就可以搞定

如果将end理解为本次跳跃中可忽略数值的上限，maxPos理解为下次跳跃中可忽略数值的上限（需要由本次跳跃备选项进行遍历计算得出），一切则和官方算法一致，或许if maxPos >= i还可省略

class Solution:
    def jump(self, nums: List[int]) -> int:
        n = len(nums)
        maxPos, end, step = 0, 0, 0
        for i in range(n - 1):
            maxPos = max(maxPos, i + nums[i])
            if i == end:
                end = maxPos
                step += 1
        return step