😎前言

含义：

• 前缀和实际上就是对于长度为n的数组，我们新建立一个数组长度为n+1，第i个元素的值为前i个元素的和（包括第i个元素）。

特点：

1. 前缀和数组比原数组多一个长度。
2. 前缀和的第0个元素的值为0。
3. 根据前缀和数组的特点，求前缀和时。我们只需要用第i个元素的值+第i-1个前缀个数组的值就可能得到第i个前缀和数组的值。（这也是一种动态规划的思想）。

应用：

• 前缀和算法可以解决一些在数组中与连续有关的问题

🎄前缀和

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextInt()) { // 注意 while 处理多个 case
            int a = in.nextInt();
            int b = in.nextInt();
            System.out.println(a + b);
        }
    }
}

🚩算法思路

1. 先预处理出来⼀个「前缀和」数组：
   ⽤ dp[i] 表⽰： [1, i] 区间内所有元素的和，那么 dp[i - 1] ⾥⾯存的就是 [1,i - 1] 区间内所有元素的和，那么：可得递推公式： dp[i] = dp[i - 1] + arr[i] ；

2. 使⽤前缀和数组，「快速」求出「某⼀个区间内」所有元素的和：
   当询问的区间是 [l, r] 时：区间内所有元素的和为： dp[r] - dp[l - 1] 。

🚩代码实现

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int q = scanner.nextInt();
        int[] arr = new int[n + 1];
        for (int i = 1; i < n + 1; i++) {
            arr[i] = scanner.nextInt();
        }
        long[] dp = new long[n + 1];
        for (int i = 1; i < n + 1; i++) {
            dp[i] = dp[i - 1] + arr[i];
        }
        while (q > 0) {
            int l = scanner.nextInt();
            int r = scanner.nextInt();
            System.out.println(dp[r] - dp[l-1]);
            q--;
        }
    }
}

🌲二维前缀和

🚩题目描述

给你一个n行m列的矩阵A,下标从1开始。

接下来有q次渣询,每次查询输入4个参数x1 ,y1 ,x2,y2

请输出以(x1, y1)左角, (x2,y2) 为右下角的子矩阵的和,

• 输入描述:
  第一行包含三个整数n,m,q.
  接下来n行，行m个整数,代表矩阵的元素
  接下来q行,每行4个整数x1, y1, x2, y2,分别代表这次查询的参数

• 1≤n,m≤1000

• 1≤q≤105

• -10°≤a[i][j]≤109

• 1≤x1≤x2≤n

• 1≤y1≤y2≤m

• 输出描述:
  输出q行,珩示碴询结果。

示例1

• 输入:3 4 3
  1 2 3 4
  3 2 1 0
  1 5 7 8
  1 1 2 2
  1 1 3 3
  1 2 3 4

• 输出: 8
  2 5
  3 2

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextInt()) { // 注意 while 处理多个 case
            int a = in.nextInt();
            int b = in.nextInt();
            System.out.println(a + b);
        }
    }
}

🚩算法思路：

类⽐于⼀维数组的形式，如果我们能处理出来从 [0, 0] 位置到 [i, j] 位置这⽚区域内所有元素的累加和，就可以在 O(1) 的时间内，搞定矩阵内任意区域内所有元素的累加和。

因此我们接下来仅需完成两步即可：

📌第⼀步：搞出来前缀和矩阵

这⾥就要⽤到⼀维数组⾥⾯的拓展知识，我们要在矩阵的最上⾯和最左边添加⼀⾏和⼀列0，这样我们就可以省去⾮常多的边界条件的处理（同学们可以⾃⾏尝试直接搞出来前缀和矩阵，边界条件的处理会让你崩溃的）。处理后的矩阵就像这样

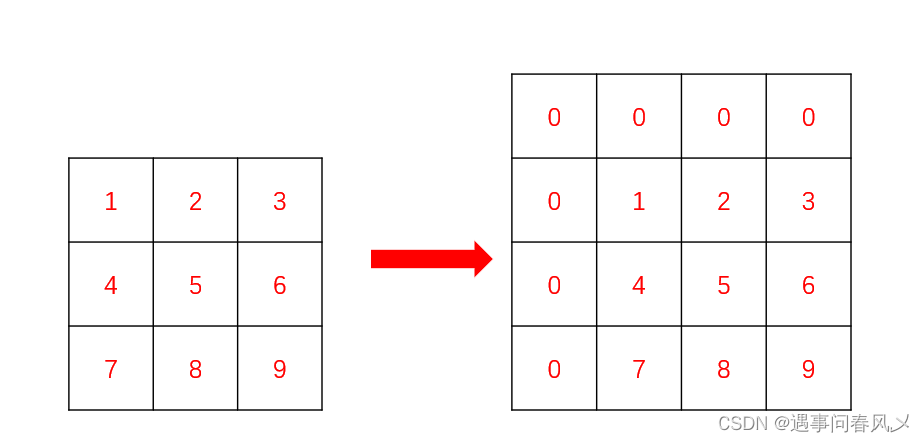
这样，我们填写前缀和矩阵数组的时候，下标直接从 1 开始，能⼤胆使⽤ i - 1 , j - 1 位置的值。

注意dp 表与原数组 matrix 内的元素的映射关系：

1. 从 dp 表到 matrix 矩阵，横纵坐标减⼀

2. 从 matrix 矩阵到 dp 表，横纵坐标加⼀

前缀和矩阵中 sum[i][j] 的含义，以及如何递推⼆维前缀和⽅程

• sum[i][j] 的含义：
  sum[i][j] 表⽰，从 [0, 0] 位置到 [i, j] 位置这段区域内，所有元素的累加和。对应下图的红⾊区域：
  
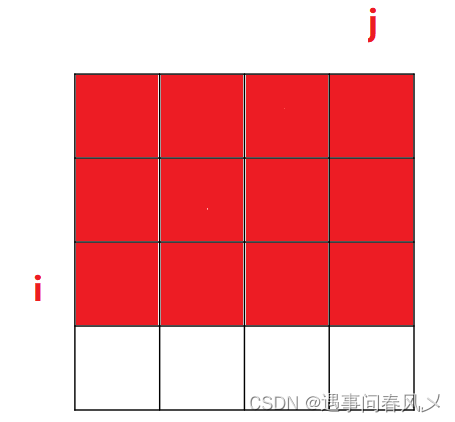
• 递推⽅程：
  其实这个递推⽅程⾮常像我们⼩学做过求图形⾯积的题，我们可以将 [0, 0] 位置到 [i, j] 位置这段区域分解成下⾯的部分
  
  sum[i][j] =红+蓝+绿+⻩，分析⼀下这四块区域：

1. ⻩⾊部分最简单，它就是数组中的 matrix[i - 1][j - 1] （注意坐标的映射关系）

2. 单独的蓝不好求，因为它不是我们定义的状态表⽰中的区域，同理，单独的绿也是；

3. 但是如果是红+蓝，正好是我们 dp 数组中 sum[i - 1][j] 的值，美滋滋；

4. 同理，如果是红+绿，正好是我们 dp 数组中 sum[i][j - 1] 的值；

5. 如果把上⾯求的三个值加起来，那就是⻩+红+蓝+红+绿，发现多算了⼀部分红的⾯积，因此再单独减去红的⾯积即可；

6. 红的⾯积正好也是符合 dp 数组的定义的，即 sum[i - 1][j - 1]

综上所述，我们的递推⽅程就是：

sum[i][j]=sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j -1]+matrix[i - 1][j - 1]

📌第⼆步：使用前缀和矩阵

题⽬的接⼝中提供的参数是原始矩阵的下标，为了避免下标映射错误，这⾥直接先把下标映射成
dp 表⾥⾯对应的下标： row1++, col1++, row2++, col2++

接下来分析如何使⽤这个前缀和矩阵，如下图（注意这⾥的 row 和 col 都处理过了，对应的正
是 sum 矩阵中的下标）：

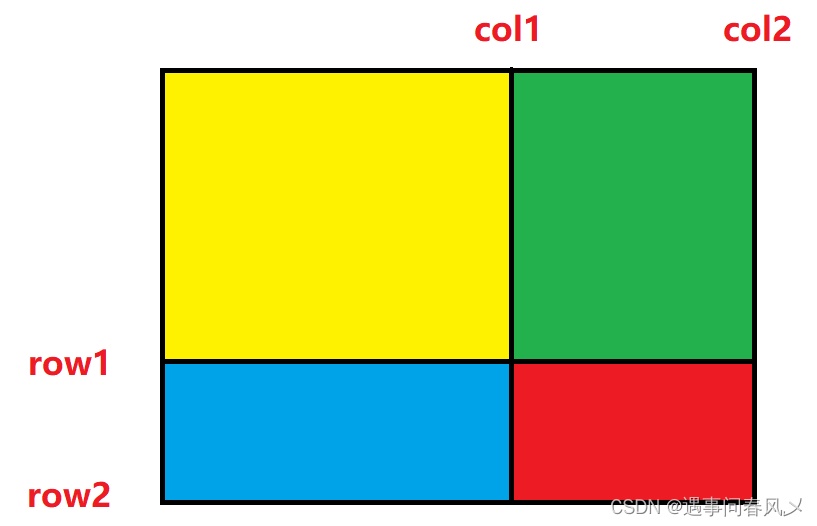
对于左上⻆ (row1, col1) 、右下⻆ (row2, col2) 围成的区域，正好是红⾊的部分。因此我们要求的就是红⾊部分的⾯积，继续分析⼏个区域：

1. ⻩⾊，能直接求出来，就是 sum[row1 - 1, col1 - 1] （为什么减⼀？因为要剔除掉 row 这⼀⾏和 col 这⼀列）

2. 绿⾊，直接求不好求，但是和⻩⾊拼起来，正好是 sum 表内 sum[row1 - 1][col2]的数据；

3. 同理，蓝⾊不好求，但是 蓝 + ⻩ = sum[row2][col1 - 1] ；

4. 再看看整个⾯积，好求嘛？⾮常好求，正好是 sum[row2][col2] ；

5. 那么，红⾊ = 整个⾯积- ⻩ - 绿 - 蓝，但是绿蓝不好求，我们可以这样减：整个⾯积 -（绿 + ⻩ ）-（蓝 + ⻩），这样相当于多减去了⼀个⻩，再加上即可

综上所述：红 = 整个⾯积 - （绿 + ⻩）- （蓝 + ⻩）+ ⻩，从⽽可得红⾊区域内的元素总和为：

sum = [row2][col2]-sum[row2][col1 - 1]-sum[row1 - 1][col2]+sum[row1 -1][col1 - 1]

🚩代码实现：

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        int q = in.nextInt();
        int[][] arr = new int[n + 1][m + 1];
        long[][] dp = new long[n + 1][m + 1];
        // 读⼊数据
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                arr[i][j] = in.nextInt();
            }
        }
        // 处理前缀和矩阵
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + arr[i][j];
            }
        }
        while (q > 0) {
            int x1 = in.nextInt();
            int y1 = in.nextInt();
            int x2 = in.nextInt();
            int y2 = in.nextInt();
            System.out.println(dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1
                               - 1]);
            q--;
        }
    }
}

⭕总结

关于《【算法优选】 前缀和专题——壹》就讲解到这儿，感谢大家的支持，欢迎各位留言交流以及批评指正，如果文章对您有帮助或者觉得作者写的还不错可以点一下关注，点赞，收藏支持一下！