前言

想要精通算法和SQL的成长之路 - 系列导航

一. 区域和检索 - 数组不可变

原题链接

思路如下：

1. 我们统计每个元素的前缀和为preSum(i) ，不包括num[i]的值。
2. 那么对于索引[left, right]之间的和，就可以利用前缀和来计算，值为：preSum(right+1) - preSum(left)

代码如下：

public class NumArray {
    int[] preSums;

    public NumArray(int[] nums) {
        int n = nums.length;
        // 计算前缀和，指 preSums[i] 在下标i之前的元素和
        preSums = new int[n + 1];
        for (int i = 0; i < n; i++) {
            preSums[i + 1] = preSums[i] + nums[i];
        }
    }

    public int sumRange(int left, int right) {
        return preSums[right + 1] - preSums[left];
    }
}

二. 二维区域和检索 - 矩阵不可变

原题链接

2.1 前缀和的计算

我们先来看下，对于任意一个元素，从下标 (0,0) 到 (i,j) 之间的区域和怎么计算。如图：

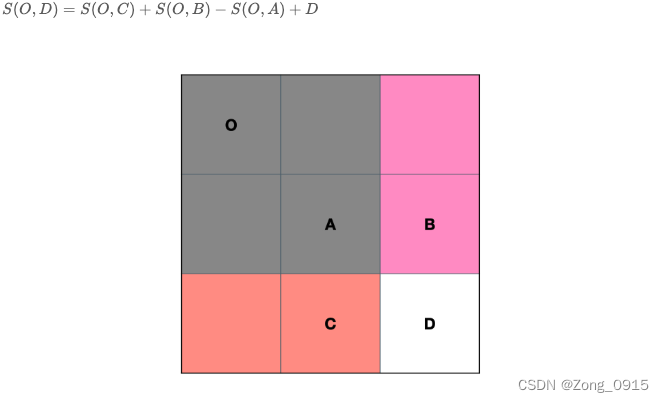
换成代码就是：

preSums[i][j] = preSums[i][j - 1] + preSums[i - 1][j] - preSums[i - 1][j - 1] + matrix[i-1][j-1];

2.2 用前缀和计算二维区域和

如图：我们想计算A到D之间的区域和：

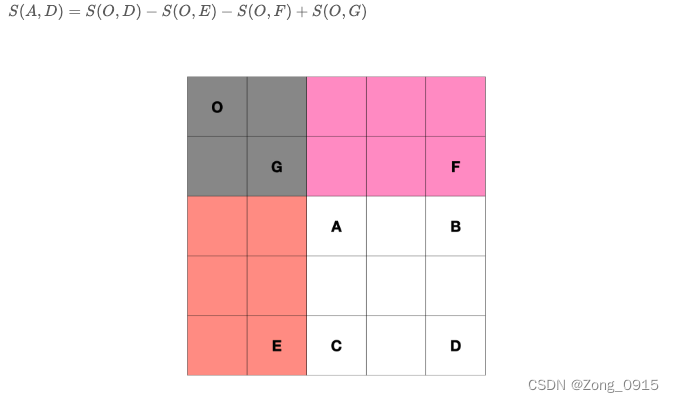
代码如下：（在设置二维数组的时候，可以增加一行和一列作为虚拟节点，数值为0）

preSums[row2+1][col2+1] - preSums[row2+1][col1] - preSums[row1][col2+1] + preSums[row1][col1];

完整代码如下：

public class NumMatrix {
    int preSums[][];

    public NumMatrix(int[][] matrix) {
        int row = matrix.length + 1;
        int col = matrix[0].length + 1;
        preSums = new int[row][col];
        // 第一列第一行的数值都是0
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                preSums[i][j] = preSums[i][j - 1] + preSums[i - 1][j] - preSums[i - 1][j - 1] + matrix[i-1][j-1];
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return preSums[row2+1][col2+1] - preSums[row2+1][col1] - preSums[row1][col2+1] + preSums[row1][col1];
    }
}

三. 矩形区域不超过 K 的最大数值和

原题链接

这题目可以在题目二的基础上，我们自行遍历，以开始节点(startRow,startCol) 为起始位置，在遍历所有情况的结束节点(endRow,endCol) 之间的区域和。满足条件：

• startRow <= endRow < row
• startCol <= endCol < col

由于是二维空间，两个节点，因此一共是4层循环：

public class Test363 {
    int preSum[][];

    public int maxSumSubmatrix(int[][] matrix, int k) {
        int row = matrix.length + 1;
        int col = matrix[0].length + 1;
        preSum = new int[row][col];
        // 结算前缀和
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                preSum[i][j] = preSum[i][j - 1] + preSum[i - 1][j] - preSum[i - 1][j - 1] + matrix[i - 1][j - 1];
            }
        }
        int max = Integer.MIN_VALUE;
        // 起始节点的横纵坐标
        for (int startRow = 1; startRow < row; startRow++) {
            for (int startCol = 1; startCol < col; startCol++) {
            	// 结束节点的横纵坐标
                for (int endRow = startRow; endRow < row; endRow++) {
                    for (int endCol = startCol; endCol < col; endCol++) {
                        // 求得两个节点之间的区域和
                        int sumRegion = sumRegion(startRow, startCol, endRow, endCol);
                        if (sumRegion <= k) {
                            max = Math.max(max, sumRegion);
                        }
                    }
                }
            }
        }
        return max;
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return preSum[row2][col2] - preSum[row2][col1 - 1] - preSum[row1 - 1][col2] + preSum[row1 - 1][col1 - 1];
    }
}