多元高斯分布的概率密度函数

f μ , Σ ( x ) = 1 ( 2 π ) D / 2 1 ∣ Σ ∣ 1 / 2 e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } f_{\mu, \Sigma}(x)=\frac{1}{(2 \pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}} exp\{-\frac{1}{2}(x-\mu)^T \Sigma ^{-1}(x-\mu)\} fμ,Σ​(x)=(2π)D/21​∣Σ∣1/21​exp{−21​(x−μ)TΣ−1(x−μ)}

这是多维高斯分布（多元正态分布）的概率密度函数。让我逐步解释这个公式的各个部分：

• $f_{\mu ,\Sigma }(x)$ 是表示多维高斯分布的概率密度函数，其中 $x$ 是一个 D 维向量（$x\in {\mathbb{R}}^D$）。
• $D$ 是数据的维度，表示向量 $x$ 包含了 D 个随机变量。
• $\mu$（mu）是一个 D 维向量，表示多维高斯分布的均值向量。
• $\Sigma$（Sigma）是一个 DxD 的协方差矩阵，表示不同维度之间的协方差关系。
• $(x-\mu {)}^T$ 表示向量 $(x-\mu )$ 的转置（transpose）。
• $|\Sigma |$ 表示协方差矩阵 $\Sigma$ 的行列式（determinant）。
• ${\Sigma }^{-1}$ 表示协方差矩阵 $\Sigma$ 的逆矩阵（inverse）。

公式的含义：

这个公式描述了 D 维多维高斯分布的概率密度。它告诉我们在给定均值 $\mu$ 和协方差矩阵 $\Sigma$ 的情况下，随机变量 $x$ 出现在空间中的概率密度。

• $\frac{1}{(2\pi {)}^{D/2}}$ 是一个标准化系数，用于确保概率密度的积分等于 1，使其成为一个合法的概率分布。
• $\frac{1}{|\Sigma {|}^{1/2}}$ 是协方差矩阵的行列式的平方根的倒数，也是标准化系数的一部分，用于调整概率密度的幅度。
• e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } exp\{-\frac{1}{2}(x-\mu)^T \Sigma ^{-1}(x-\mu)\} exp{−21​(x−μ)TΣ−1(x−μ)} 是指数部分，它包含了 $x$ 与均值 $\mu$ 的差异与协方差矩阵 $\Sigma$ 的逆之间的关系。这一部分体现了多维高斯分布的形状和方差。它与 D 维空间中的点 $x$ 到均值 $\mu$ 的距离以及协方差矩阵的逆有关。

多维高斯分布的概率密度函数用于描述多维数据的分布，通常在统计、模式识别、机器学习等领域中广泛应用。不同的协方差矩阵 $\Sigma$ 和均值向量 $\mu$ 可以产生不同形状的多维高斯分布，从而用于建模不同类型的数据分布。

多元高斯分布的最大似然估计

$L(\mu ,\Sigma )=f_{\mu ,\Sigma }(x^1)f_{\mu ,\Sigma }(x^2)f_{\mu ,\Sigma }(x^3)......f_{\mu ,\Sigma }(x^{7}9)$
${\mu }^{\ast },{\Sigma }^{\ast }=arg\underset{\mu ,\Sigma }{\max }L(\mu ,\Sigma )$

这个问题是要通过最大似然估计（MLE）来估计多元高斯分布的参数 ${\mu }^{\ast }$ 和 ${\Sigma }^{\ast }$，以使给定数据集的似然 $L(\mu ,\Sigma )$ 最大化。

在这个上下文中，$L(\mu ,\Sigma )$ 表示似然函数，它是一个关于参数 $\mu$ 和 $\Sigma$ 的函数，用于描述观测数据 $x^1,x^2,x^3,...,x^{79}$ 在给定参数下的概率。似然函数通常假设数据是根据多元高斯分布生成的，公式如下：

$$L(\mu ,\Sigma )=f_{\mu ,\Sigma }(x^1)\cdot f_{\mu ,\Sigma }(x^2)\cdot f_{\mu ,\Sigma }(x^3)\cdot ...\cdot f_{\mu ,\Sigma }(x^{79})$$

其中，$f_{\mu ,\Sigma }(x)$ 是多元高斯分布的概率密度函数，参数为 $\mu$ 和 $\Sigma$。这个似然函数表示了给定参数下观测数据集中每个数据点的出现概率，然后将它们的概率连乘得到整个数据集的似然。

你的目标是找到最大化似然函数的参数 ${\mu }^{\ast }$ 和 ${\Sigma }^{\ast }$，即：

$${\mu }^{\ast },{\Sigma }^{\ast }=\arg \underset{\mu ,\Sigma }{\max }L(\mu ,\Sigma )$$

这通常涉及到通过数值方法（如梯度上升法或牛顿法）来找到似然函数的极大值点，从而找到最可能的参数值 ${\mu }^{\ast }$ 和 ${\Sigma }^{\ast }$，以使数据集的生成概率最大化。这是多元高斯分布的最大似然估计过程。

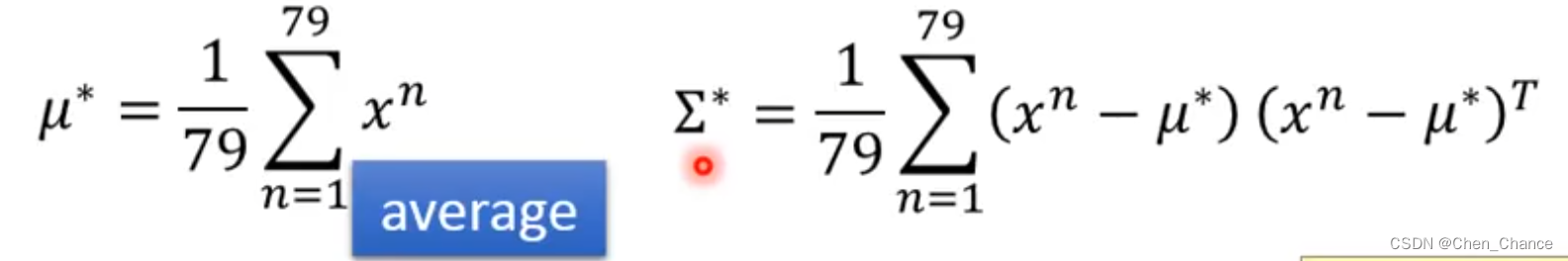
假设概率P(x|C_1)的分布服从 f μ , Σ ( x ) = 1 ( 2 π ) D / 2 1 ∣ Σ ∣ 1 / 2 e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } f_{\mu, \Sigma}(x)=\frac{1}{(2 \pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}} exp\{-\frac{1}{2}(x-\mu)^T \Sigma ^{-1}(x-\mu)\} fμ,Σ​(x)=(2π)D/21​∣Σ∣1/21​exp{−21​(x−μ)TΣ−1(x−μ)}，如何计算概率P

其中
$$\mu =\left[\begin{array}{c}75.0\\ 71.3\end{array}\right]$$

$$\Sigma =\left[\begin{array}{cc}874& 327\\ 327& 929\end{array}\right]$$

根据提供的信息，我们知道概率密度函数 $P(x|C_1)$ 符合多元高斯分布，其中参数如下：

均值向量 $\mu$：
$$\mu =\left[\begin{array}{c}75.0\\ 71.3\end{array}\right]$$

协方差矩阵 $\Sigma$：
$$\Sigma =\left[\begin{array}{cc}874& 327\\ 327& 929\end{array}\right]$$

现在，如果你想计算在给定条件 $C_1$ 下，随机变量 $x$ 落在某个区域 $[a,b]$ 内的概率，你可以使用概率密度函数来计算。具体来说，你可以计算 $P(x|C_1)$ 的积分，从 $a$ 到 $b$，如下：

$$P(a\le x\le b|C_1)={\int }_a^b\frac{1}{(2\pi {)}^{D/2}|\Sigma {|}^{1/2}}\exp \left(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\right)dx$$

在这个公式中，你可以将 $a$ 和 $b$ 设置为你感兴趣的区间的上下限。通过计算上述积分，你可以获得随机变量 $x$ 落在该区间内的条件概率。

这是一个连续分布的概率计算示例，根据具体的区间和需要计算的概率，你可以替换 $a$ 和 $b$ 来计算不同区域内的条件概率。