Namomo Summer Camp 23 Day 1 - Virtual Judge

B - Brexiting and Brentering

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
string s;
void solve() {
    cin>>s;
    int x=-1;
    for(int i=s.size()-1;i>=0;i--){
        if(s[i]=='a'||s[i]=='e'||s[i]=='i'||s[i]=='o'||s[i]=='u'){
            x=i;
            break;
        }
    }
    for(int i=0;i<=x;i++) cout<<s[i];
    cout<<"ntry"<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
//    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

A - Amusement Arcade

对于n个位置（n为奇数），（n+1)/2个人要坐满，而且是中间至少隔一个空位置，那么必然是从1开始隔一个坐一个，然后由于每一段区间我们都是尽量取中间位置，所以得保证我们选的那个位置左右两边区间长度均为2的次幂

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
bool check(int n){
    return (n>0)&&(n&(n-1))==0;
}
int n;
void solve() {
    cin>>n;
    if(n==1||n==3){
        cout<<1<<endl;
        return;
    }
    int x=1;
    for(int i=1;i<60;i++){
        x*=2;
        if(check(n-1-x)){
            cout<<x+1<<endl;
            return;
        }
    }
    cout<<"impossible"<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
//    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

I - Monty's Hall

概率

利用组合数

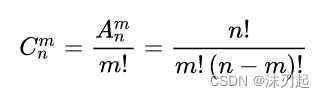
假设有3个门，选一个门的概率是1/3，然后被告知另外有一个门是空的，然后在已知另外有一个门是空的情况下，就会影响我们接下来的决策了，这样就是在两个门中二选一了，选另一个门成功的概率是1/2，而已经选的这个门是在概率为1/3的情况下选的，所以最优策略是选剩下的另一个门

设在第一次选完之后，换l个门，l=min（s，d-s-e）

第一次选中：C(s-1,d-1)/C(s,d)=s/d 换l个之后仍然选中：1-C(l-1.s-1)/C(s,l)=(s-l)/s

第一次没选中：(d-s)/s 换l个之后选中了：l/(d-s-e)

第一次选中的概率s/d也可以这么理解，就是选s个一个一个选，然后每次选中的概率为1/d，有s次机会，所有都加起来即为s/d

AC代码:

#include<bits/stdc++.h>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
int d,s,e;
void solve() {
    cin>>d>>s>>e;
    int l=min(s,d-s-e);
    double ans=1.0*(d-s)/d*l/(d-s-e)+1.0*s/d*(s-l)/s;
    printf("%.8lf\n",ans);
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
//    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}