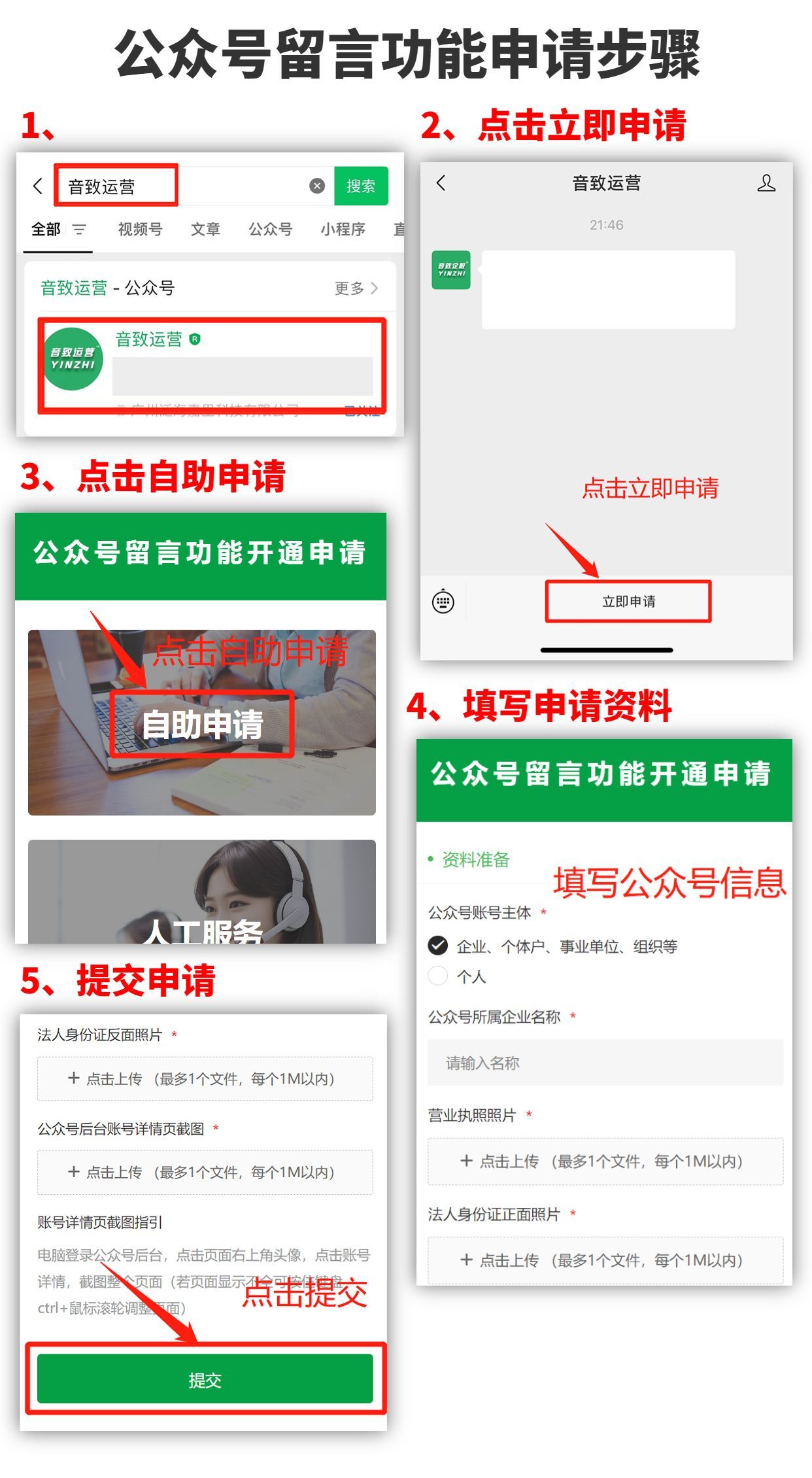
文章目录
- 模板
- 非类型模板参数
- 模板特化
- 函数模板特化
- 类模板特化
- 模板分离编译
- 反向迭代器
模板
非类型模板参数
模板参数分类类型形参与非类型形参。
类型形参即:出现在模板参数列表中,跟在class或者typename之类的参数类型名称。
非类型形参,就是用一个常量作为类(函数)模板的一个参数,在类(函数)模板中可将该参数当成常量来使用。

注意:
- 浮点数、类对象以及字符串是不允许作为非类型模板参数的。
- 非类型的模板参数必须在编译期就能确认结果。
模板特化
通常情况下,使用模板可以实现一些与类型无关的代码,但对于一些特殊类型的可能会得到一些错误的结果,需要特殊处理。比如两个数比较的话,如果参数是指针的话,就不能正常的用大于小于会比较,应该先解引用在比较,否则就会导致结果与我们预期的相反。
模板特化中分为函数模板特化与类模板特化。
函数模板特化

此时,就需要对模板进行特化。即:在原模板类的基础上,针对特殊类型所进行特殊化的实现方式。

一般情况下如果函数模板遇到不能处理或者处理有误的类型,为了实现简单通常都是将该函数直接给出。

该种实现简单明了,代码的可读性高,容易书写,因为对于一些参数类型复杂的函数模板,特化时特别给出(可以构成函数重载),因此函数模板不建议特化,建议直接使用函数重载。
类模板特化
- 全特化
全特化即是将模板参数列表中所有的参数都确定化。
template<class T1, class T2>
class Data
{
public:
Data() { cout << "Data<T1, T2>" << endl; }
private:
T1 _d1;
T2 _d2;
};
template<>
class Data<int, char>
{
public:
Data() { cout << "Data<int, char>" << endl; }
private:
int _d1;
char _d2;
};
- 偏特化
任何针对模版参数进一步进行条件限制设计的特化版本。
部分特化
将模板参数类表中的一部分参数特化。
template <class T1>
class Data<T1, int>
{
public:
Data() {cout<<"Data<T1, int>" <<endl;}
private:
T1 _d1;
int _d2;
};
偏特化并不仅仅是指特化部分参数,而是针对模板参数更进一步的条件限制所设计出来的一个特化版本。
我们可以更进一步的限制条件。
template <typename T1, typename T2>
class Data <T1*, T2*>
{
public:
Data() {cout<<"Data<T1*, T2*>" <<endl;}
private:
T1 _d1;
T2 _d2;
};
模板分离编译
什么是分离编译呢?
一个程序(项目)由若干个源文件共同实现,而每个源文件单独编译生成目标文件,最后将所有目标文件链接起来形成单一的可执行文件的过程称为分离编译模式。
我们在写模版分离编译的时候会发现出现链接错误,这是因为我们在主函数中使用了模版函数,我们有这个函数的声明,所以在编译期间不会报错,但是在实现模版函数的那个.cpp文件中并不知道我们要的是什么类型,并没有给我们实例化出相应的代码,所以会出现找不到外部符号。

解决这个问题有两种方法:
- 显示实例化
但是这种方法很局限,并不适合长久之计。 - 将声明和定义放到一个文件"xxx.hpp"里面或者xxx.h其实也是可以的。
我们一般都使用方法二。
总结
优点:
- 模板复用了代码,节省资源,更快的迭代开发,C++的标准模板库(STL)因此而产生
- 增强了代码的灵活性
缺点:
- 模板会导致代码膨胀问题,也会导致编译时间变长
- 出现模板编译错误时,错误信息非常凌乱,不易定位错误
反向迭代器
反向迭代器我们可以直接将整型迭代器复制一个,然后改一下操作,就可以实现出来我们正常人能够想到的一个反向迭代器版本。我们今天来学习学习大佬的思路,我们会发现正向迭代器和反向迭代器他们的大部分功能都是语一样的,那我们可不可以用一个正向迭代器,用我们的适配器适配出来一个反向迭代器呢?
这个反向迭代器,不仅仅使用于我们的一个容器,而是适用于我们的所有容器。

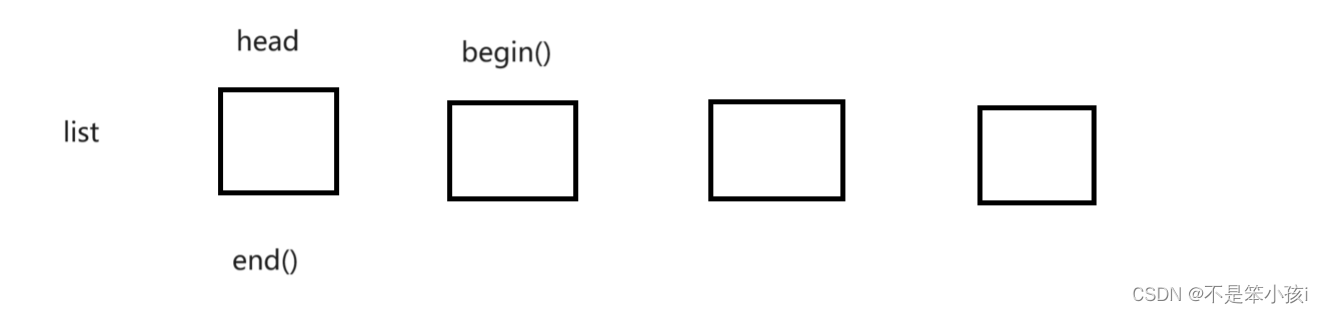
我们通过图,不难发现我们在访问之前先访问end()的前一个元素然后等到迭代器停止时,就可以拿到容器中所有元素。只不过,我们的反向迭代器是反着来的,对于++就是正向迭代器的–,所以我们就可以通过这样的一个想法,来通过一个正向迭代器适配出一个反向迭代器,但是还有一个问题就是,我们并不知道容器中元素的类型,其实这个也好说,我们在实例化模板是直接传过来就可以了。类似于正向迭代器的const于非const版本一样。这样我们不仅能实现一个非const的反向迭代器,连const版本的也实现好了。
template <class Iteraior,class Ref,class Ptr>
class Reverse_iterator
{
public:
typedef Reverse_iterator<Iteraior, Ref, Ptr> self;
Reverse_iterator(const Iteraior& it)
:_it(it)
{}
self& operator++()
{
--_it;
return *this;
}
self operator++(int)
{
self tmp = *this;
--_it;
return tmp;
}
bool operator!=(const self& s)
{
return _it != s._it;
}
bool operator==(const self& s)
{
return _it == s._it;
}
Ref operator*()
{
Iteraior tmp = _it;
return *(--tmp);
}
Ptr operator->()
{
return &(*_it);
}
private:
Iteraior _it;
};
那么今天的分享就到这里了,有什么不懂得可以私信博主,或者添加博主的微信,欢迎交流。


![[自用] win 10安装cuda 10.2和cuDNN 10.2](https://img-blog.csdnimg.cn/06c8b52d91c6467ca2d8312fcc76fa83.png)