大家好，我是蓝胖子，我一直相信编程是一门实践性的技术，其中算法也不例外，初学者可能往往对它可望而不可及，觉得很难，学了又忘，忘其实是由于没有真正搞懂算法的应用场景，所以我准备出一个系列，囊括我们在日常开发中常用的算法，并结合实际的应用场景，真正的感受算法的魅力。

代码已经上传github

https://github.com/HobbyBear/codelearning/tree/master/quicksort

算法原理

快速排序的时间复杂度是O(nlgn) ，这类时间复杂度的算法逻辑(归并排序也是类似)在算法逻辑上都有个特点，一般是将整个数组一分为二，然后将分割后的数组继续一分为二，这样整个切割过程就被分成了lg n 层，然后每一层需要对数组中的元素进行操作(这个操作针对于快速排序而言就是找到基点的位置，针对于归并排序而言就是合并相邻两部分的数组)，由于每个都要对这个n个元素进行操作，所以整体的时间复杂度算下来就是O(nlgn) 。

接下来我们来仔细看下快速排序的算法逻辑，看看它是如何将数组进行切分的

下面👇🏻介绍的是三路快排的原理，相信懂了三路快排，双路快排也是很好理解的。

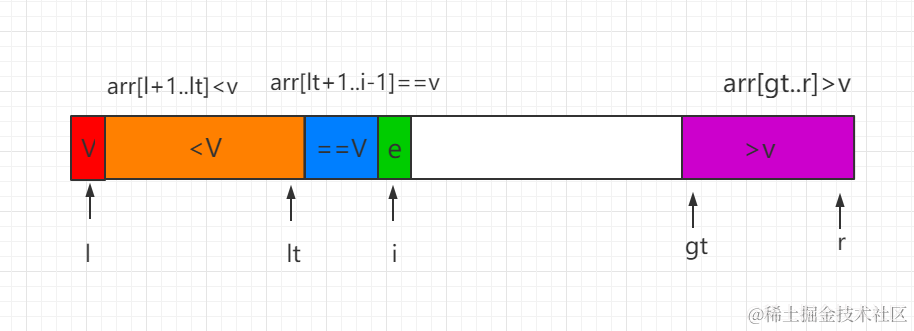
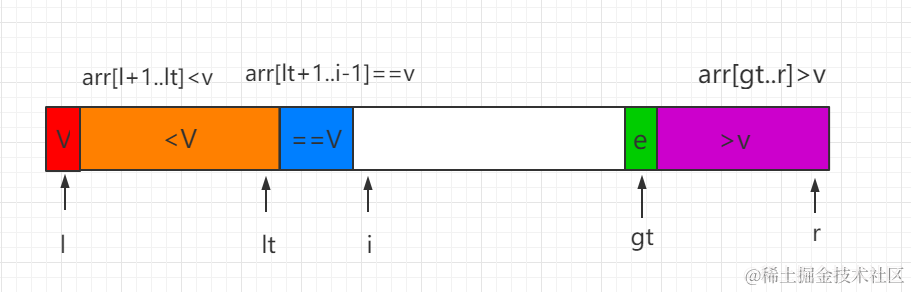
图中l代表数组的左边界，r代表数组的右边界，i代表当前遍历的元素

算法首先是在数组中选取数组首个元素作为基点，也就是图中的V，然后在遍历数组的过程中，划分出了3个空间，其中[l+1…lt] 部分会存放小于基点的元素， [gt…r] 不分在遍历完成后会存放大于基点的元素。[lt+1…gt-1]这部分区域在遍历完成后会存放等于基点的元素。在遍历完成的最后一步，则是将基点v和lt指向的元素交换位置，同时lt进行减一操作，这样最后完成遍历后，[l…lt]部分则全部放置的是小于基点的元素了。

你可以看到，在遍历完整个数组后，基点就已经找到了它在数组中应该存放的位置了，接下来就是对小于基点的部分数组，和大于基点的部分数组再次执行这个选基点分割的过程，这样每个元素便都能找到各自在数组中的正确位置。

知道了算法的大致逻辑，我们来对遍历元素过程中的三种情况进行分析，因为遍历过程中无非就是3种情况，大于V，小于V,等于V,我们应该如何移动对应的指针来让遍历完数组后，各个指针对应的区间仍然满足上面的定义就是我们需要探讨的。

小于V

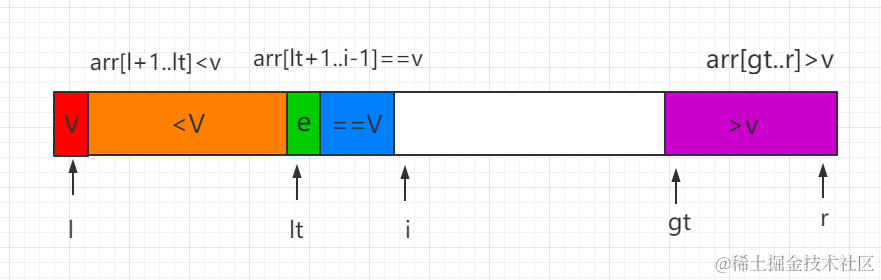
假设当前遍历到了元素e，发现 e< V ，那么就需要将e和lt+1指向的元素交换位置(lt+1位置放置的是等于V的元素)，并且更新lt指针位置到lt+1,同时需要将i进行加1操作继续遍历下一个元素。

等于V

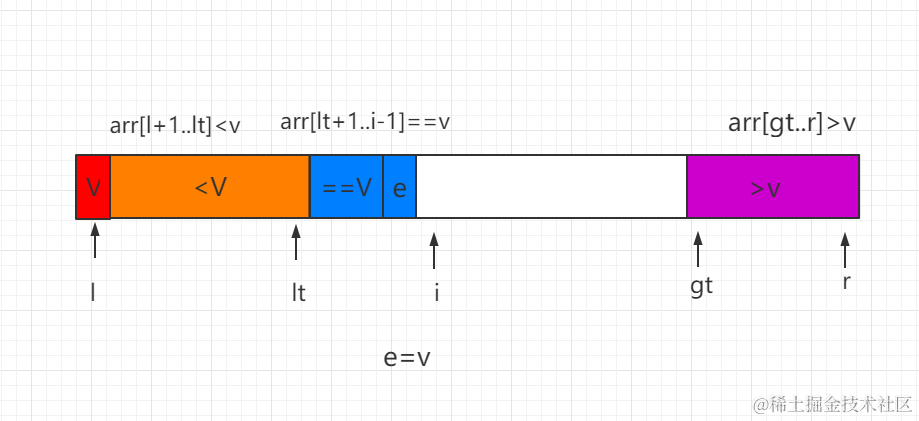
假设当前遍历到的元素是e，发现e == V ，那么只需要执行i++ ，让i继续遍历下一个元素即可。

大于V

假设当前遍历的元素e > V ，那么需要将e通gt-1位置的元素进行交换，由于交换过来的gt-1位置的元素还未遍历，所以在这一步，i不进行加1操作,gt–即可。

实现

在详细的看完快排算法的思路之后，我们用代码来实现下这部分。

很多时候写算法不能写出来，是因为你不能完整的用文字清晰的描述算法的逻辑，当你能清晰的描绘整个算法逻辑之后，写代码实现起来便是水到渠成的事。

首先，我们定义一个快排的函数，它的定义是对arr数组中的[l…r]区间内的元素进行快排。

func quickSort(arr []int, l int, r int) 

在函数内部，我们需要基点，和几个指针，lt，gt，i 它们分别对应上图中的小于V的边界，大于V的边界，当前要遍历的元素，注意我们定义的lt,gt边界都是闭区间。

在初始化边界时，大于V和小于V 的区间都是没有元素的。

lt := l     // 小于v的右边界  
gt := r + 1 // 大于v的左边界  
i := l + 1  // 当前遍历的元素
v := arr[l]  //  V 为选定的基点

剩下的就是按刚才探讨的遍历i过程对数组进行遍历，遍历的介绍条件则是i < gt 时停止遍历，完整代码如下:

func quickSort(arr []int, l int, r int) {  
   if l >= r {  
      return  
   }  
   lt := l     // 小于v的右边界  
   gt := r + 1 // 大于v的左边界  
   i := l + 1  // 当前遍历的元素  
   swap(arr, l, rand.Int()%(r-l+1)+l)  //  这一步是为了让基点随机化，否则快排在排序近乎有序数组时，不能很好达到切分数组的目的，从而让算法退化成O(n^2)的算法
   v := arr[l]  
   for i < gt {  
      if v > arr[i] {  
         tmp := arr[lt+1]  
         arr[lt+1] = arr[i]  
         arr[i] = tmp  
         lt++  
         i++  
         continue  
      }  
      if v < arr[i] {  
         gt--  
         tmp := arr[gt]  
         arr[gt] = arr[i]  
         arr[i] = tmp  
         continue  
      }  
      i++  
   }  
   tmp := arr[lt]  
   arr[lt] = v  
   arr[l] = tmp  
   lt--  
   quickSort(arr, l, lt)  
   quickSort(arr, gt, r)  
}

(应用场景)在O(n)时间复杂度内选取数组中第k大的元素

接下来，我们来看一个利用快排选取基点切分数组的思想来解决选取数组中第k大元素的问题。这是leetcode的 215号题。

215. 数组中的第K个最大元素  
中等  
2.3K  
相关企业  
给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。  
  
请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。  
  
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。  
  
示例 1:  
输入: [3,2,1,5,6,4], k = 2  
输出: 5  
示例 2:  
输入: [3,2,3,1,2,4,5,5,6], k = 4  
输出: 4  
  
提示：  
  
1 <= k <= nums.length <= 105  
-104 <= nums[i] <= 104

看完题目后，我们来回顾下快排在遍历一次数组后达到了什么效果，是找到了基点在数组中的正确位置。如果这个位置正是数组中第k大的元素，那么不就找到了这个位置吗。基于此，我们来探讨下，最后基点的位置和k的关系，注意如果数值是从大到小进行排序，那么第k大的元素索引是k-1。

和前面讲解三路快排不同，最后遍历完成后 在[l…lt]部分存放大于V的元素，在[gt…r]部分存放小于V的元素。因为我们需要从大到小排列元素。接着探讨3中情况,

基点最后的索引位置等于k-1

即 lt + 1 == k -1 ，此时我们找到了第k大的元素，可以直接返回。

基点最后索引位置 > k-1

即lt+ 1 > k -1 ,说明第k大的元素在基点的左侧，即要在[l…lt]区间继续寻找

基点最后索引位置 < k - 1

即lt + 1 < k - 1 ，说明第k的元素在基点的右侧，需要往[lt+2…r]区间进行寻找，这里还有个优化点，由于[lt+1…gt-1] 之间是存放的等于V的部分，所以如果k-1 是在[lt+1…gt-1]范围的话，还是可以直接返回基点的值，如果k-1 >= gt 的话 说明第k大的元素在 [gt…r]区间，则应该在[gt…r]区间继续寻找元素。

完整代码如下:

func findKthLargest(nums []int, k int) int {  
   return partition(nums, k, 0, len(nums)-1)  
}  
  
// 大于 v     小于v  
// v [l+1..lt]     [gt...r] 进行分区，判断 分区后的lt+1 和k的大小  
func partition(nums []int, k int, l, r int) int {  
   lt := l  
   v := nums[l]  
   gt := r + 1  
   i := l + 1 // 当前遍历元素  
   for i < gt {  
      if nums[i] < v {  
         gt--  
         swap(nums, gt, i)  
         continue  
      }  
      if nums[i] > v {  
         lt++  
         swap(nums, i, lt)  
         i++  
         continue  
      }  
      i++  
   }  
   swap(nums, l, lt)  
   lt--  
   // lt+ 1的元素处于正确位置lt+1  
   if lt+1 == k-1 {  
      return nums[lt+1]  
   }  
   if lt+1 < k-1 {  
      if gt > k-1 {  
         return nums[k-1]  
      }  
      return partition(nums, k, gt, r)  
   }  
   return partition(nums, k, l, lt)  
}