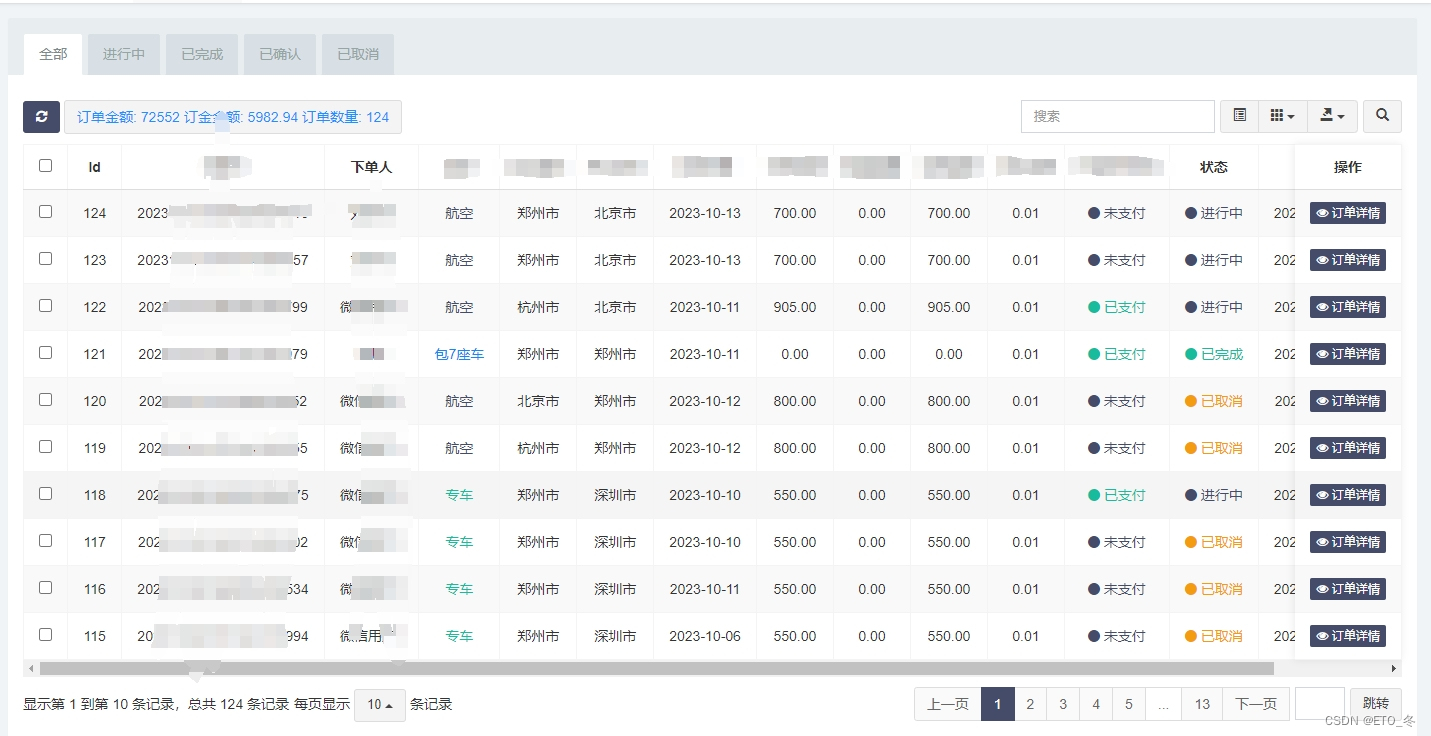
第五章 图
- 图的基本概念
- 图的应用背景
- 图的定义和术语
- 图的存储结构
- 邻接矩阵
- 邻接表
- 图的遍历
- 连通图的深度优先搜索
- 连通图的广度优先搜索
- 图的应用
- 最小生成树
- 拓扑排序
- 小试牛刀
图的基本概念
图结构中,任意两个结点之间都可能相关;而在树中,结点具有层次关系,每一层结点只能和上一层至多一个结点相关,但可能和下一层多个结点相关
图的应用背景
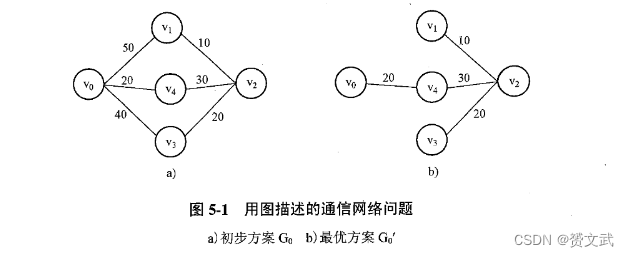
- 上图中圆圈称为顶点;连线称为边,连线附带的数值称为边的权
- 图结构可以用来描述通信网络
图的定义和术语
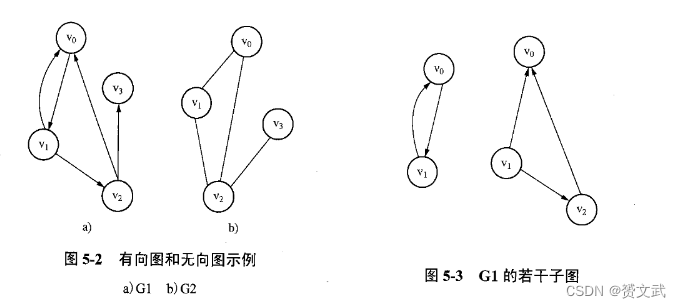
图G由两个集合V和E组成,记作G=(V,E);V是顶点的集合(有穷非空),E是边的集合
- 有向图:边是有序的(边带箭头“单行道”、用<顶点1,顶点2>表示从顶点1到顶点2的边);无向图:边是无序的(边不带箭头、用(顶点1,顶点2)表示顶点1和2之间的边)
- 弧,弧头,弧尾;弧:有向图的边称为弧;<v,w>表示从v到w的一条弧,其中v称为弧尾(或始点),w称为弧头(或终点)
任何两点之间都有边的无向图称为无向完全图;任何两点之间都有弧的有向图称为有向完全图
- 权:图的边的附带数值,实际应用中可以表示从一个顶点到另一个顶点的距离、代价或耗费等
- 带权图:每条边都带权的图称为带权图
- 顶点的度D、入度ID、出度OD:无向图中顶点的度是与该顶点相关联的边的数目,有向图中则把以顶点为终点的弧的数目称为该顶点的入度,以该顶点为始点的弧的数目称为该顶点的初读,有向图中的度为入度和出度的和
- 子图:设G=(V,E)是一个图,若E’是E的子集,V’是V的子集,并且E’中的边仅有与V’中的顶点相关联。则G’称为G的子图
- 路径、路径长度:从一个顶点到另一个顶点称为路径;路径长度就是路径(或弧)上边的数之和
- 简单路径、回路、简单回路;简单路径:序列中顶点不重复出现;第一个顶点和最后一个顶点相同的路径称为回路或环;除了第一个顶点和最后一个顶点外,其余顶点不重复的回路称为简单回路或简单环
- 连通、连通图、联通分量;连通图:在无向图中,如果从顶点v到顶点v’有路径,则称其为连通;连通图:图中任意两个顶点都是连通的;连通分量:无向图中的极大连通子图
- 强连通、强连通图、强连通分量;强连通图:有向图任意一对顶点双向连通;强连通分量:有向图的极大连通子图
- 生成树、生成森林;生成树:包含所有顶点的一个极小连通子图;生成森林:在非连通图中,每个连通分量都可得到一个极小的连通子图,即一棵生成树,这些连通分量的生成树就组成了一个非连通图的生成森林
图的存储结构
邻接矩阵
- 二维矩阵来实现,两顶点连通为1,不连通为0,行,列分别表示全部顶点,如下图所示:

注:也可用邻接矩阵表示带权图,没有边的用无穷表示,有的则用权,其余正常
邻接表
邻接表是顺序存储与链式存储相结合的存储方式

-
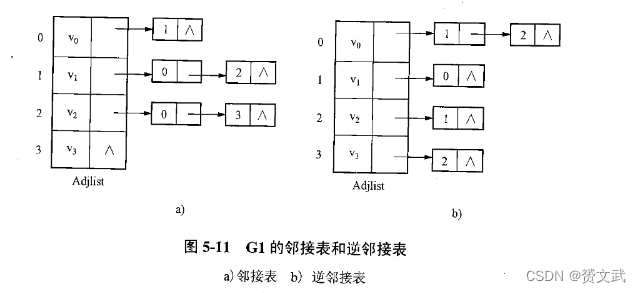
有向图的邻接表;以顶点Vi为尾的弧
-
无向图的邻接表;第i个单链表中的结点表示依赖于Vi的边
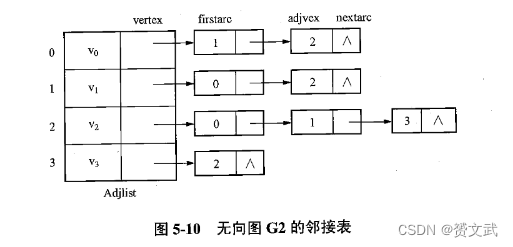
- 逆邻接表:逆邻接表是指以每个顶点作为索引,记录各个顶点的入边(即指向该顶点的边)的数据结构。(有向图的邻接表记录的是出边)
图的遍历
图的遍历是指从图的某个顶点出发,系统的访问图的每个顶点,并且每个顶点只能被访问一次
连通图的深度优先搜索
以图中某个顶点出发,首先访问出发点,然后任选一个未访问过的邻接点,以邻接点为新出发点继续,依此类推,直到所有顶点都被访问
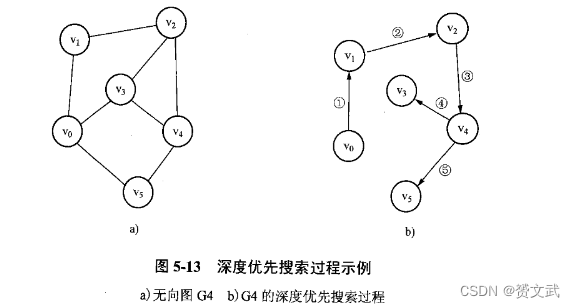
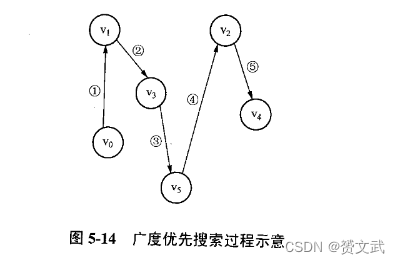
连通图的广度优先搜索
从图中某个顶点出发,访问了该顶点后依次访问该顶点的邻接点,然后从邻接点出发继续访问直到结束
图的应用
最小生成树
对于有n个顶点的无向图,所有生成树都有且仅有n-1条边
- Prim算法(假设G=(V,E)是一个带权图,生成的最小生成树为MinT=(V,T),其中V为顶点的集合,T为边的集合)
- 初始化:U={u0},T={}。其中U为一个新设置的顶点的集合,初始U中只含有顶点u0,这里假设从顶点u0出发
- 对所有u∈U,v∈V-U中,找一条权最小的边(u’,v’),将这条边加入集合T中,将顶点v’加入集合U中
- 如果U=V,则算法结束,否则重复
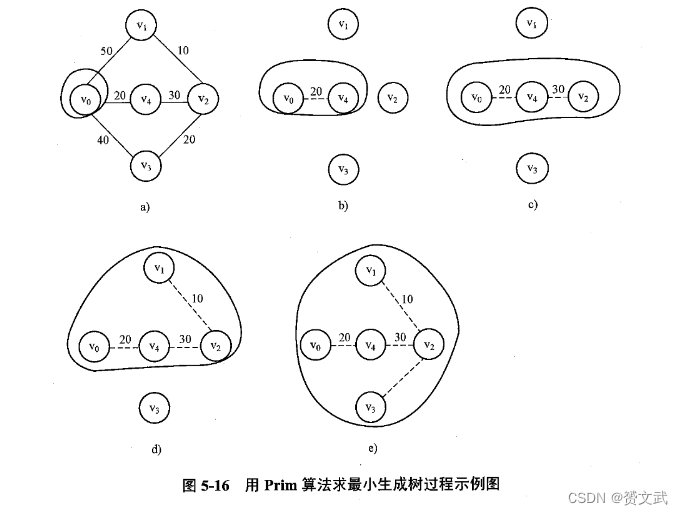
- 克鲁斯卡尔算法
- 设G=(V,E),令最小生成树初始状态为只有n个顶点而无边的非连通图T=(V,{}),每个顶点自成一个连通分量
- 在E中选取代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边,选取下一条代价最小的边
- 依此类推,直到T中所有顶点都在同一连通分量上为止
- Dijkstra求单源最短路径(设置顶点集合S,开始时S中只含有源点v)
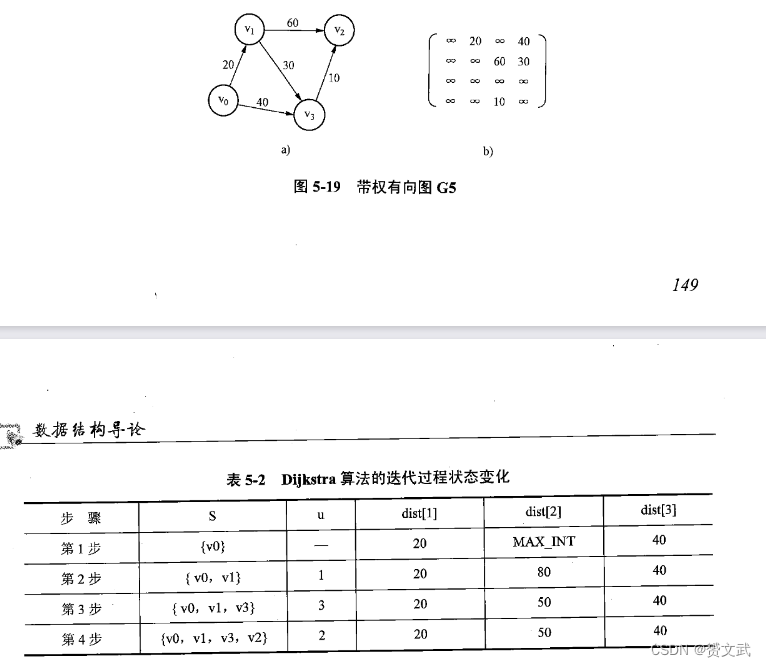
- 创建一个节点集合,初始时只包含起点节点,以及一个距离表记录起点到各个节点的当前最短距离和路径。
- 从起点开始,遍历与起点相邻的节点,并更新距离表中的距离和路径。
- 选择一个距离表中未访问过的节点中距离最短的节点,将其加入节点集合中,并继续遍历与该节点相邻的节点。若找到更短的路径,更新距离表中的距离和路径。
- 重复步骤3,直到所有节点都被加入节点集合,或者目标节点被加入节点集合。最终,距离表中记录的就是起点到各个节点的最短距离和路径。
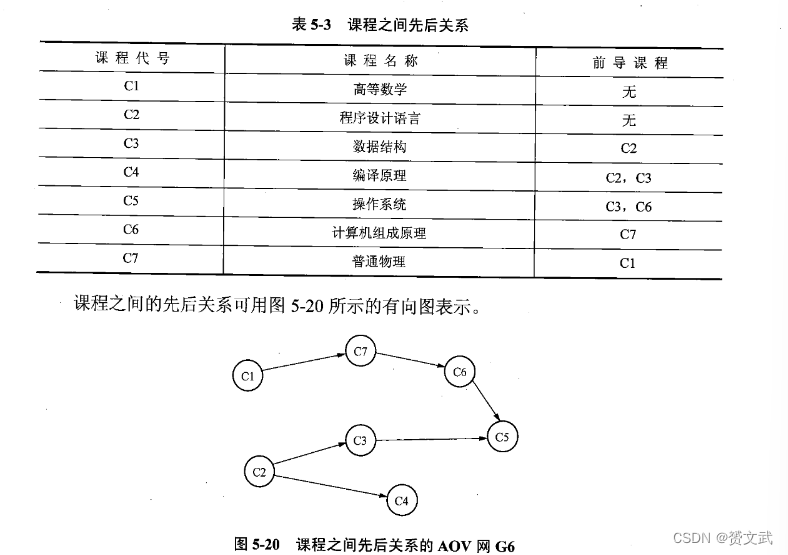
拓扑排序
- AOV网:工程或者某种流程可分为若干个小的工程或阶段,这些小的工程或阶段就称为活动;若以图中顶点表示活动,有向边表示活动之间的优先关系,这种有向图称为AOV网
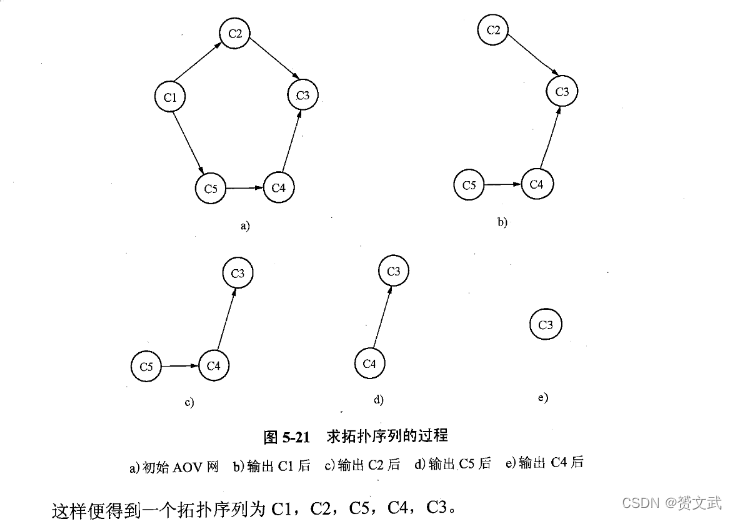
- 拓扑排序
完成拓扑排序的前提条件是AOV网中不能出现回路
有向图拓扑排序算法的基本步骤如下:
- 图中选择一个入度为0的顶点,输出该顶点
- 从图中删除该顶点及其相关联的弧,调整被删弧的弧头结点的入度(入度减1)
- 重复执行上述步骤直到所有入度为0的顶点均被输出
小试牛刀
- 一个有n个顶点的无向连通图,最少有______条边
- 无向图的邻接矩阵是_______矩阵
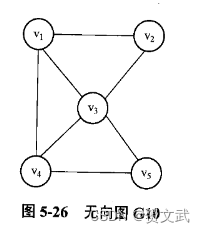
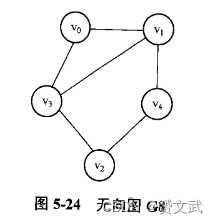
- 给出下图的邻接矩阵和邻接表
- 分别给出下图的邻接矩阵、邻接表和逆邻接表
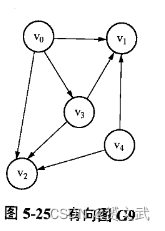
- 分别给出下图从v5出发按深度优先搜索和广度优先搜索算法遍历得到的顶点序列