题目
题有点难,但还挺有趣
有一个咖啡机数组arr[],其中arr[i]代表每一个咖啡机冲泡咖啡所需的时间,有整数N,代表着准备冲咖啡的N个人(假设这个人拿到咖啡后喝完的时间为0,拿手里咖啡杯即变空),有一台洗咖啡杯的机器,一次只能洗一只杯子,每次洗咖啡杯消耗的时间为a,如果咖啡杯自己挥发变干净,消耗的时间是b,返回从排队开始到所有咖啡杯变干净的最短时间。
分析:
- 根据题意梳理后可得知,每台咖啡机冲泡咖啡是并行操作的,但是单独的咖啡机自己,是只有等当前的咖啡冲泡完成后,才可冲泡下一杯,是串行操作的。
- 洗咖啡杯的机器消耗时间为a,但是要等咖啡冲泡完成后,才可进行清洗。举例:1号咖啡机冲泡1杯咖啡时间为2分钟,从0时间点开始冲泡一杯咖啡,2分钟时间点结束。那么洗咖啡杯的机器是在2分钟的时间点开始工作,在2 + a时间点工作完成,才可进行下一只咖啡杯的清洗。需要注意的是:如果咖啡杯1和2都选择清洗,但是1号咖啡杯是9时间点喝完,2号咖啡杯是6时间点喝完,则2号咖啡杯在清洗时,开始的时间点是 9 + a,是根据上一直需要清洗的咖啡杯的时间来决定的。
- 咖啡杯自己挥发是并行操作,并且变干净的时间都是b。
暴力递归
依然是从暴力递归开始分析,并从暴力递归转换成动态规划,但是在暴力递归之前,先将这道题拆解成2道题来看。
首先是根据咖啡机数组arr和准备冲咖啡的人数N来实现一个模拟排队的功能。作用是能够获取到每个人能够最快获取到咖啡的时间点。
模拟排队
模拟排队的功能实现用到了PriorityQueue,并且自己实现了咖啡机的比较规则,根据PriorityQueue的特性让效率最快的咖啡机始终在最上面并进行使用。其中(0,1)表示当前咖啡机可用时间点为0,冲泡一杯咖啡时间为1。
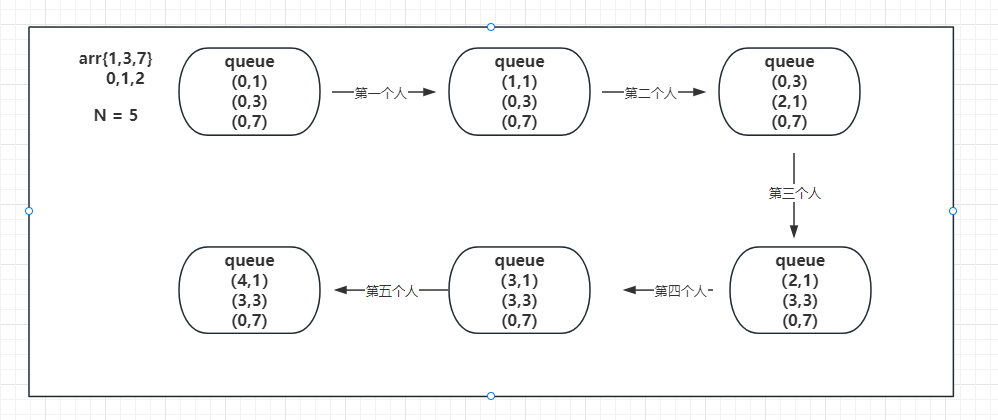
解释一下上边的图:
咖啡机数组arr{1,3,7}代表着0号咖啡机冲泡一杯咖啡所需时间为1,1号咖啡机所需时间为3,2号咖啡机所需时间为7。开始时咖啡可用时间都从0时间点开始。一共有5个人排队冲咖啡。
根据咖啡机冲泡一杯所需时间 和 咖啡机下一次可用时间 来实现咖啡机的效率最大化。
所以:
- 第一个人过来时,会去0号咖啡机冲咖啡,此时咖啡机在1时间点冲完,并且咖啡机下次可用时间点为1。
- 第二个人过来时,0号咖啡机可用时间点为1,冲泡一杯咖啡所需时间为1, 1 + 1 = 2 ,小于1号咖啡机冲泡一杯的时间3,所以还是会选择0号咖啡机冲泡咖啡。
- 第三个人过来时,0号咖啡机会在2时间点可用,冲泡一杯咖啡时间依然是1,但是此时1号咖啡机可用时间点是0,冲泡咖啡的时间是3。此时0号咖啡机和1号咖啡机冲泡一杯咖啡结束的时间点相同(用谁都可以),我们假设用1号咖啡机,用完后,1号咖啡机可用时间点为3,**根据PriorityQueue的特性,0号咖啡机又会排到上面 **。
- 所以第四个人、第五个人过来都会选择0号咖啡机。
代码
public static class Machine {
// 咖啡机可以工作的时间点
int timePoint;
//泡一杯咖啡所需时间
int workTime;
public Machine(int timePoint, int workTime) {
this.timePoint = timePoint;
this.workTime = workTime;
}
}
//自定义比较器
public static class MachineComparator implements Comparator<Machine> {
@Override
public int compare(Machine o1, Machine o2) {
return (o1.timePoint + o1.workTime) - (o2.timePoint + o2.hashCode());
}
}
public static int forceMake(int[] arr, int N, int a, int b) {
PriorityQueue<Machine> heap = new PriorityQueue<>(new MachineComparator());
//初始化时,填充heap
for (int i = 0; i < arr.length; i++) {
heap.add(new Machine(0, arr[i]));
}
//每个人最快可以喝到咖啡的数组
int[] drinks = new int[N];
for (int i = 0; i < N; i++) {
//获取堆顶的咖啡机元素
Machine curMachine = heap.poll();
//咖啡机下次可用时间
curMachine.timePoint += curMachine.workTime;
//什么时间可以喝到咖啡
drinks[i] = curMachine.timePoint;
//再次压入堆中
heap.add(curMachine);
}
//process方法是递归方法,求出咖啡杯变干净的最少时间。
return process(drinks, a, b, 0, 0);
}
第一个模拟排队的问题解决了,接下来就是正式的暴力递归。
暴力递归方法返回drinks[index…]位置变干净的最小时间。
所以此时base case也可以确定下来了 index == drinks.length。 而每只杯子可以选择清洗,也可以选择挥发变干净。
所以在递归向下传递时需要注意清洗咖啡杯机器的可用时间的变化。
代码
代码中在向下传递时,如果我选择了清洗,则机器的可用时间是会向后延长的,如果选择了风干,也是要根据咖啡杯的可用时间来取最大值的(木桶原理),最后,在清洗和风干中,取小的。
//drinks: 每个人喝到咖啡的最短时间
//wash : 用洗咖啡杯机器洗一只咖啡杯的时间
// air : 空气挥发一杯咖啡杯的时间
//index: 第几只杯子
//free : 下一次洗咖啡杯机器可用时间
public static int process(int[] drink, int wash, int air, int index, int free) {
//没有杯子了
if (index == drink.length) {
return 0;
}
//选择洗
int selfClean1 = Math.max(drink[index], free) + wash;
//向下传递,下一只杯子清洗干净的时间,此时清洗咖啡杯机器的可用时间为selfClean1
int restClean1 = process(drink, wash, air, index + 1, selfClean1);
//木桶原理,因为选择了清洗,所以要看当前杯子selfClean和下一个杯子restClean那个时间更大,选择哪个
int p1 = Math.max(selfClean1, restClean1);
// 选择风干
int selfClean2 = drink[index] + air;
//free依然是free,清洗咖啡杯机器的时间没有变化。
int restClean2 = process(drink, wash, air, index + 1, free);
//同理
int p2 = Math.max(selfClean2, restClean2);
//在风干和清洗中选择一个最小的。
return Math.min(p1, p2);
}
动态规划
根据暴力递归中的代码来改写动态规划,从暴力递归代码中可以看出,可变参数是数组下标index和清洗咖啡杯机器的freeTime。并且index的范围是 0 ~ drinks.length,需要注意的是freeTime,和之前题的可变参数范围不同。这道题中freeTime的时间范围并不好确定,需要根据具体的业务来算出来(按照drinks中最大喝完咖啡的时间 + 清洗一杯咖啡杯的时间)。
所以dp[][] 初始化时,可以确定范围 dp[N + 1][maxFree]。
还需要注意的一点是,因为在遍历dp填充值的时候,内循环是遍历maxFree,而变量free是可以无限逼近maxFree的,所以在计算restClean时,需要进行判断否则很可能会有数组下标越界的情况。
而在暴力递归过程中,无论怎么清洗咖啡杯,时间都不可能大于maxFree。所以,如果计算的selfClean1变量再加完 wash后,如果 > maxFree,则证明是无效的。在实际过程中不存在这种情况。break。这个值不用填充。
public static int dp(int[] drinks, int wash, int air) {
int N = drinks.length;
int maxFree = 0;
for (int i = 0; i < N; i++) {
maxFree = Math.max(maxFree, drinks[i]) + wash;
}
int[][] dp = new int[N + 1][maxFree + 1];
for (int index = N - 1; index >= 0; index--) {
for (int free = 0; free < maxFree; free++) {
int selfClean1 = Math.max(drinks[index], free) + wash;
if (selfClean1 > maxFree){
break;
}
int restClean1 = dp[index + 1][selfClean1];
int p1 = Math.max(selfClean1, restClean1);
int selfClean2 = drinks[index] + air;
int restClean2 = dp[index + 1][free];
int p2 = Math.max(selfClean2, restClean2);
dp[index][free] = Math.min(p1, p2);
}
}
return dp[0][0];
}
完整代码
public static class Machine {
// 咖啡机下一次可以工作的时间
int timePoint;
//泡一杯咖啡所需时间
int workTime;
public Machine(int timePoint, int workTime) {
this.timePoint = timePoint;
this.workTime = workTime;
}
}
public static class MachineComparator implements Comparator<Machine> {
@Override
public int compare(Machine o1, Machine o2) {
return (o1.timePoint + o1.workTime) - (o2.timePoint + o2.hashCode());
}
}
public static int minTime(int[] arr, int N, int a, int b) {
PriorityQueue<Machine> heap = new PriorityQueue<>(new MachineComparator());
for (int i = 0; i < arr.length; i++) {
heap.add(new Machine(0, arr[i]));
}
int[] drinks = new int[N];
for (int i = 0; i < N; i++) {
Machine curMachine = heap.poll();
drinks[i] = curMachine.timePoint;
curMachine.timePoint += curMachine.workTime;
heap.add(curMachine);
}
return process(drinks, a, b, 0, 0);
}
//drinks: 每个人喝咖啡的最短时间
//wash : 用洗咖啡杯机器洗一只咖啡杯的时间
// air : 空气挥发一杯咖啡杯的时间
//index: 第几只杯子
//free : 下一次洗咖啡杯机器可用时间
public static int process(int[] drink, int wash, int air, int index, int free) {
//没有杯子了
if (index == drink.length) {
return 0;
}
//选择洗
int selfClean1 = Math.max(drink[index], free) + wash;
int restClean1 = process(drink, wash, air, index + 1, selfClean1);
int p1 = Math.max(selfClean1, restClean1);
// 选择风干
int selfClean2 = drink[index] + air;
int restClean2 = process(drink, wash, air, index + 1, free);
int p2 = Math.max(selfClean2, restClean2);
return Math.min(p1, p2);
}
public static int minTime2(int[] arr, int N, int a, int b) {
PriorityQueue<Machine> heap = new PriorityQueue<>(new MachineComparator());
for (int i = 0; i < arr.length; i++) {
heap.add(new Machine(0, arr[i]));
}
int[] drinks = new int[N];
for (int i = 0; i < N; i++) {
Machine curMachine = heap.poll();
drinks[i] = curMachine.timePoint;
curMachine.timePoint += curMachine.workTime;
heap.add(curMachine);
}
return dp(drinks, a, b);
}
public static int dp(int[] drinks, int wash, int air) {
int N = drinks.length;
int maxFree = 0;
for (int i = 0; i < N; i++) {
maxFree = Math.max(maxFree, drinks[i]) + wash;
}
int[][] dp = new int[N + 1][maxFree + 1];
for (int index = N - 1; index >= 0; index--) {
for (int free = 0; free < maxFree; free++) {
int selfClean1 = Math.max(drinks[index], free) + wash;
if (selfClean1 > maxFree){
break;
}
int restClean1 = dp[index + 1][selfClean1];
int p1 = Math.max(selfClean1, restClean1);
int selfClean2 = drinks[index] + air;
int restClean2 = dp[index + 1][free];
int p2 = Math.max(selfClean2, restClean2);
dp[index][free] = Math.min(p1, p2);
}
}
return dp[0][0];
}


![[清华大学]漏洞挖掘之状态敏感的模糊测试StateFuzz](https://img-blog.csdnimg.cn/29d6ca316ac040faa7f3c440ec64132a.jpeg#pic_center)