论文解读：毕鑫宇

作者：Aharon Ben-Tal, Boaz Golany, Arkadi Nemirovski, Jean-Philippe Vial
引用：Ben-Tal, A., Golany, B. , Nemirovski, A., & Vial, J. P… (2005). Retailer-supplier flexible commitments contracts: a robust optimization approach. Manufacturing & Service Operations Management, 7(3), 248-271.
文章链接：https://doi.org/10.1287/msom.1050.0081

问题定义

文章研究了一个两阶段多周期供应链问题，称为零售商-供应商柔性承诺问题 (retailer-supplier flexible commitment，RSFC).

"零售商-供应商柔性承诺问题"是一个供应链管理的概念，涉及到供应商和零售商之间的合同安排。它主要关注如何灵活地承诺产品或服务的供应，以应对市场需求的不确定性。在这种情况下，"柔性承诺"通常是指供应商对零售商做出的灵活供应承诺，即供应商将根据市场条件的变化和/或零售商的需求来调整产品或服务的供应量。这种灵活性可以帮助供应链更好地应对市场的波动和不确定性，例如季节性的需求变化或突发事件导致的需求激增.然而，这种柔性承诺也会带来一些挑战，包括：

1. 需求预测：供应商需要准确地预测未来的需求以准备适当的供应量;
2. 生产和库存管理：供应商需要灵活地管理生产和库存以满足不断变化的需求;
3. 合同设计：供应商和零售商需要设计一种合同，可以公平地分享柔性承诺带来的收益和风险。

文章所关注的RSFC问题具有不确定需求，且已知只存在某不确定集中。具体而言，此问题涉及一家零售商，该零售商面临终端客户对产品的不确定需求。 零售商从供应商处订购并根据合同进行运营，根据该合同，零售商承诺（在时间为零时）固定时间范围内的订单数量向量，然后动态地用实际订单替换这些承诺的数量。 除了通常的成本（订购、持有和短缺）和最终残值之外，零售商还会因实际订单与承诺订单之间的偏差以及连续承诺/实际订单之间的偏差而受到处罚而产生额外成本。

作者采用最小-最大 (min-max) 准则，即解决 min-max RSFC 问题。为解决大规模复杂系统问题，文章采用适用于动态决策问题的鲁棒优化方法的扩展，即仿射可调鲁棒对等方法 (affinely adjustable robust counterpart，AARC), 详见 Ben-Tal et al. (2004).

AARC 的一个主要特点是在了解部分不确定数据后，可以确定部分决策变量。 在 AARC 方法中，这些“可调整”变量对已实现数据的依赖性仅限于仿射函数的形式，因而实现易处理性。 事实上，在 AARC 方法中，一系列不确定的线性规划被单个易处理的确定性问题（线性或二次曲线问题）所取代。 当然，仅使用次优策略所付出的代价是因具体问题而异的，但对于文章讨论的问题，作者通过大型模拟研究，表明该代价非常低。

模型构建

文章考虑一个单产品、两阶段 (echelon)、$T$周期、定期管理库存的问题。在计划范围的开始，零售商为产品指定承诺向量$w=w_1,\dots ,w_T$, 作为供应商对其生产能力的预测。在每个时期 $t$开始时，零售商初始库存为$x_t$，且以单位成本$c_t$从供应商处订购数量$q_t$, 随后收到顾客需求。零售商在计划范围开始时的状态通过参数$x_1$（初始库存）和$w_0$（一个名义值，可能表示计划范围之前的最后一个订单或以前订单的平均值）给出。因此，产生了以下成本:

1. 持有成本$=h_t\max [x_t+q_t-d_t,0]$，其中$h_t$为单位持有成本，
2. 缺货成本$=p_t\max [d_t-x_t-q_t,0]$，其中$p_t$为单位缺货成本。
   此外，由于合同的规定，零售商产生了以下额外费用:
3. 由于承诺订单和实际订单之间的偏差而造成的惩罚成本（可理解为“预测误差”）
   $${\alpha }_t^{+}max[q_t-w_t,0]+{\alpha }_t^{-}max[w_t-q_t,0],$$
   其中${\alpha }_t^{+},{\alpha }_t^{-}$分别为正偏差和负偏差的单位惩罚成本；
4. 对连续承诺之间偏差的惩罚成本
   $${\beta }_t^{+}max[w_t-w_{t-1},0]+{\beta }_t^{-}max[w_{t-1}-w_t,0],$$
   其中${\beta }_t^{+},{\beta }_t^{-}$是相关的单位惩罚。

同时，计划期末的剩余存货$x_{T+1}$存在单位残值为$s$, 且要求为了在文章的上下文中有意义，$s<c_T$. 且为保持模型中目标函数的凸性，$s$必须在终端周期$T$满足不等式
$$h_T-s\ge -p_T$$

模型中的约束包括：

1. 库存平衡: $x_{t+1}=x_t+q_t-d_t$;
2. 每个时期订购量的上下界: $L_t\le -q_t\le U_t$;
3. 每个时期累计订购量的上下界: ${\hat{L}}_t\le {\sum }_{\tau =1}^t{q}_{\tau }\le {\hat{U}}_t$.

后两类约束条件中参数$(L_t,U_t,{\hat{L}}_t,{\hat{U}}_t)$赋值的选择为零售商和供应商之间的各种契约协议提供了柔性模型的灵活性。

---

如果模型的所有参数都已知，包括需求向量$d=(d_1,\dots ,d_T)$，则 RSFC 问题用以下确定性数学规划表示(其中$[\xi {]}^{+}\equiv \max [\xi ,0]$)：

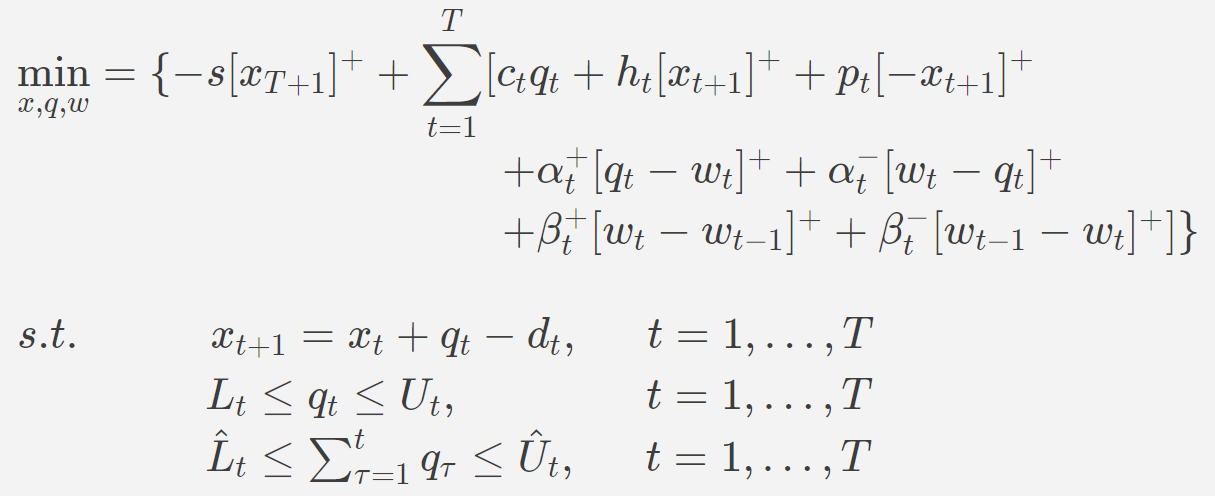
AARC方法

RSFC问题，像许多其他的OM问题一样，是一个一般的不确定T-时期LP问题的实例，它的数据$\{(A_t,c_t,b_t):$
$t=1,2,\dots ,T\}$仿射性依赖于不确定参数$\lambda =（{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_T)$的向量:
min ⁡ x = x 1 , … , x T { ∑ t = 1 T c t ( λ ) x t : ∑ τ = 1 t x τ A t τ ( λ ) ≤ b t ( λ ) , t = 1 , 2 , … , T } \displaystyle\min_{x=x_1,\ldots,x_T}\{\sum_{t=1}^Tc_t(\lambda)x_t:\sum_{\tau=1}^tx_\tau A_t^\tau(\lambda)\leq b_t(\lambda),t=1,2,\ldots,T\} x=x1​,…,xT​min​{t=1∑T​ct​(λ)xt​:τ=1∑t​xτ​Atτ​(λ)≤bt​(λ),t=1,2,…,T}

其中$A_t^{\tau },b_t$是相同维数的向量。

将向量$x$划分为$x=(x^a,x^{na})$。其中子向量量$x^{na}$(不可调变量)由“here and now”决策组成，即必须在任何不确定数据实现之前确定的决策。（在RSFC问题中，它们是:量$q_1$-第一时期的订购量，以及承诺量$w_1,w_2,\dots ,w_T$.）子向量量$x^a$(可调变量)由“wait and see”决策组成，这些决策可以在必须做出决策时根据所显示的数据进行调整（在RSFC问题中，$x^a=（q_2,\dots ,q_T)$）。

$x=(x^a,x^{na})$的划分会导致索引集 { 1 , 2 , … , T } = I a ∪ I n a \{1,2,\ldots,T\}=I_a\cup I_{na} {1,2,…,T}=Ia​∪Ina​的划分，根据这个划分，我们现在可以对时间相关(多周期)不确定LP进行如下建模:

最小-最大多周期可调鲁棒对等（Adjustable Robust Counterpart，ARC）

min ⁡ x n a , E { E : s u c h t h a t ∀ λ ∈ Λ ∃ x t = x t ( λ t − 1 ) , t ∈ I a : \displaystyle\min_{x_{na},E}\{E:such that \forall\lambda \in\Lambda \exists x_t=x_t(\lambda^{t-1}),t\in I_a: xna​,Emin​{E:suchthat∀λ∈Λ∃xt​=xt​(λt−1),t∈Ia​:
$$\sum _{\tau \in I_{na}}{c}_{\tau }(\lambda )x_{\tau }+\sum _{\tau \in I_a}{c}_{\tau }(\lambda )x_{\tau }({\lambda }^{\tau -1})\le E,$$
$$\sum _{\tau \in I_{na}(t)}{x}_{\tau }{A}_t^{\tau }(\lambda )+\sum _{\tau \in I_a(t)}{x}_{\tau }({\lambda }^{t-1})A_t^{\tau }(\lambda )\le b_t(\lambda ),$$
$$t=1,\dots ,T\}$$
其中${\lambda }^s=({\lambda }_1,\dots ,{\lambda }_s)$， I n a ( t ) = I n a ∩ { 1 , … , t } , I a ( t ) = I a ∩ { 1 , … , t } I_{na}(t)=I_{na}\cap \{1,\ldots,t\},I_a(t)=I_{a}\cap\{1,\ldots,t\} Ina​(t)=Ina​∩{1,…,t},Ia​(t)=Ia​∩{1,…,t}.

ARC模型提供的额外灵活性被它通常在计算上难以处理（NP-hard）的事实所抵消。即使对于简单的不确定性集（例如，一般多面体集）也是如此。求解ARC模型的核心难点在于$x_t^a$与“历史” ${\lambda }^{t-1}$之间未知的的函数关系。为了克服这一困难，Ben-Tal等人（2004）建议通过将这些函数关系限制为仿射来近似ARC解。因此，将ARC模型中的每个可调变量$x_t^a$通过以下线性决策规则( linear decision rule，LDR)替换为:
$$x_t^a({\lambda }^{t-1})={\mu }_t^0+\sum _{\tau =1}^{t-1}{\mu }_t^{\tau }{\lambda }_{\tau }$$

其中系数${\mu }_t^{\tau }$是新的决策变量。注意，只有当向量${\lambda }^{t-1}$在时期$t$实现时，策略$x_t^a({\lambda }^{t-1})$的实际值才由上述LDR规则决定。于是通过上述的仿射变换，ARC模型通过仿射可调RC（AARC）模型进行近似:

E ∗ ∗ = min ⁡ x n a , E , μ s τ { E : ∀ λ ∈ Λ : ∑ τ ∈ I n a c τ ( λ ) x τ + ∑ τ ∈ I a c τ ( λ ) [ μ τ 0 + ∑ s = 1 τ − 1 μ τ s λ s ] ≤ E , E^{**}=\displaystyle\min_{x_{na},E,\mu_s^\tau}\{E:\forall\lambda \in\Lambda:\sum_{\tau \in I_{na}}c_\tau(\lambda)x_\tau+\sum_{\tau \in I_{a}}c_\tau(\lambda)[ \mu _\tau^0+\sum_{s=1}^{\tau-1}\mu _\tau^s\lambda_s]\leq E, E∗∗=xna​,E,μsτ​min​{E:∀λ∈Λ:τ∈Ina​∑​cτ​(λ)xτ​+τ∈Ia​∑​cτ​(λ)[μτ0​+s=1∑τ−1​μτs​λs​]≤E,
$$\sum _{\tau \in I_{na}(t)}{x}_{\tau }{A}_t^{\tau }(\lambda )+\sum _{\tau \in I_a(t)}[{\mu }_{\tau }^0+\sum _{s=1}^{\tau -1}{\mu }_{\tau }^s{\lambda }_s]A_t^{\tau }(\lambda )\le b_t(\lambda ),$$
$$t=1,\dots ,T\}.$$

与LP RSFC问题对应的AARC模型

$$\underset{q_t^{\tau },x_{t+1}^{\tau },y_t^{\tau },u_t^{\tau },w_t,z_t,E}{\min }E$$
$$s.t.E\ge \sum _{t=1}^T[c_t{q}_t^0+y_t^0+u_t^0+z_t+\sum _{\tau =1}^{t-1}[c_t{q}_t^{\tau }+y_t^{\tau }+u_t^{\tau }]d_{\tau }]$$
$$\forall d\in u_{\ell }\text{and}\forall t=1,\dots ,T,$$
$$(x^{\ast })x_{t+1}^0\sum _{\tau =1}^t{x}_{t+1}^{\tau }{d}_{\tau }=x_t^0+\sum _{\tau =1}^{t-1}{x}_t^{\tau }{d}_{\tau }+q_t^0+\sum _{\tau =1}^{t-1}{q}_t^{\tau }{d}_{\tau }-d_t,$$
$$y_t^0+\sum _{\tau =1}^{t-1}{y}_t^{\tau }{d}_{\tau }\ge {\overline{h}}_t[x_{t+1}^0+\sum _{\tau =1}^{t-1}{x}_{t+1}^{\tau }{d}_{\tau }],\forall d\in u_{box},$$
$$y_t^0+\sum _{\tau =1}^{t-1}{y}_t^{\tau }{d}_{\tau }\ge -p_t[x_{t+1}^0+\sum _{\tau =1}^{t-1}{x}_{t+1}^{\tau }{d}_{\tau }],\forall d\in u_{box},$$
$$u_t^0+\sum _{\tau =1}^{t-1}{u}_t^{\tau }{d}_{\tau }\ge {\alpha }_t^{+}[q_t^0+\sum _{\tau =1}^{t-1}{q}_t^{\tau }{d}_{\tau }-w_{]},\forall d\in u_{box},$$ >$$u_t^0+\sum _{\tau =1}^{t-1}{u}_t^{\tau }{d}_{\tau }\ge -{\alpha }_t^{-}[q_t^0+\sum _{\tau =1}^{t-1}{q}_t^{\tau }{d}_{\tau }-w_{]},\forall d\in u_{box},$$
$$z_t\ge {\beta }_t^{+}(w_t-w_{t-1}),$$
$$z_t\ge -{\beta }_t^{-}(w_t-w_{t-1}),$$
$$L_t\le q_t^0+\sum _{\tau =1}^{t-1}{q}_t^{\tau }{d}_{\tau }\le U_t,\forall d\in u_{box},$$
$${\hat{L}}_t\le \sum _{\tau =1}^t(q_{\tau }^0+\sum _{\theta =1}^{\tau -1}{q}_{\tau }^{\theta }{d}_{\theta }\le {\hat{U}}_t,\forall d\in u_{box},$$
$$q_t^{\tau },(t,\tau )\in J_t.$$
该模型的具体推导详看原文的第二节和第三节。

优势

文章进行的分析表明，在AARC问题中的每一个半无限约束都可以等效地写成一组有限的线性约束或一个单一的二次约束。这些约束类型的问题被称为二次型（conic-quadratic，CQ）。众所周知，它们是多项式可解的(参见，例如，Ben-Tal和Nemirovski，2001)，并且可以使用非常有效的算法（和软件，例如，MOSEK）来找到它们的解。特别地，如果所有的不确定性集都是类型为box(或者，更一般地，多面体集)，则AARC是LP问题。

讨论

与其他方法一样，AARC 也有一定的局限性。
目前，其只适用于确定性线性多阶段有限周期的问题，并且只适用于不确定性是外生给定而非受内生决策变量影响的问题。例如，它不适用于今天选择的市场价格会影响明天需求的不确定性的多阶段定价问题。
AARC 方法使用最小目标函数，如果没有关于不确定参数概率分布的可靠知识，这种方法是合理的。否则，基于期望值、中位数等的目标函数可能更合适，并会导致政策不那么保守。不过，我们认为，即使在后一种情况下，如果决策者希望其所选政策在面对不确定性时的表现能得到有力的保证，也可以采用最小最大法。
最后，AARC 使用线性决策规则来获得近似解，因此无法保证最优解（通常不可能找到）接近线性决策规则。

参考文献

Ben-Tal, A., A. Goryashko, E. Guslitzer, A. Nemirovski. 2004.Adjusting robust solutions of uncertain linear programs. Math.Programming 99(2) 351–376.

Ben-Tal, A., A. Nemirovski. 2001. Lectures on Modern Convex Optimization: Analysis, Algorithms and Engineering Applications.SIAM-MPS Series in Optimization. SIAM, Philadelphia, PA.