本文全面深入地探讨了梯度下降及其变体——批量梯度下降、随机梯度下降和小批量梯度下降的原理和应用。通过数学表达式和基于PyTorch的代码示例，本文旨在为读者提供一种直观且实用的视角，以理解这些优化算法的工作原理和应用场景。

关注TechLead，分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验，同济本复旦硕，复旦机器人智能实验室成员，阿里云认证的资深架构师，项目管理专业人士，上亿营收AI产品研发负责人。

一、简介

梯度下降（Gradient Descent）是一种在机器学习和深度学习中广泛应用的优化算法。该算法的核心思想非常直观：找到一个函数的局部最小值（或最大值）通过不断地沿着该函数的梯度（gradient）方向更新参数。

什么是梯度下降？

简单地说，梯度下降是一个用于找到函数最小值的迭代算法。在机器学习中，这个“函数”通常是损失函数（Loss Function），该函数衡量模型预测与实际标签之间的误差。通过最小化这个损失函数，模型可以“学习”到从输入数据到输出标签之间的映射关系。

为什么梯度下降重要？

1. 广泛应用：从简单的线性回归到复杂的深度神经网络，梯度下降都发挥着至关重要的作用。

2. 解决不可解析问题：对于很多复杂的问题，我们往往无法找到解析解（analytical solution），而梯度下降提供了一种有效的数值方法。

3. 扩展性：梯度下降算法可以很好地适应大规模数据集和高维参数空间。

4. 灵活性与多样性：梯度下降有多种变体，如批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）和小批量梯度下降（Mini-batch Gradient Descent），各自有其优点和适用场景。

---

二、梯度下降的数学原理

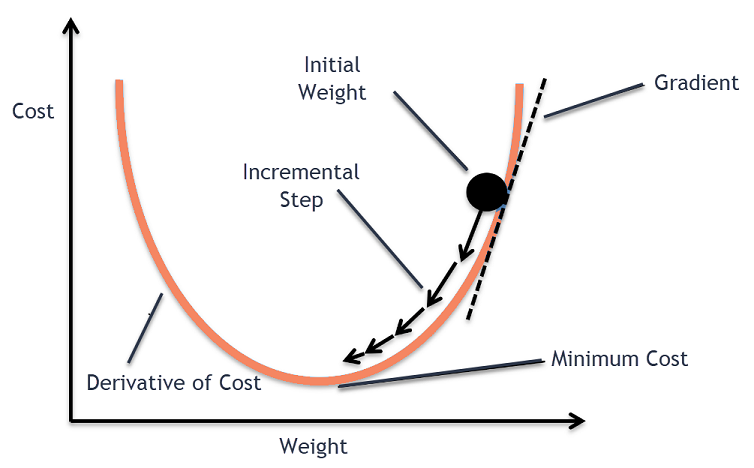
在深入研究梯度下降的各种实现之前，了解其数学背景是非常有用的。这有助于更全面地理解算法的工作原理和如何选择合适的算法变体。

代价函数（Cost Function）

在机器学习中，代价函数（也称为损失函数，Loss Function）是一个用于衡量模型预测与实际标签（或目标）之间差异的函数。通常用 ( J(\theta) ) 来表示，其中 ( \theta ) 是模型的参数。

梯度（Gradient）

更新规则

代码示例：基础的梯度下降更新规则

import numpy as np

def gradient_descent_update(theta, grad, alpha):
    """
    Perform a single gradient descent update.
    
    Parameters:
    theta (ndarray): Current parameter values.
    grad (ndarray): Gradient of the cost function at current parameters.
    alpha (float): Learning rate.
    
    Returns:
    ndarray: Updated parameter values.
    """
    return theta - alpha * grad

# Initialize parameters
theta = np.array([1.0, 2.0])
# Hypothetical gradient (for demonstration)
grad = np.array([0.5, 1.0])
# Learning rate
alpha = 0.01

# Perform a single update
theta_new = gradient_descent_update(theta, grad, alpha)
print("Updated theta:", theta_new)

输出：

Updated theta: [0.995 1.99 ]

在接下来的部分，我们将探讨梯度下降的几种不同变体，包括批量梯度下降、随机梯度下降和小批量梯度下降，以及一些高级的优化技巧。通过这些内容，你将能更全面地理解梯度下降的应用和局限性。

---

三、批量梯度下降（Batch Gradient Descent）

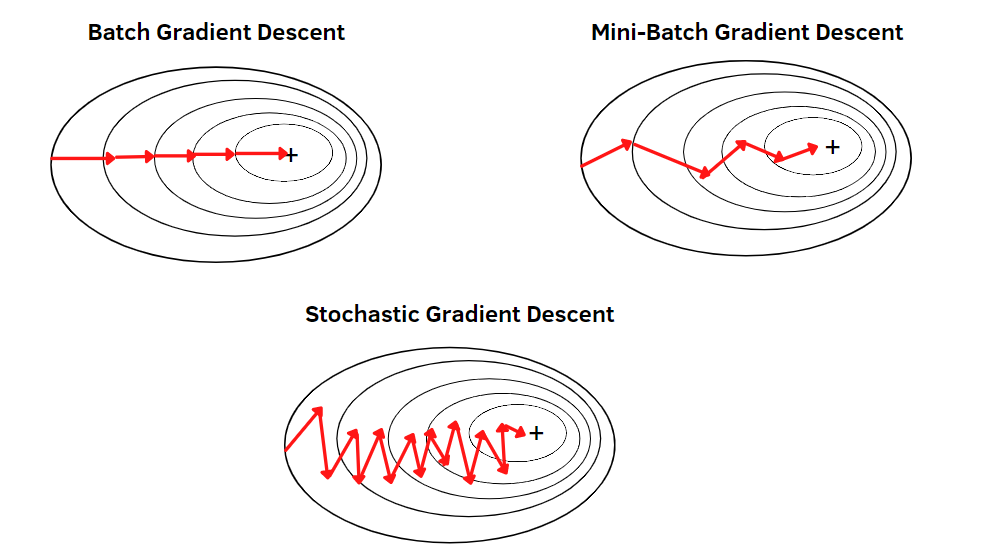
批量梯度下降（Batch Gradient Descent）是梯度下降算法的一种基础形式。在这种方法中，我们使用整个数据集来计算梯度，并更新模型参数。

基础算法

批量梯度下降的基础算法可以概括为以下几个步骤：

代码示例

下面的Python代码使用PyTorch库演示了批量梯度下降的基础实现。

import torch

# Hypothetical data (features and labels)
X = torch.tensor([[1.0, 2.0], [2.0, 3.0], [3.0, 4.0]], requires_grad=True)
y = torch.tensor([[1.0], [2.0], [3.0]])

# Initialize parameters
theta = torch.tensor([[0.0], [0.0]], requires_grad=True)

# Learning rate
alpha = 0.01

# Number of iterations
n_iter = 1000

# Cost function: Mean Squared Error
def cost_function(X, y, theta):
    m = len(y)
    predictions = X @ theta
    return (1 / (2 * m)) * torch.sum((predictions - y) ** 2)

# Gradient Descent
for i in range(n_iter):
    J = cost_function(X, y, theta)
    J.backward()
    with torch.no_grad():
        theta -= alpha * theta.grad
    theta.grad.zero_()

print("Optimized theta:", theta)

输出：

Optimized theta: tensor([[0.5780],
        [0.7721]], requires_grad=True)

批量梯度下降的主要优点是它的稳定性和准确性，但缺点是当数据集非常大时，计算整体梯度可能非常耗时。接下来的章节中，我们将探索一些用于解决这一问题的变体和优化方法。

---

四、随机梯度下降（Stochastic Gradient Descent）

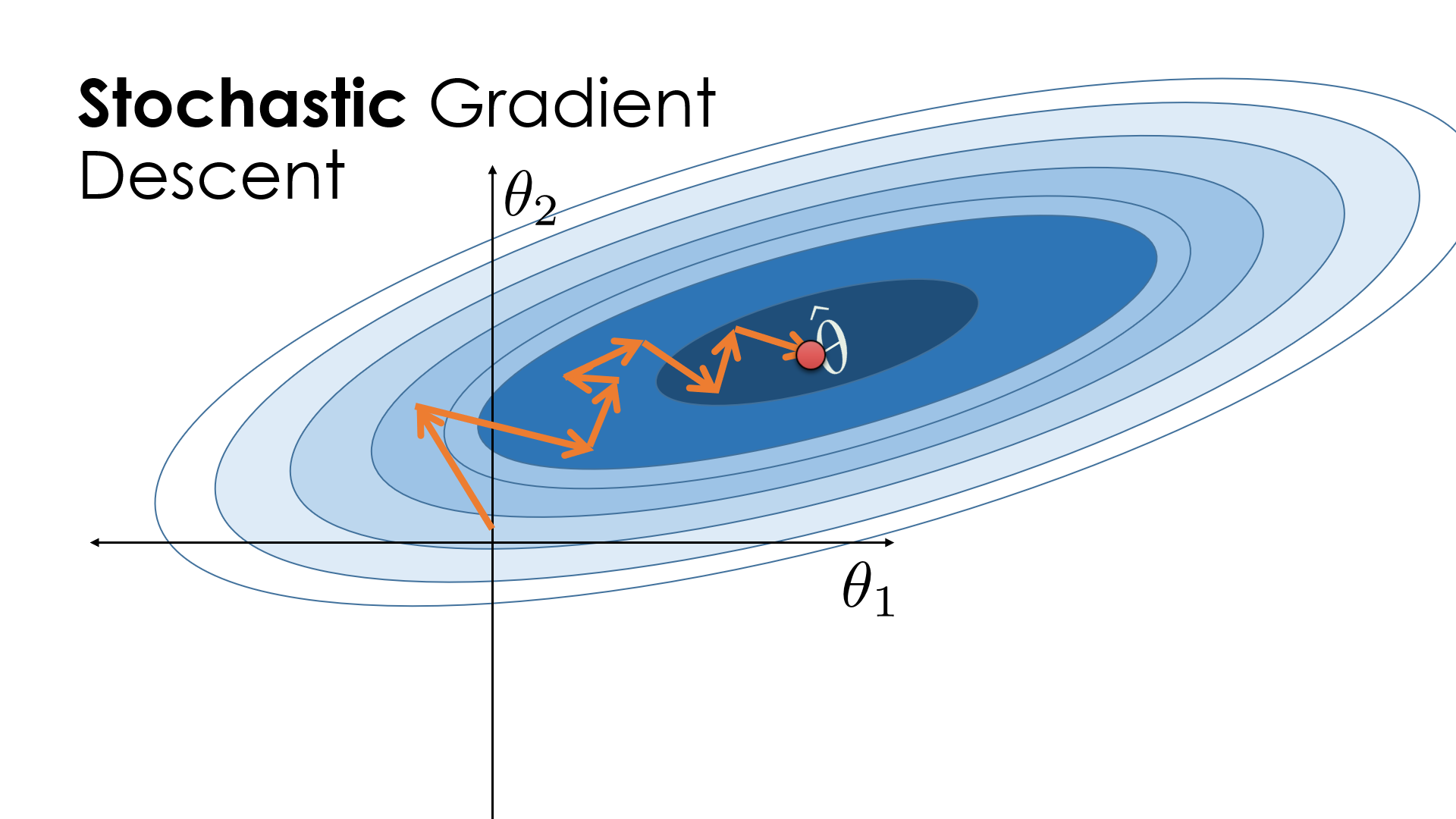
随机梯度下降（Stochastic Gradient Descent，简称SGD）是梯度下降的一种变体，主要用于解决批量梯度下降在大数据集上的计算瓶颈问题。与批量梯度下降使用整个数据集计算梯度不同，SGD每次只使用一个随机选择的样本来进行梯度计算和参数更新。

基础算法

随机梯度下降的基本步骤如下：

代码示例

下面的Python代码使用PyTorch库演示了SGD的基础实现。

import torch
import random

# Hypothetical data (features and labels)
X = torch.tensor([[1.0, 2.0], [2.0, 3.0], [3.0, 4.0]], requires_grad=True)
y = torch.tensor([[1.0], [2.0], [3.0]])

# Initialize parameters
theta = torch.tensor([[0.0], [0.0]], requires_grad=True)

# Learning rate
alpha = 0.01

# Number of iterations
n_iter = 1000

# Stochastic Gradient Descent
for i in range(n_iter):
    # Randomly sample a data point
    idx = random.randint(0, len(y) - 1)
    x_i = X[idx]
    y_i = y[idx]

    # Compute cost for the sampled point
    J = (1 / 2) * torch.sum((x_i @ theta - y_i) ** 2)
    
    # Compute gradient
    J.backward()

    # Update parameters
    with torch.no_grad():
        theta -= alpha * theta.grad

    # Reset gradients
    theta.grad.zero_()

print("Optimized theta:", theta)

输出：

Optimized theta: tensor([[0.5931],
        [0.7819]], requires_grad=True)

优缺点

SGD虽然解决了批量梯度下降在大数据集上的计算问题，但因为每次只使用一个样本来更新模型，所以其路径通常比较“嘈杂”或“不稳定”。这既是优点也是缺点：不稳定性可能帮助算法跳出局部最优解，但也可能使得收敛速度减慢。

在接下来的部分，我们将介绍一种折衷方案——小批量梯度下降，它试图结合批量梯度下降和随机梯度下降的优点。

---

五、小批量梯度下降（Mini-batch Gradient Descent）

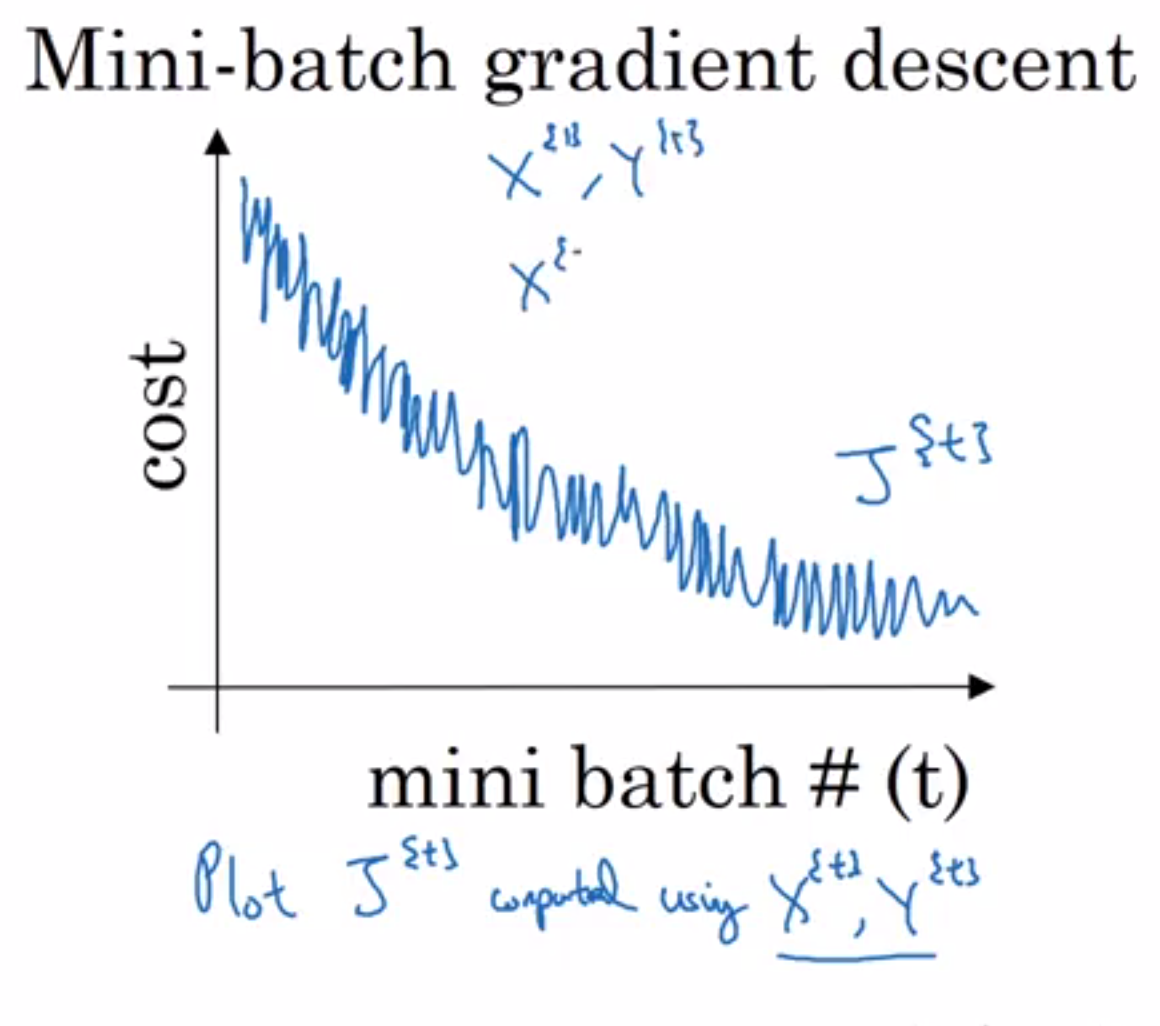
小批量梯度下降（Mini-batch Gradient Descent）是批量梯度下降和随机梯度下降（SGD）之间的一种折衷方法。在这种方法中，我们不是使用整个数据集，也不是使用单个样本，而是使用一个小批量（mini-batch）的样本来进行梯度的计算和参数更新。

基础算法

小批量梯度下降的基本算法步骤如下：

代码示例

下面的Python代码使用PyTorch库演示了小批量梯度下降的基础实现。

import torch
from torch.utils.data import DataLoader, TensorDataset

# Hypothetical data (features and labels)
X = torch.tensor([[1.0, 2.0], [2.0, 3.0], [3.0, 4.0], [4.0, 5.0]], requires_grad=True)
y = torch.tensor([[1.0], [2.0], [3.0], [4.0]])

# Initialize parameters
theta = torch.tensor([[0.0], [0.0]], requires_grad=True)

# Learning rate and batch size
alpha = 0.01
batch_size = 2

# Prepare DataLoader
dataset = TensorDataset(X, y)
data_loader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

# Mini-batch Gradient Descent
for epoch in range(100):
    for X_batch, y_batch in data_loader:
        J = (1 / (2 * batch_size)) * torch.sum((X_batch @ theta - y_batch) ** 2)
        J.backward()
        with torch.no_grad():
            theta -= alpha * theta.grad
        theta.grad.zero_()

print("Optimized theta:", theta)

输出：

Optimized theta: tensor([[0.6101],
        [0.7929]], requires_grad=True)

优缺点

小批量梯度下降结合了批量梯度下降和SGD的优点：它比SGD更稳定，同时比批量梯度下降更快。这种方法广泛应用于深度学习和其他机器学习算法中。

小批量梯度下降不是没有缺点的。选择合适的批量大小可能是一个挑战，而且有时需要通过实验来确定。

关注TechLead，分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验，同济本复旦硕，复旦机器人智能实验室成员，阿里云认证的资深架构师，项目管理专业人士，上亿营收AI产品研发负责人。