文章目录
- 一、背景
- 二、方法
- 2.1 神经辐射场场景表达
- 3.2 使用辐射场来进行立体重建
- 3.3 优化神经辐射场
- 3.3.1 位置编码
- 3.3.2 分层立体采样
- 3.3.3 具体实现细节
- 三、效果
论文:Representing Scenes as Neural Radiance Fields for View Synthesis
代码:https://github.com/bmild/nerf
官网:https://www.matthewtancik.com/nerf
一、背景
什么是神经辐射场:
- 全连接网络
- 输入为 5D coordinate:空间位置 ( x , y , z ) (x,y,z) (x,y,z),视觉方向 ( θ , ϕ ) (\theta, \phi) (θ,ϕ)
- 输出:从输入的位置和方向看过去的位置的颜色(view-dependent emitted radiance)和透明度(volume density),每个位置的透明度就控制了光线穿过该位置时的通过率
- 如何使用输出:根据输出的颜色和透明度,使用渲染的方法来将其映射到图像中
在本文中,作者为了解决视觉合成任务中一个存在已久的问题,直接优化 5D 输入参数来最小化渲染图像和真实图像的误差
这里,作者是这样使用一个 5D 函数表达一个静态场景的:
- 空间位置 ( x , y , z ) (x,y,z) (x,y,z)
- 视觉方向 ( θ , ϕ ) (\theta, \phi) (θ,ϕ)
方向被视为 2D 的是因为它通常由两个角度参数(例如,方位角和仰角)来定义。这两个参数足以描述空间中任何一个方向。
- 具体来说,在立体几何中,我们可以使用球坐标系统来描述一个点的位置。
- 在球坐标系统中,一个点的位置由三个参数确定:半径、仰角和方位角。然而,在NeRF模型中,我们假定光线从相机出发并穿过像素网格,并且所有光线都有相同的起始点(也就是相机焦点)。因此,“半径”对于描述光线路径没有意义,在这种情况下只需要两个角度参数就足以描述光线路径了
- 方位角 (Azimuthal Angle):在球坐标系中,方位角通常表示从某个参考线(如正北或正东)开始到投影点与参考线之间的水平夹角。这个角度通常在0°到360°之间变化。
- 仰角 (Elevation Angle):也被称为天顶距离,它表示从地平线(对于地球)或者水平面(对于一般情况)上升到目标方向的垂直夹角。这个夹角通常定义范围是-90°到90°,其中0°表示目标处于水平面上,+90°表示目标正好在你头顶上方(也就是天顶),-90°则代表目标正好在你脚下。
这里的神经辐射场是什么样的呢:
- 多层类似 MLP 的全连接网络
- 输入为 5D coordinate: ( x , y , z , θ , ϕ ) ) (x,y,z,\theta, \phi)) (x,y,z,θ,ϕ))
- 输出为对应位置的透明度和 RGB 颜色

怎样才能将神经辐射场的输出渲染成对应视角的图像呢:
- 首先,需要通过场景投射相机光线,生成一组采样的 3D 点
- 然后,使用这些点及其对应的 2D 观察方向作为神经网络的输入,以产生一组输出颜色和密度
- 接着, 使用经典的体积渲染技术将这些颜色和透明度累积成一个 2D 图像。因为这个过程是自然可微分的,可以使用梯度下降来优化这个模型,通过最小化每个真实图像与渲染出来的视图之间的误差。在多个视图上最小化这种误差能够让网络对该场景得到一个连贯的模型,如图 2 所示。

作者发现,使用很基础的优化方式来优化复杂场景的神经辐射场的话有两个问题:
- 无法收敛得到较高分辨率的表达特征
- 每个 ray 都需要采样多个点,效率不高
作者怎么解决上面两个问题的呢:
- 通过位置编码,将 5D coordinate 输入进行转换,让 MLP 能表示更高频的函数
- 提出了一个分层级采样的方法,来降低对高频场景采样的查询次数,先粗采样,再细采样。在第一步粗略采样阶段,模型沿着每条视线均匀地取若干样本,并预测它们处于物体内部或外部(即其透明度)。然后在第二步精细采样阶段,模型会在那些预测为物体内部、且靠近物体表面区域内进行更密集地采样。这大大减少了需要处理数据量,并且能够更准确地表示复杂场景。
NeRF 的特点:
- 第一点:继承了体积表征(volumetric representations)的优势,能够表征复杂真实世界中的几何形状和外观
- 第二点:能够使用基于梯度的方式来优化,克服了对高分辨率复杂场景建模时,离散体素网格带来的大量存储消耗。
什么是体积表征(Volumetric Representations):
- 一种在计算机视觉和图形学中常用的术语,指的是一种三维数据表示方法。它不仅记录了物体的表面信息,而且还记录了物体内部的信息。这种表示法通常会将一个三维对象分解为许多小的立方体或者其他形状(称为体素,voxels),每个体素包含有关该空间区域内部内容(如颜色、密度、温度等)的信息。
- Volumetric Representations 可以捕获复杂真实世界中几何形状和外观的详细信息,并适用于各种 3D 建模和视觉任务。
- 体素(Voxel)是三维空间中的最小数据单元,类似于二维图像中的像素。在处理高分辨率的三维数据时,需要大量的体素来精确地表示物体或场景。这就意味着你需要更多的存储空间和计算资源来处理和存储这些信息。例如,假设你有一个1000x1000x1000 的体素网格,在这个网格中每个体素都需要一定量的内存来保存颜色、密度等信息。那么总共就有10亿个体素需要被处理和存储,这将消耗大量内存。
二、方法
2.1 神经辐射场场景表达
神经辐射场的输入:
- 3D 空间位置: x = ( x , y , z ) \text{x}=(x,y,z) x=(x,y,z)
- 2D 视觉方向: ( θ , ϕ ) (\theta, \phi) (θ,ϕ),实际使用时,将方向描述为 3D Cartesian unit vector(笛卡尔单位向量) d \text{d} d
笛卡尔单位向量:
- 一个在三维笛卡尔坐标系统中的向量,它的长度(或者说大小)为1。这种单位向量常常被用于描述空间中的方向。
- 在三维空间中,我们通常使用 i, j, k 来表示三个正交(垂直)的单位向量。其中 i 指向 x 轴方向,j 指向 y 轴方向,k 指向 z 轴方向。
- 例如,(1,0,0) 是 x 轴上的单位矢量,表示为 i;(0,1,0) 是 y 轴上的单位矢量,表示为 j;(0,0,1) 是 z 轴上的单位矢量,表示为 k。
- 任何一个 3D 笛卡尔坐标系下的矢量都可以通过这三个基本单元 vectors(i,j,k) 进行组合和表达。
神经辐射场的输出:
- 颜色: c = ( r , g , b ) c=(r,g,b) c=(r,g,b)
- 透明度/密度: σ \sigma σ
所以神经辐射场就是一个 MLP 网络 F Θ F_{\Theta} FΘ,需要优化该网络的参数来学习正确的输入输出映射关系:

作者为了实现多视角连续性:
- 限制透明度/密度 σ \sigma σ 仅和位置 x \text{x} x 有关
- 限制输出 RGB 颜色 c \text{c} c 同时和位置 x \text{x} x 及视觉方向 d \text{d} d 有关
所以 MLP 的流程如下:
- 首先,使用 8 层全连接层(使用 ReLU 激活,每层 channel=256)处理输入的 3D 位置坐标 x \text{x} x,输出透明度 σ \sigma σ 和 256-d 特征向量
- 然后,将上面的 256-d 特征向量和视觉方向 d \text{d} d 进行 concat,送入单层全连接网络(使用 ReLU 激活,每层 channel=128),输出和视觉有关的 RGB color
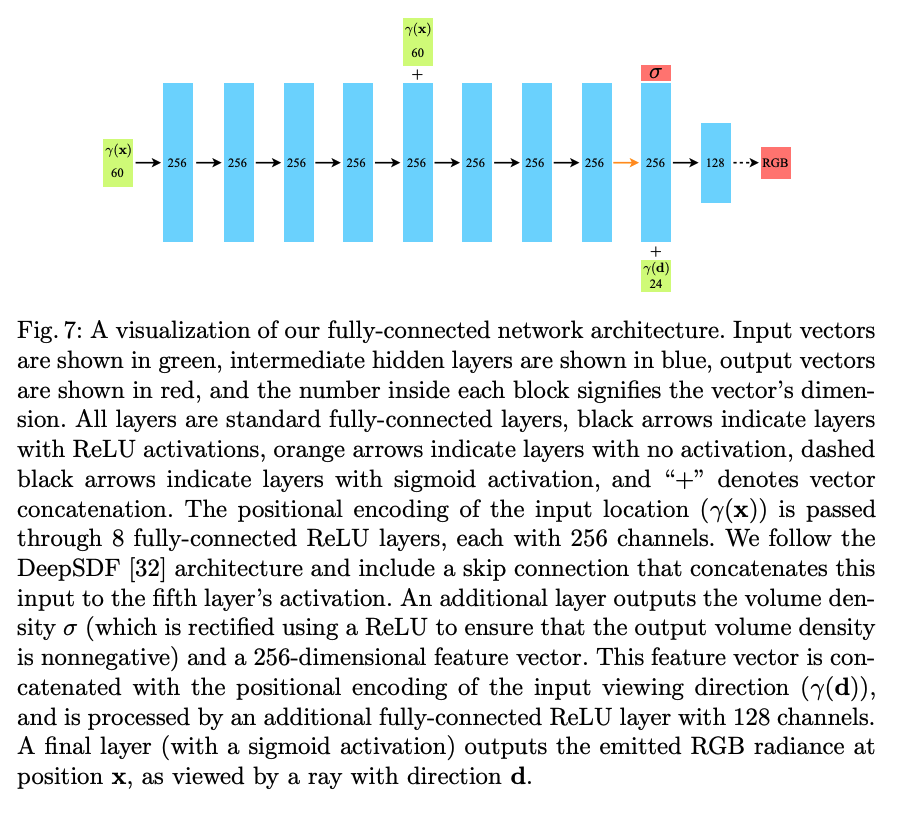
如图 3 展示了本文方法如何使用观察角度来表达 non-Lambertian effects
-
“非朗伯效应”(non-Lambertian effects)是指物体表面的反射特性不遵循朗伯定律(Lambert’s Law)。
-
朗伯定律是光学中的一个基本原理,它描述了当光线照射在理想的散射表面或者完全漫反射表面上时,出射光强度只与入射光强度和入射角有关,与观察角无关。然而,在现实生活中,许多物体并不符合这一规律。例如,镜子、金属等具有镜面反射特性的物体就会产生非朗伯效应。

如图 4 展示了当训练模型时不使用视觉方向,只使用空间位置的情况下,很难表示镜面反射(specularities)的效果:
- 镜面反射是指光线照在平滑物体表面(如镜子或光滑金属)时,按照入射角等于反射角的规律进行反射的现象。这种现象通常会使物体表面产生亮点或高光区域。如果一个模型不能很好地处理这种效果,那么它就可能无法准确地再现真实世界中具有镜面特性的物体所展示出来的视觉效果。

3.2 使用辐射场来进行立体重建
本文中,使用 5D 神经辐射场来表达一个位置的透明度和颜色
作者使用经典的立体渲染[16] 方法来渲染一个光线 ray 穿过场景得到的颜色
透明度/立体密度 σ ( x ) \sigma(\text{x}) σ(x) 可以解释为在位置 x 处 ray 终止的微分概率。
当相机光线 ray r ( t ) = o + t d r(t) = o + td r(t)=o+td 的最近距离为 t n t_n tn, 最远距离为 t f t_f tf 时,预期颜色 C ( r ) C(r) C(r) 是:
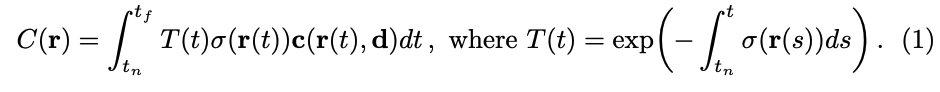
- 函数 T ( t ) T(t) T(t) 表示沿着光线 ray 从 t n t_n tn 到 t t t 的累积透射率,也就是光线从 t n t_n tn 到 t t t 不碰撞其他粒子的概率
- 使用本文中的连续神经辐射场渲染图像需要对 camera ray 估计这个积分 C ( r ) C(r) C(r)
确定性积分法通常用于渲染离散化的体素网格,会限制表示的分辨率,因为在固定的离散位置集合中只会查询 MLP(多层感知器)。
作者在数学角度使用数值积分法来估计这个连续积分,使用了一种分层抽样方法,在这种方法中,我们将 [ t n , t f ] [t_n, t_f] [tn,tf] 划分为 N 个等间隔的区间,并在每个区间内随机均匀地抽取一个样本,也就是在沿着这个 ray 经过的路线上均匀的采样,作为采样点来参与计算:
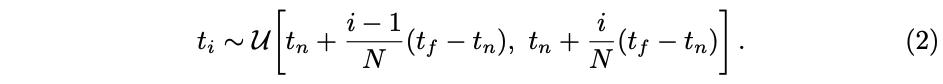
虽然这里使用的离散样本集合来估计积分,但这种分间隔的抽样能够表示连续的场景,所以能够使用这些采样点来估计 C ( r ) C(r) C(r) [26],这里的 (1-exp) 也称为 α \alpha α:
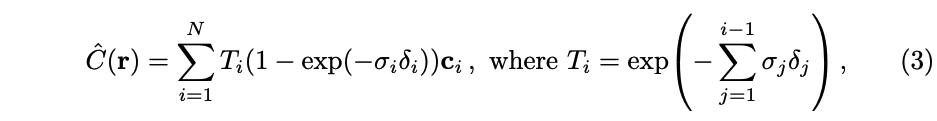
- 其中, δ i = t i + 1 − t i \delta_i=t_{i+1}-t_{i} δi=ti+1−ti 表示间隔采样的距离
3.3 优化神经辐射场
作者引入了两点优化来实现对高分辨率场景的优化:
- 1)引入了位置编码来帮助 MLP 表达高频函数
- 2)引入了分层采样来更高效的对高频表达来采样
3.3.1 位置编码
之前的工作证明了,神经网络更偏向于学习低频的函数表达,所以对高频变化(如高频的颜色和几何形状的变化)的表现就不太好
之前的工作还证明了,使用高频函数将输入提前编码到更高维的空间,然后再送入神经网络学习的话,能够让网络更好的学习这些高频变化
所以,本文作者借鉴了这种思想,将神经辐射场函数 F Θ F_{\Theta} FΘ 分解为两个函数: F Θ = F Θ ′ ∘ γ F_{\Theta} = F'_{\Theta} \circ \gamma FΘ=FΘ′∘γ ,更有利于提升效果:
-
γ \gamma γ:是一个映射,表示从 R R R 空间映射到 R 2 L R^{2L} R2L 空间,会在 x \text{x} x 的三个坐标上使用(L=10),也会在笛卡尔空间方向向量 d d d 使用(L=4)
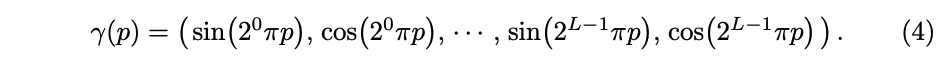
-
F Θ ′ F'_{\Theta} FΘ′:仍然是 MLP 结构
此外,作者还使用了 Transformer 中常用的位置编码,Transformer 使用位置编码来为离散序列标记顺序
而本文中使用的位置编码,是为了将 3D 连续输入坐标映射到更高维度的空间中,以便让 MLP 更容易地近似高频函数
为什么不能直接使用 3D 坐标来学习:
- 直接使用原始的、连续的3D坐标作为输入可能会导致一些问题。
- 学习难度:神经网络通常更擅长处理分布有规律、归一化后的数据。对于原始的3D坐标,其数值范围可能相当大,并且没有明显规律,这使得模型难以从中学习到有效特征。
- 表达能力:如果我们希望模型能够生成复杂且高质量的3D渲染图像,那么模型需要能够捕捉到空间中非常精细和复杂的信息(如几何形状、纹理等)。然而,如果只用原始坐标作为输入,那么模型可能无法获取足够多这样的信息。
为什么要使用位置编码:
- 位置编码能够帮助模型更好地理解和表示3D空间。
- 在深度学习中,神经网络通常很难直接处理连续的数值输入,比如3D空间中的坐标。如果我们直接将坐标值输入到神经网络,那么网络将很难从这些数值中提取出有用的特征和模式。
- 因此,在NeRF中引入了位置编码这个概念。位置编码是一种对原始坐标进行预处理的方式,它可以将连续的数值转化为一种形式,使得神经网络能够更好地识别和处理。具体来说,在NeRF中使用了一种基于正弦和余弦函数的位置编码方法。这样可以将原始坐标映射到一个更规范化、且有规律性的高维空间,在这个空间中,神经网络更容易学习和提取特征。
- 通过使用位置编码,可以大大增加模型输入数据的维度,并且使得每个不同坐标都对应一个唯一且独特的高维向量。这样就为模型提供了更多、更精细级别上的信息,使其能够捕捉到3D场景中复杂、高频率(如几何边界或纹理)等信息。我们可以让模型更好地捕捉到复杂、高频率(如几何边界或纹理)等信息,并且能够生成出质量更高、细节更丰富的3D渲染图像。
3.3.2 分层立体采样
在传统的NeRF渲染中,每一条光线都会在多个位置进行采样,并对神经辐射场模型进行评估。但这种方法效率低下,因为它会重复采样那些对最终图像没有贡献或被遮挡的区域。
所以 NeRF 中提出了层级采样,也是 NeRF(神经辐射场)中用于提高渲染效率的关键技术。
-
首先,使用粗糙网络进行分层采样。这个过程会在每条光线上选择Nc个位置进行评估。
-
然后,根据粗糙网络的输出结果,在每条光线上选择更多具有潜在重要性的位置。这些位置是通过计算权重值来确定的,权重值反映了每个可能新采样点对最终图像可能产生影响的大小。在这些新选出来的位置(通常数量为Nf)上,再次评估神经辐射场模型。但这次使用更详细、更复杂(因此也更准确)的精细网络。
-
最后,将从所有采样点收集到的信息合并起来生成最终图像。具体来说,他们会利用从粗糙网路得到 alpha 复合颜色重新构造成沿着光线所有采样颜色 ci 的加权总和。通过这种方式,NeRF可以更有效地利用计算资源,在关键区域进行更密集的采样以获得更好的渲染结果。
在第一步粗略采样阶段,模型沿着每条视线均匀地取若干样本,并预测它们处于物体内部或外部(即其透明度)。然后在第二步精细采样阶段,模型会在那些预测为物体内部、且靠近物体表面区域内进行更密集地采样。这大大减少了需要处理数据量,并且能够更准确地表示复杂场景。
3.3.3 具体实现细节
作者优化网络时使用了一个场景的多个角度采集到的图片,对这些真实图片,需要使用 COLMAP 这个开源的结构光软件包,来估计当时拍照时的相机姿态、内参、场景边界等。
合成图像时,给定真实的参数,包括需要的相机姿态、内参、场景边界,来生成该场景的图片
在每个 iter 中,随机采样 camera ray 作为一个 batch,然后使用层级采样来从 coarse 网络中查询 N c N_c Nc,从精细网络中查询 N c + N f N_c+N_f Nc+Nf
然后使用立体渲染来从这些采样点钟渲染出每个 ray 的颜色,loss 是渲染出的颜色和真实颜色的 MSE,需要同时计算 coarse 和 fine network:

- batch:4096 rays
- 采样点: N c N_c Nc=64, N f N_f Nf=128
- 优化器:Adam
- 学习率:开始为 0.0005,逐步降低为 0.00005
- 每个场景优化大约需要 100-300k iters,单个 V100 需要 1-2 天
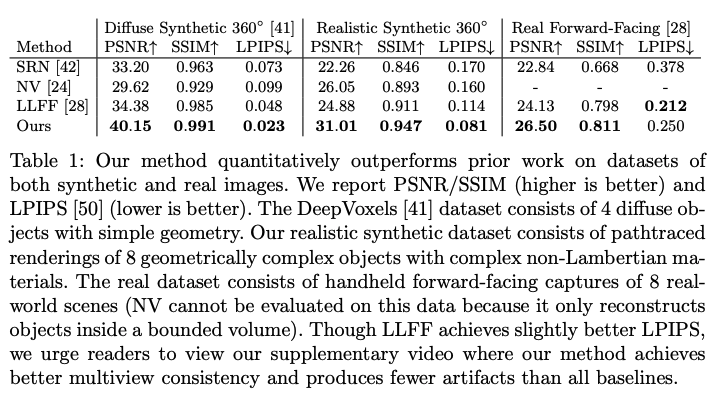
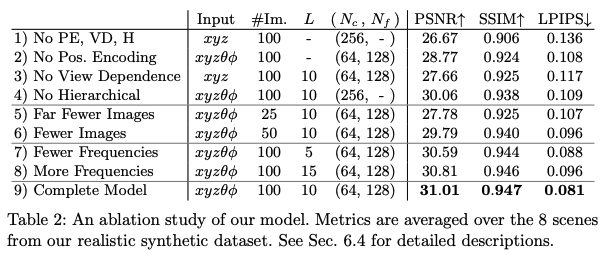
三、效果