1539. 第 k 个缺失的正整数
-
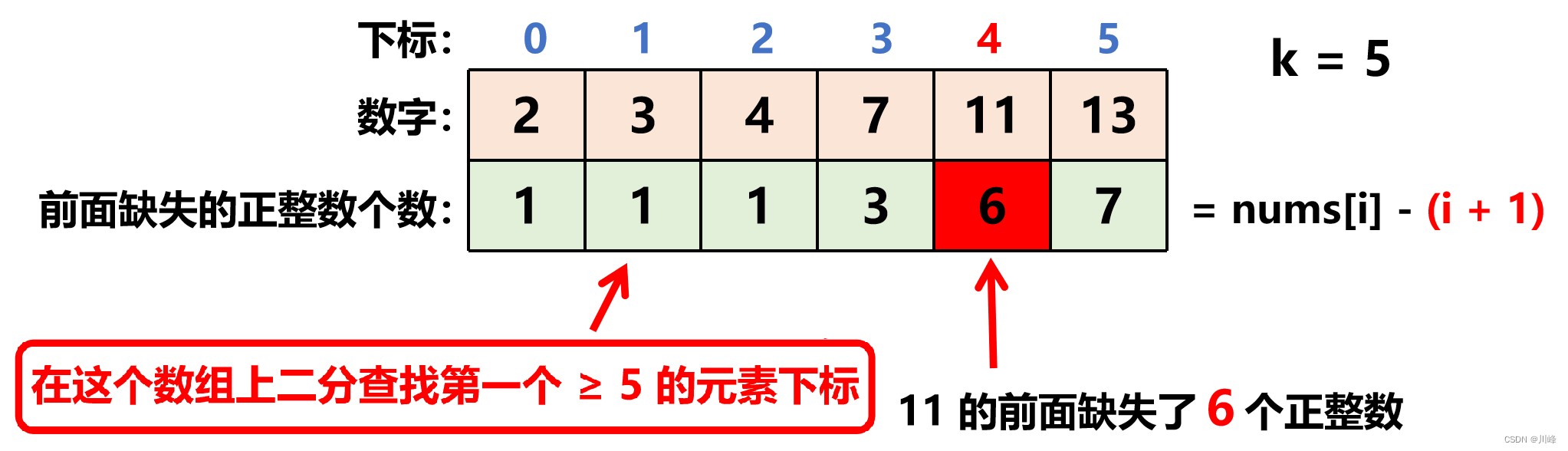
1. 二分 ,一个严格升序 正整数 数组在没有数字缺失的情况下满足: nums[i] = i + 1 ,如果有缺失,则每个 下标 i 上的数字前面缺失的正整数个数为: nums[i] - (i + 1) (没有缺失的情况 num[i] - (i + 1) 正好等于 0)
-
因此可以在 下标 [0, N] 上二分 ,查找目标是【 前面缺失的正整数个数 】 ≥ k 的第一个数。
-
每次二分判断的点就是【 mid前面缺失的正整数个数 】: miss = nums[mid] - (mid + 1)
-
如果 miss < k , 就往 右边二分 ,如果 miss >= k , 就往 左边二分 。
-
跳出二分循环时, L == R , R 就是要找的下标,即该位置上的数是第一个满足 前面缺失的正整数个数 ≥ k 条件的。
-
最终缺失的数字就是 R + k 。

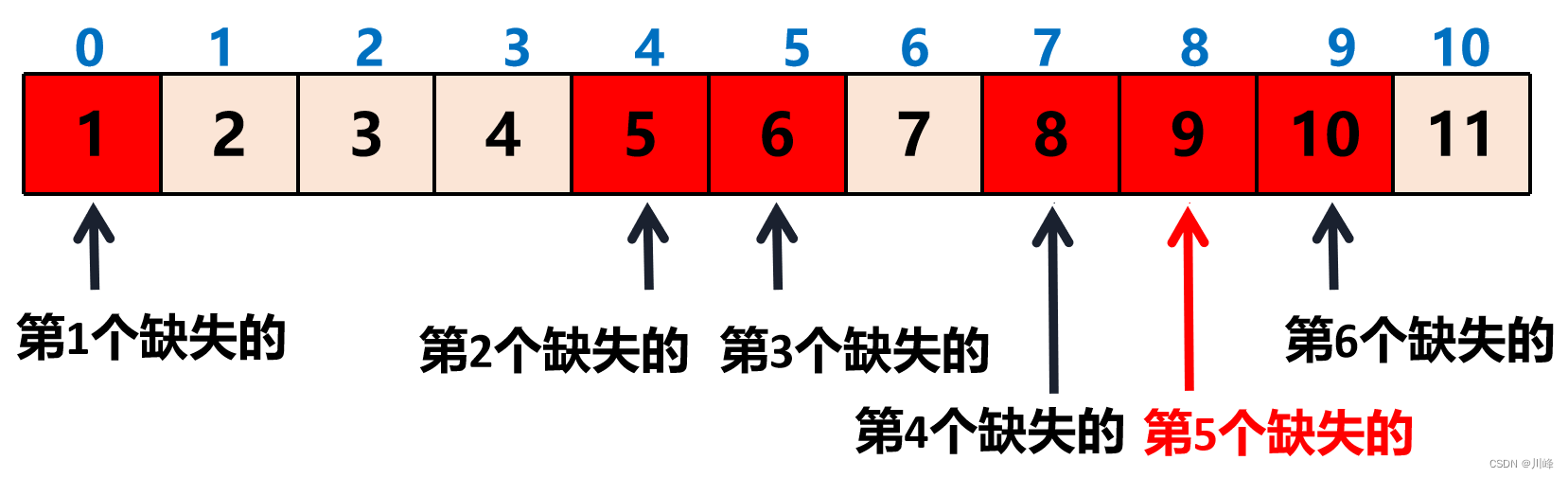
我们总结一下:
- 1)二分查找的数组不是原始数组,而是由原始数组的每个元素通过公式 nums[i] - (i + 1) 生成的新的数组上进行二分
- 2)二分查找的目标是大于等于 k 的第一个位置下标
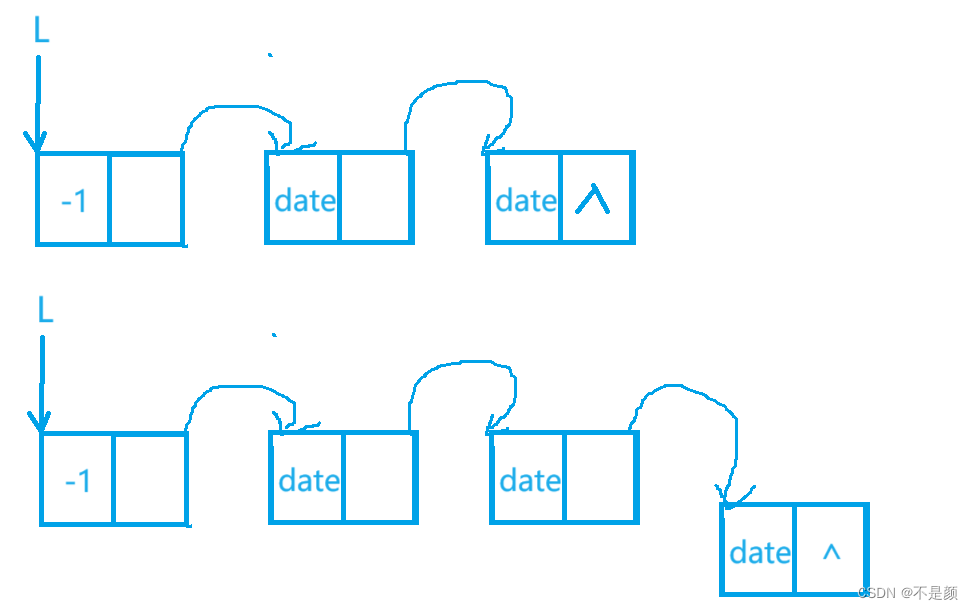
当我们找到了这样满足条件的下标之后(也就是退出 while(L < R) 循环时的 R),该如何计算缺失的第个数呢?这时我们可以将包括 R 位置的数在内和前面缺失的数字组成的数组区间进行一下重新分布,如下图:
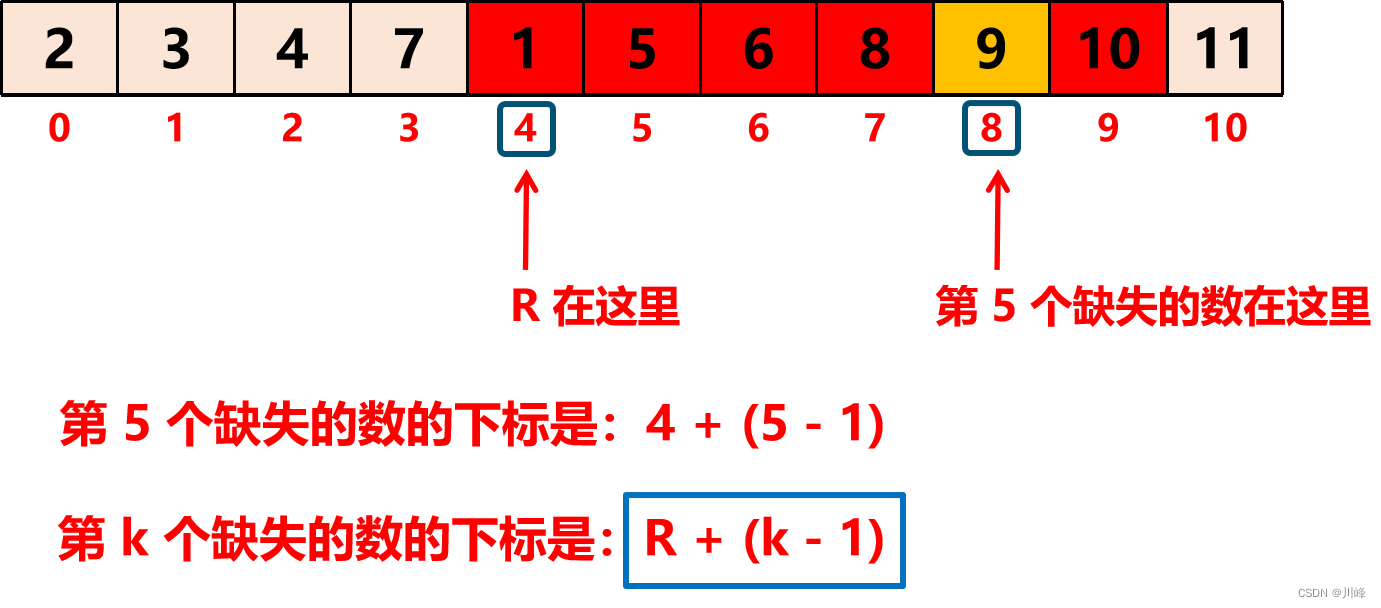
也就是说找到了 R 即找到了缺失的数字原本的下标是 R + (k - 1) ,我们回顾一下数组中没有缺失数字的情况:
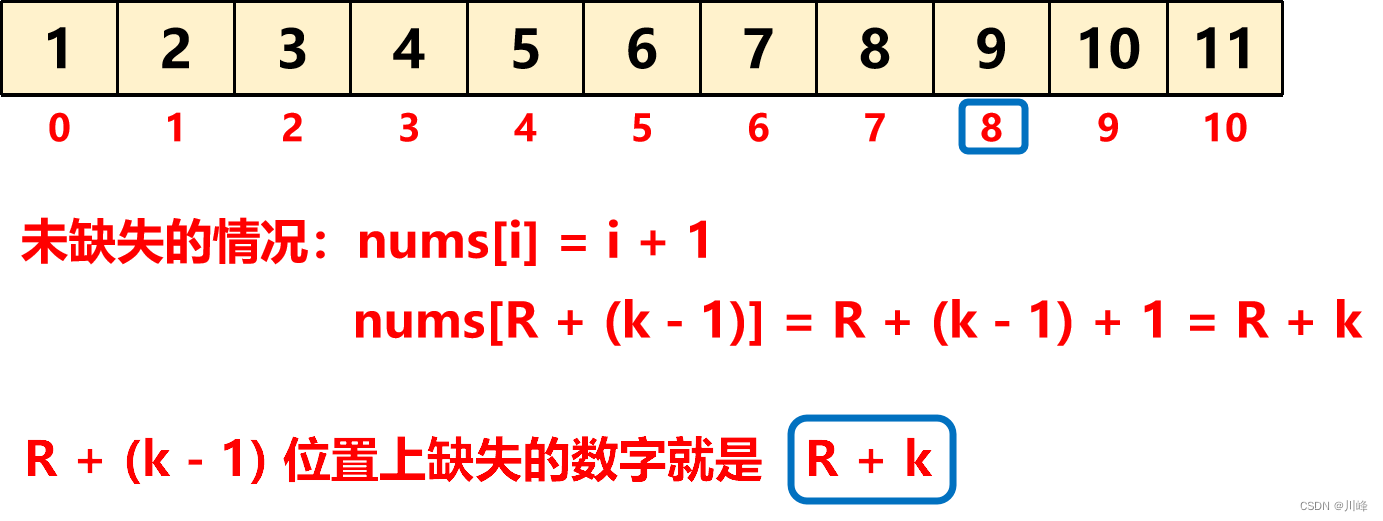
所以我们直接用 R + k 就算出了第 k 个缺失的数字。
此外,我们还有两种特判情况,可以简化处理:


注意:这里 R 要取到数组的长度 N,而不是 N - 1,这是因为有可能数组中所有数字前面缺失的个数都小于 k,也就是说第 k 个缺失数字排在数组之后。这样 L 会不断往右边缩,最终退出循环时,L == R == N,这样通过 R + k 计算不会错过答案。参考下面的例子理解:
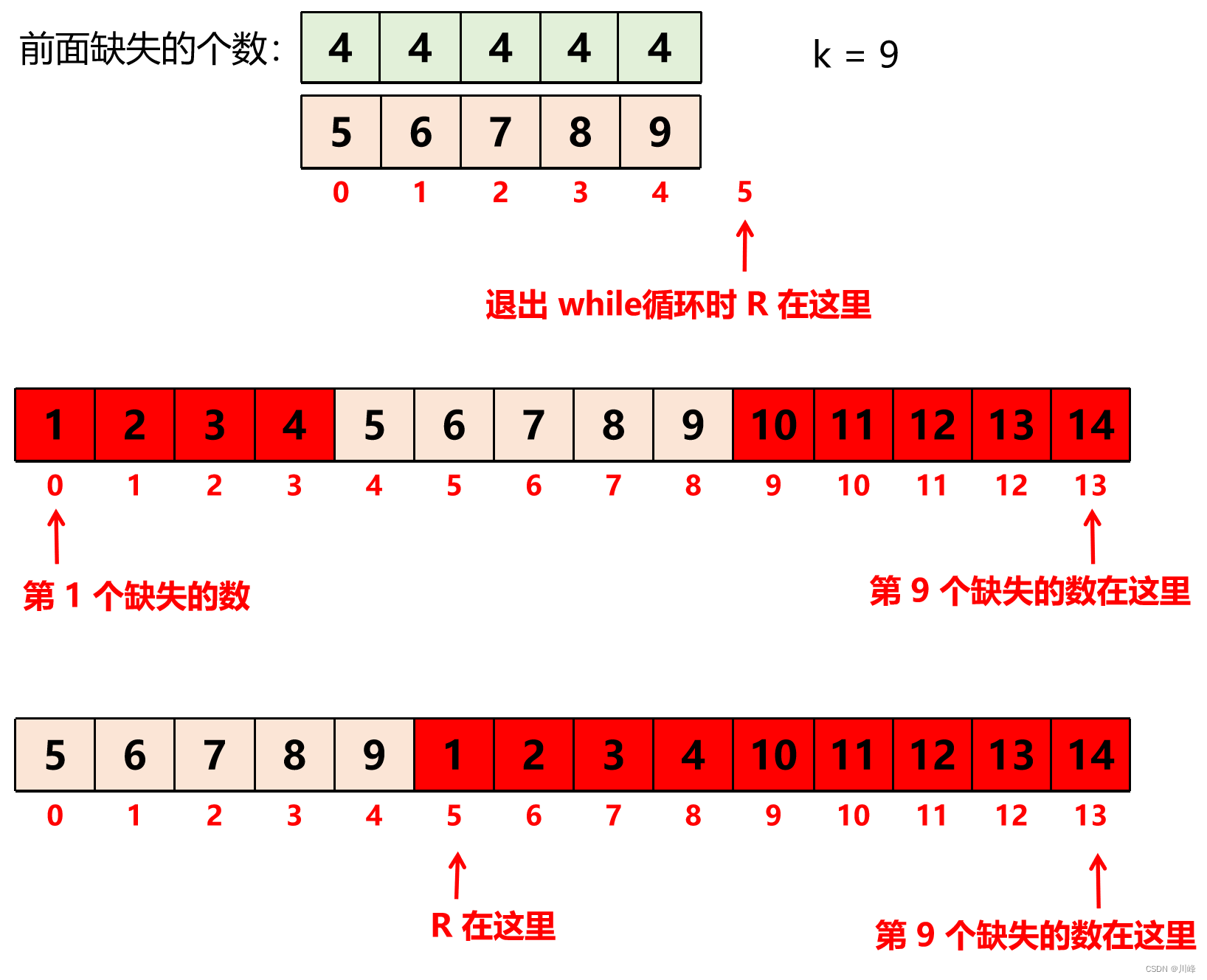
假设 R 初始取 N - 1,这里退出循环时,R = 4,R + k 得到的第 9 个数会是 13,是错误答案。
由于二分查找的过程完全覆盖了前面提到的两种特判情况,因此也可以完全省略掉特判代码,直接像下面这样写:

只不过加上特判对某些测试用例可以更快速的通过。
注意,这个题能用二分查找的前提是题目数组是升序排的,因此通过公式 nums[i] - (i + 1) 生成的对应的新数组也是升序排的。
-
2. 线性查找 ,查找判断的条件跟方法1一样,只不过由二分变成 顺序 查找 【 前面缺失的正整数个数 】 ≥ k 的第一个数 。

相对而言,这种方法的代码更加简单,但时间复杂度是 O(n),没有二分的 O(logn) 高效。这里 R 仍然要取到 N,因为数组中可能找不到 ≥ k 的第一个下标,方法1中已经分析过了。
278. 第一个错误的版本

-
二分查找 ,因为版本号是一个从1开始的升序序列,所以题目等价于二分查找第一个等于目标元素的值,即在一个升序数组中查找第一个符合错误版本的数字。


二分查找-前瞄法:
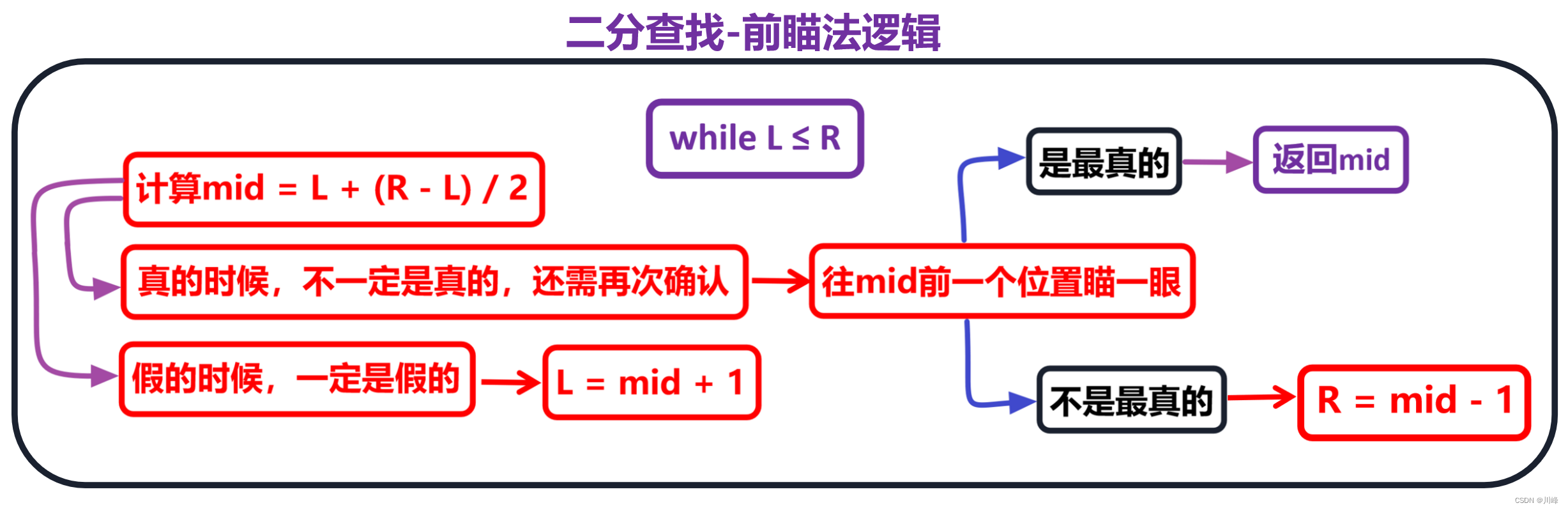

前瞄法的另一种等价的写法:

剑指 Offer 53 - II. 0~n-1中缺失的数字

-
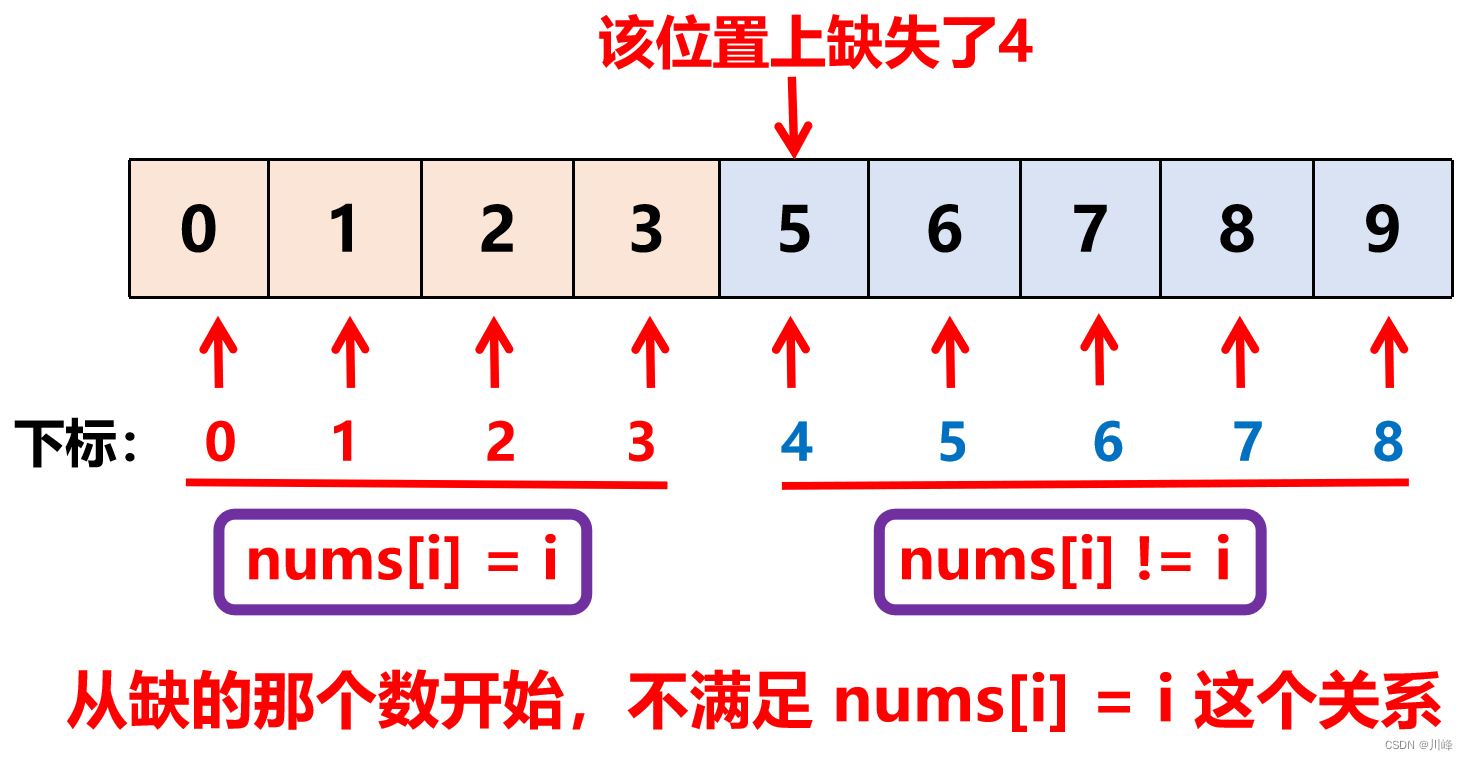
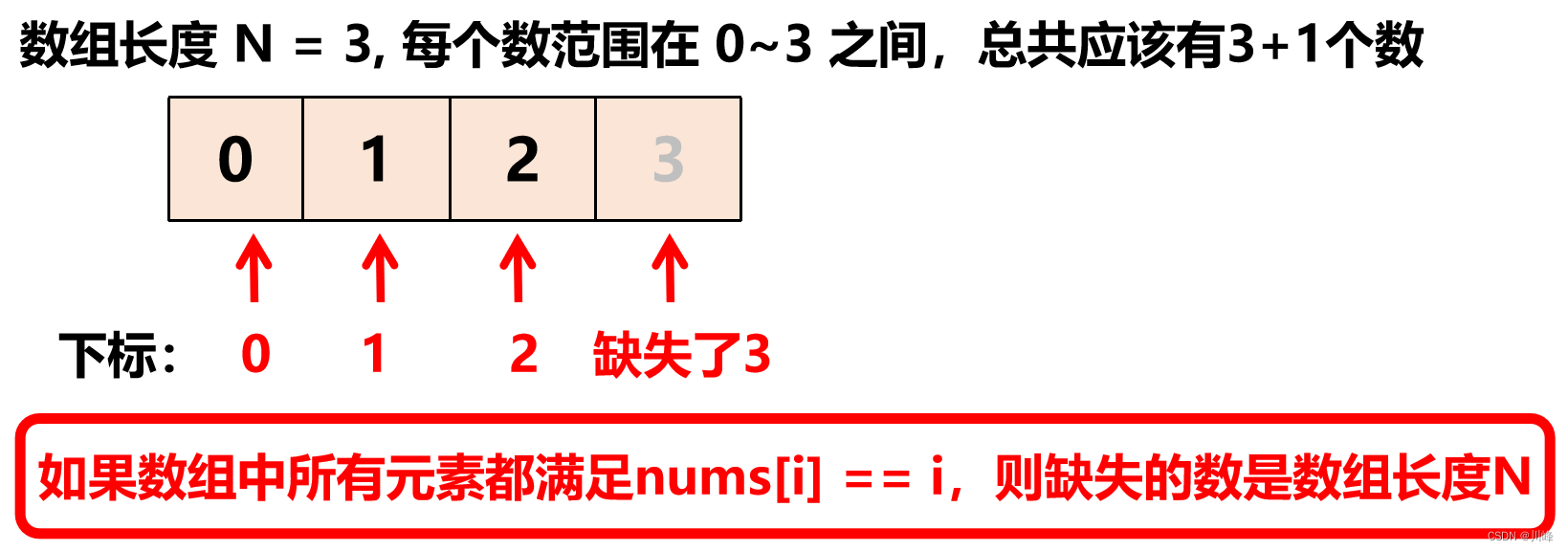
1. 二分查找 , 如果数组中 没有缺失 0~n-1 任何数,则满足 nums[i] = i , 如果缺了某个数, 从缺的那个数开始就不满足 nums[i] = i 这个关系。
-
因此数组被分成两部分: 左半部分 nums[i] = i 和 右半部分 nums[i] != i 。
-
二 分查找第一个满足 nums[i] != i 这种关系的 i 就是答案。
-
注意: 如果数组中所有元素都满足 nums[i] == i ,则缺失的数是数组长度 N 。
二分查找第一个满足某种关系的下标,有两种方法:前瞄法和区间排除法


解题思路:
-
2. 线性查找,遍历找到第一个满足 num[i] != i 的 i 就是答案。

2035. 将数组分成两个数组并最小化数组和的差

-
分治 + 二分 / 有序表 , 首先将数组分成等长的两半,对每一半的数组,通过 DFS 求出其中选 x 个数的 sum 和是多少(用 Map<Int, TreeSet> 存储因为选 x 个数的和可能有多个)
-
然后从两半数组生成的 2个Map 中寻找 N / 2 个数的组合,使其和最接近 allSum / 2 ,记作 pickSum ,而剩余的 N / 2 个数组成的数组的和就是: restSum = allSum - pickSum ,然后每次求 abs(pickSum - restSum) 并记录 最小值 就是答案。
-
Map 也可以用列表存选 x 个数的和,完了用【二分查找最后一个小于等于目标的元素】替代 TreeSet.floor 。
首先看一下如何通过 DFS 求一个数组中选 x 个数的 sum 和是多少:

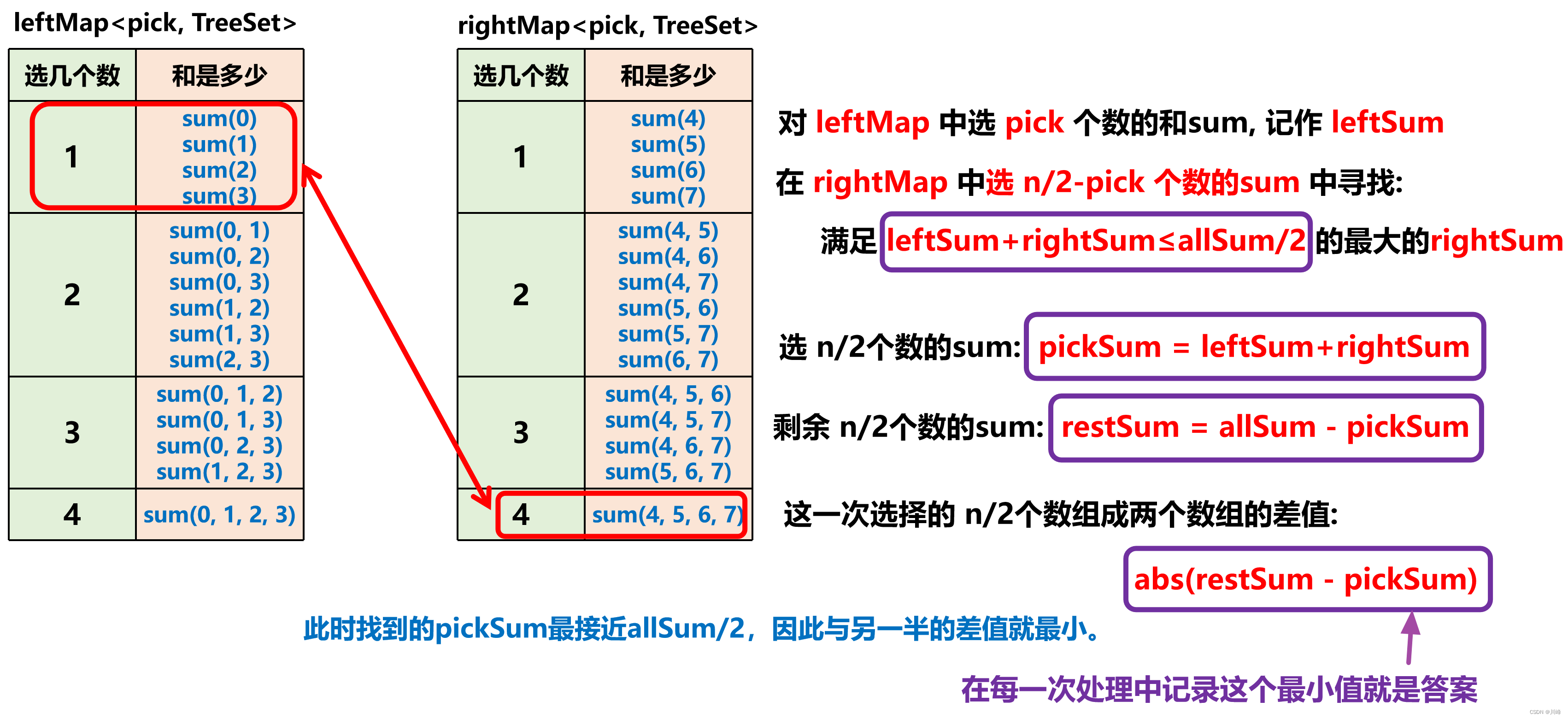

其中 TreeSet.floor() 返回 ≤ target 的最大值,也就是 ≤ target 的最后一个元素。
因此,我们也可以使用二分查找来代替 TreeSet.floor() 的功能,参考代码如下:

852. 山脉数组的峰顶索引

-
1. 线性查找 , 双指针 O(N) 参考941

-
2. 二分查找 , 区间排除法 ,
-
若 A[mid] < A[mid + 1] 说明 mid 处在 上坡 , 峰值 肯定在 [mid+1, R] 区间 ,
-
若 A[mid] > A[mid + 1] 说明 mid 处在 下坡 , 峰值 肯定在 [L, mid] 区间 。

由于题目给的是山脉数组,山峰一定存在,所以二分查找一定能找到结果,所以最后返回时可以不需要判断L==R且山峰在两端。
问题思考:常规的二分查找是在一个单调有序数组上查找,但是本题并不是一个有序数组,为什么也能用二分呢?
- 实际上题目中的数组包含一个单调递增序列(峰值左边)和一个单调递减序列(峰值右边),我们只是不知道两个序列的分割点,即峰值在哪里。
- 对于一个范围 [i, j],我们可以先找到范围 [i, j] 中间连续的两个点 mid 与 mid+1。如果 arr[mid] < arr[mid+1] ,那么可以知道峰值在范围 [mid + 1, j] 内;如 果 arr[mid] > arr[mid+1] ,那么可以知道峰值在范围 [i, mid] 内。通过这样的方法,我们可以在 O(logn) 的时间内找到峰值所处的下标。
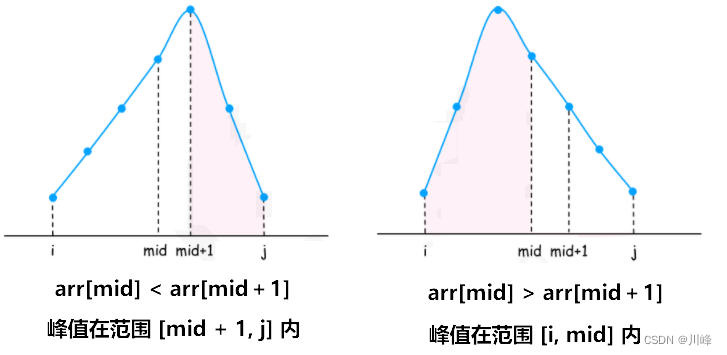
这本质上是因为峰值一定是处在单调递增序列的右边和单调递减序列的左边,也就是说对于任意一段区间而言峰值非左即右,峰值在方向上具有某种单调性,所以才能使用二分利用这种单调性来求解。
注意,941题是给一个数组判断其是否是山脉数组,这个数组不一定是山脉数组,而本题是给出一个山脉数组,找出其山峰,所以941是不能用二分查找来判断的,但是本题可以。
1095. 山脉数组中查找目标值

-
可以通过 三次二分法查找 来完成:
-
1)同852,先使用 二分法 找到山脉数组的 峰顶索引
-
2)在 上坡升序数组中二分查找目标值 ,找到就返回
-
3)第2步没找到,再到 下坡降序数组中二分查找目标值
实际上就是通过找到山峰来将数组分成了两个有序数组,在这两个有序数组中查找目标值,由于题目是要找第一个等于目标的下标值,所以需要先找上坡的,再找下坡的。
由于山脉数组是由严格单调递增/递减的序列组成,不含重复元素,所以使用标准的二分查找代码即可(不需要使用前瞄法)。


162. 寻找峰值
-
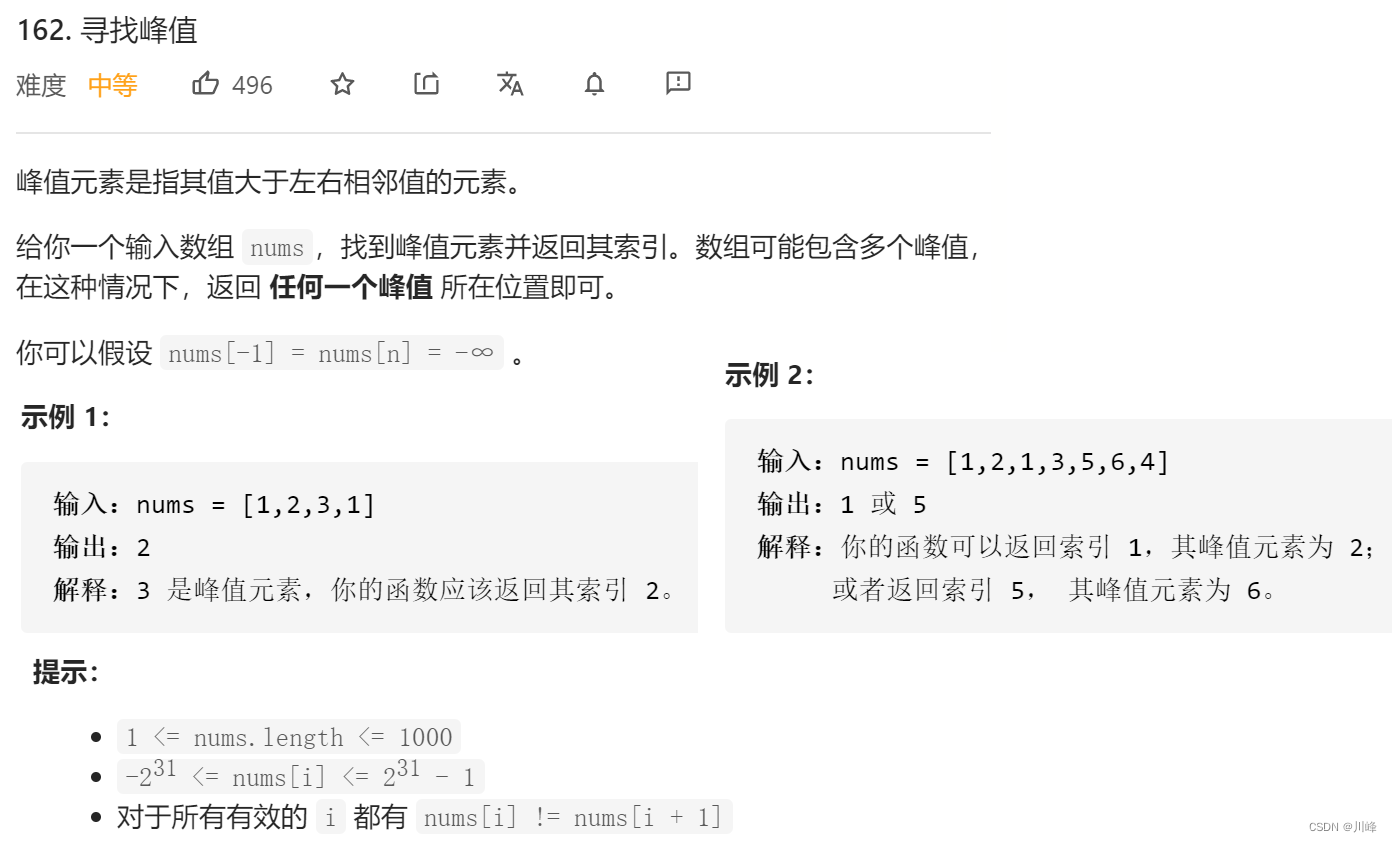
代码同852,只要找到一个山峰即可,但是本题能用 二分 有前提条件:
-
1) nums[-1] = nums[n] = -∞
-
2)由于第一条,整个数组中一定存在至少一个峰值
-
3)无重复值,数据有排他性

问题思考:为什么我们这样做二分到最后一定不会错过峰值?
当 mid 落到任意一个位置时,只可能是以下四种情况之一:
- ① 处于某个山峰,当前就是峰值
- ② 处在某个上坡,右边的值比当前大,右边绝对存在一个峰值
- ③ 处在某个下坡,左边的值比当前大,左边绝对存在一个峰值
- ④ 处在某个山谷,往左往右都能找到山峰
35. 搜索插入位置
-
二分查找第一个大于等于 target 的元素下标 ,
-
注意:如果没有找到 ≥ target 的位置,即数组元素全部 < target,则 target 应插入到数组的末尾,也就是数组长度的位置。
二分查找第一个大于等于target的元素下标有两种方法:前瞄法 和 区间排除法
前瞄法实现:

区间排除法实现:

区间排除法的另一种写法:

以上两种区间排除法的代码中,如果把 R 初始化为 N,或者把 res 初始化为 N,就可以省略掉前面的 target 比最后一个元素大的特判条件,因为这时代码包括了这一种情况。
74. 搜索二维矩阵

-
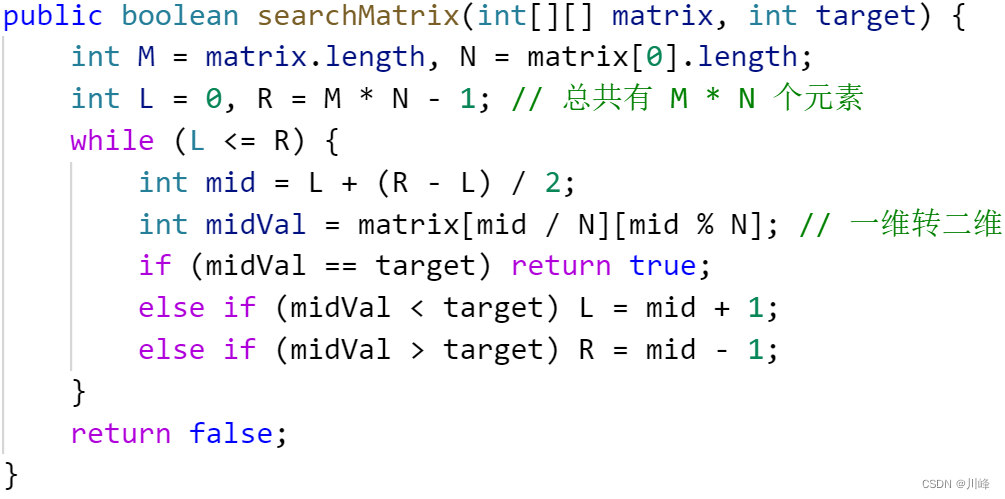
将 二维数组模拟想象成一维有序数组进行二分查找 ,二分范围 [0,M * N - 1] ,对每次二分的一维下标点 mid 转换成二维坐标值 matrix[ mid / N ][ mid % N ] 。
由于二维数组的有序特性,可以将二维数组看成一个一维有序数组,然后对其进行二分查找,但并不需要真正的将二维数组转成一维数组,只需通过坐标关系转换就可以计算得到原始位置的元素值。
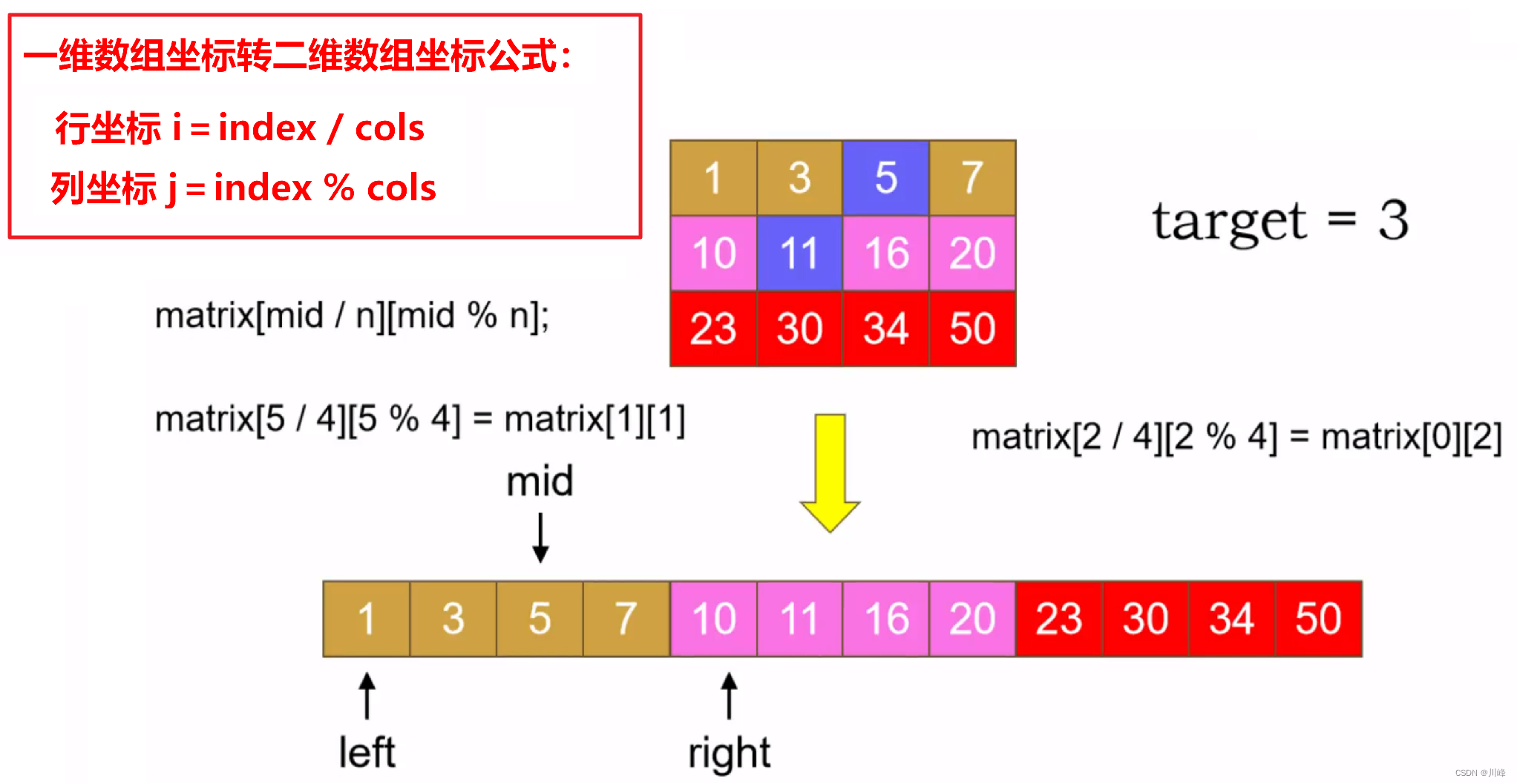
这个题主要需要记住一维坐标 index 和二维坐标 [i, j] 的转换关系:i = index / N,j = index % N,其中 N 是列数,因为按照一行一行的摆放的话,决定什么时候换行的是列数。
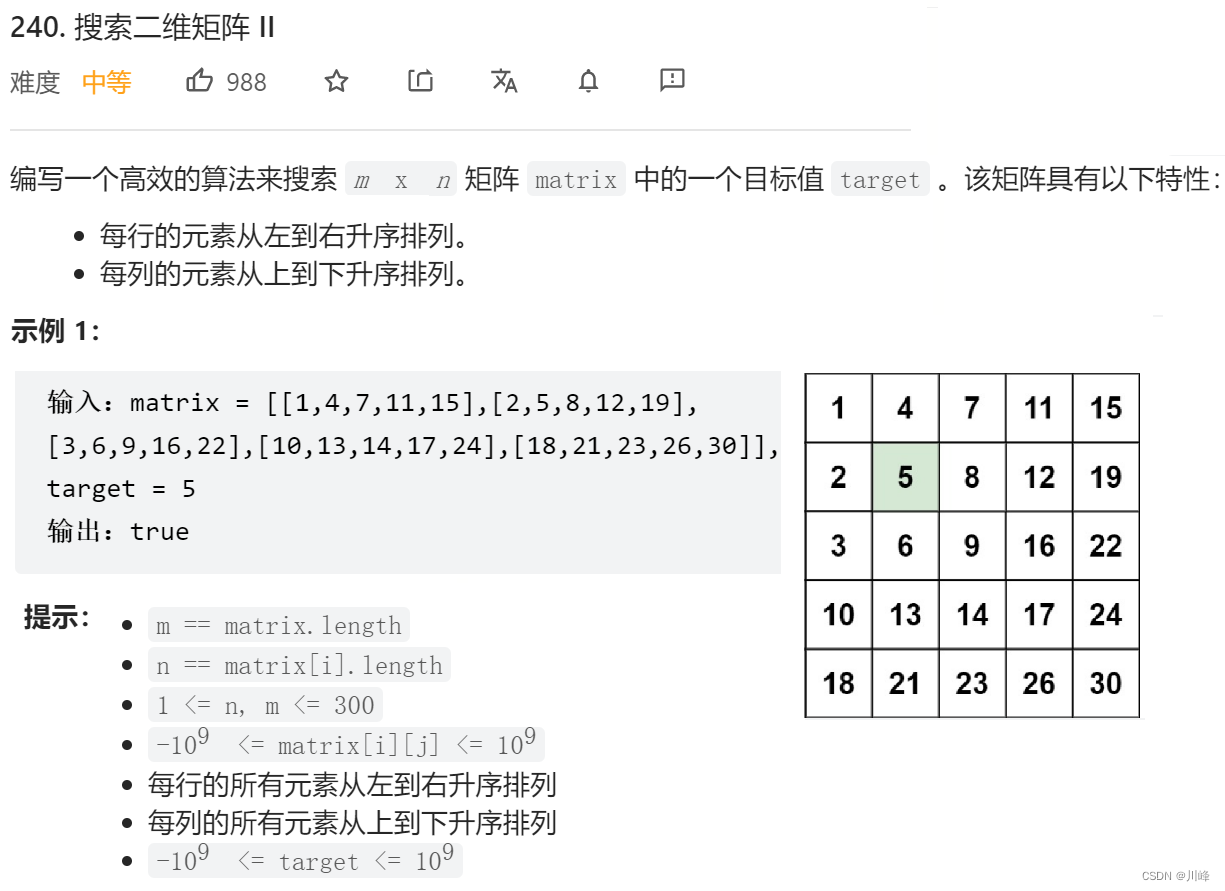
240. 搜索二维矩阵 II
-
1. 二分查找 以 对角线上的每个元素为起点 ,对 每一行 和 每一列 应用 二分查找 ,
-
对角线的长度: Math.min(M, N) ,从 i = 0 开始进行这些轮二分就可以,每次是对 第 i 行、第 i 列起点 (i, i) 二分
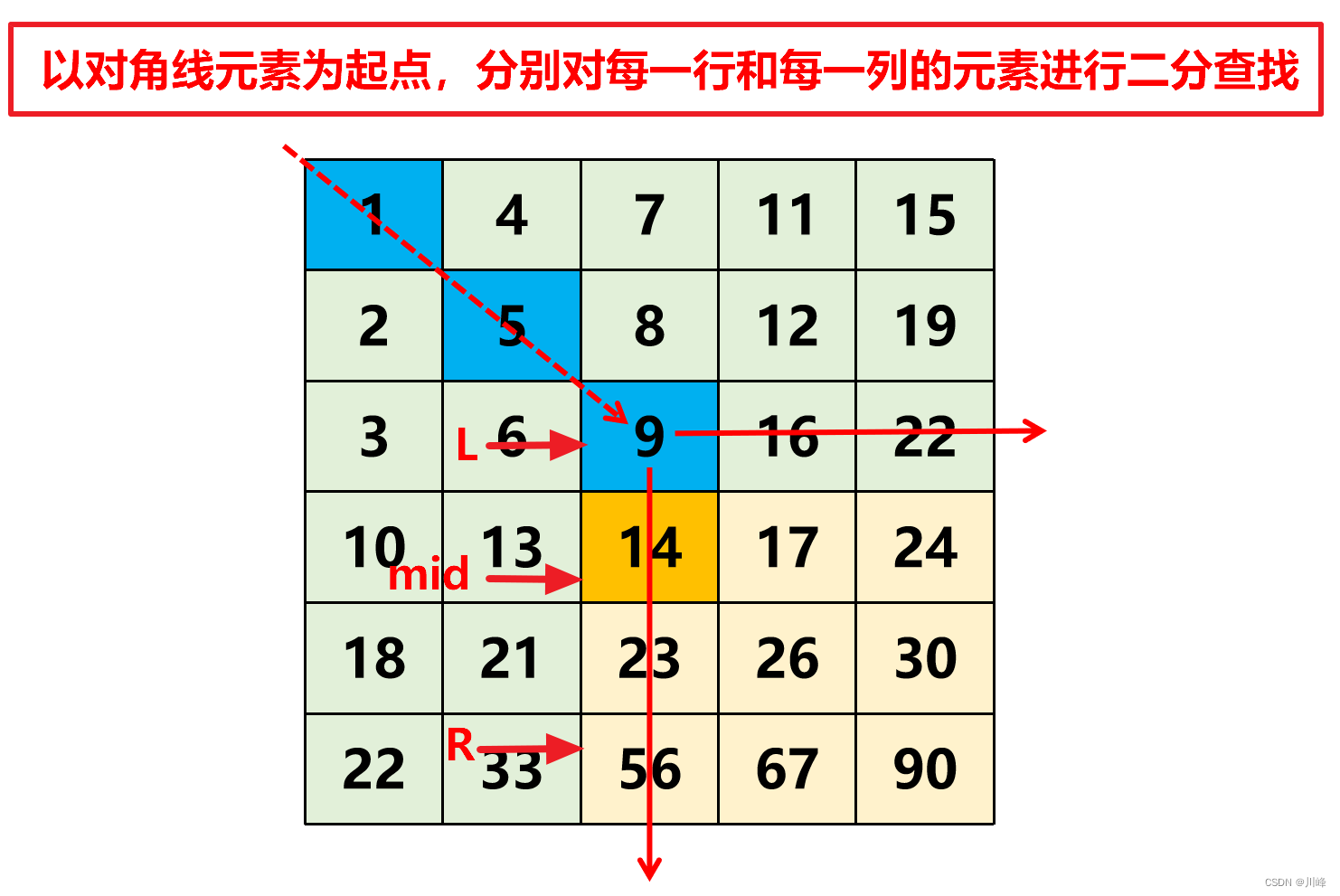


解题思路:
-
2. 线性查找,从左下角出发,遇到比目标小的往右走,遇到比目标大的往上走,遇到相等的直接返回。(或者也可以从右上角出发也具有单调性)
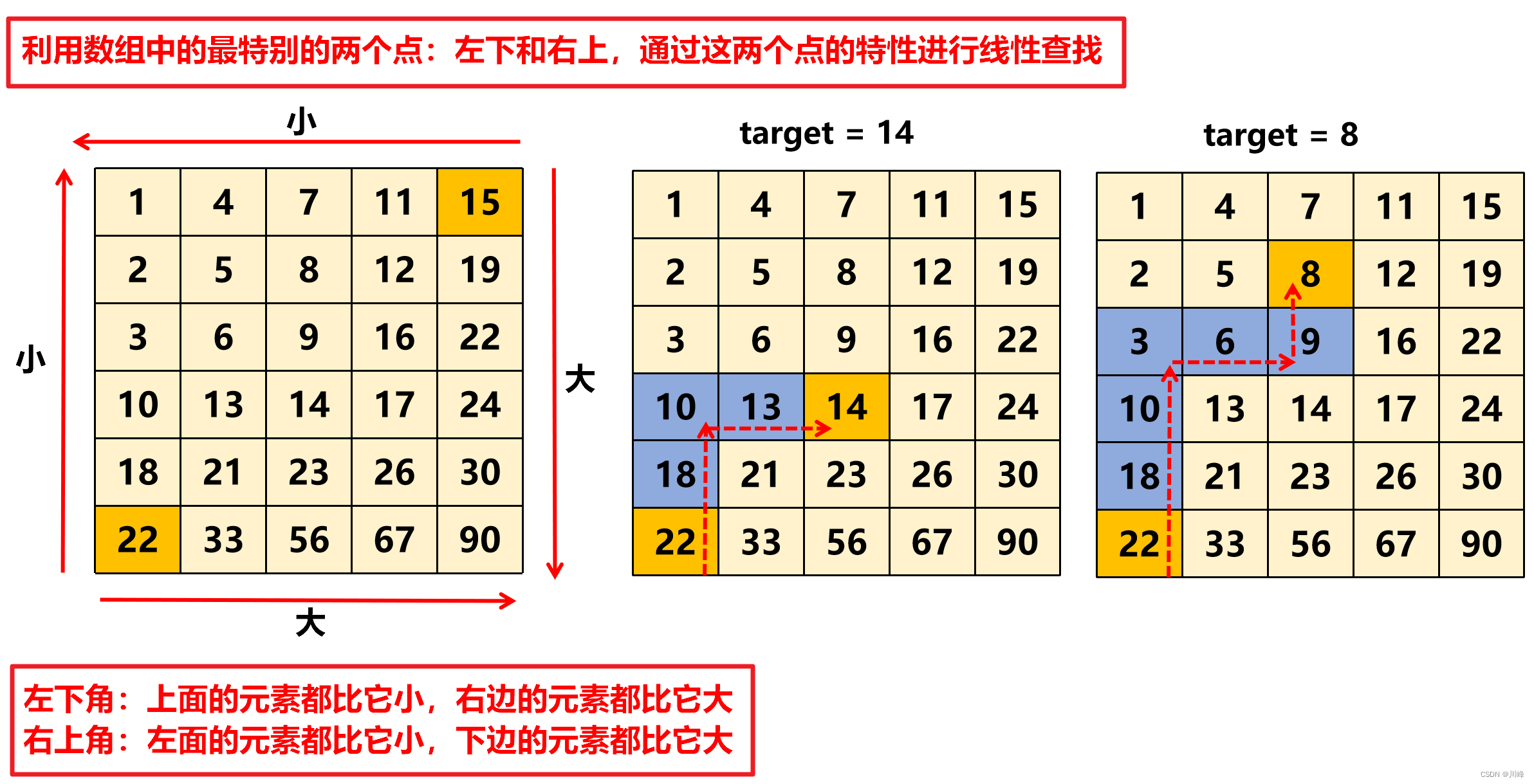
遇到比目标小的往右走,是因为右边的元素更大,目标肯定在当前元素的右边。遇到比目标大的往上走,是因为上边的元素更小,目标肯定在当前元素的上边。

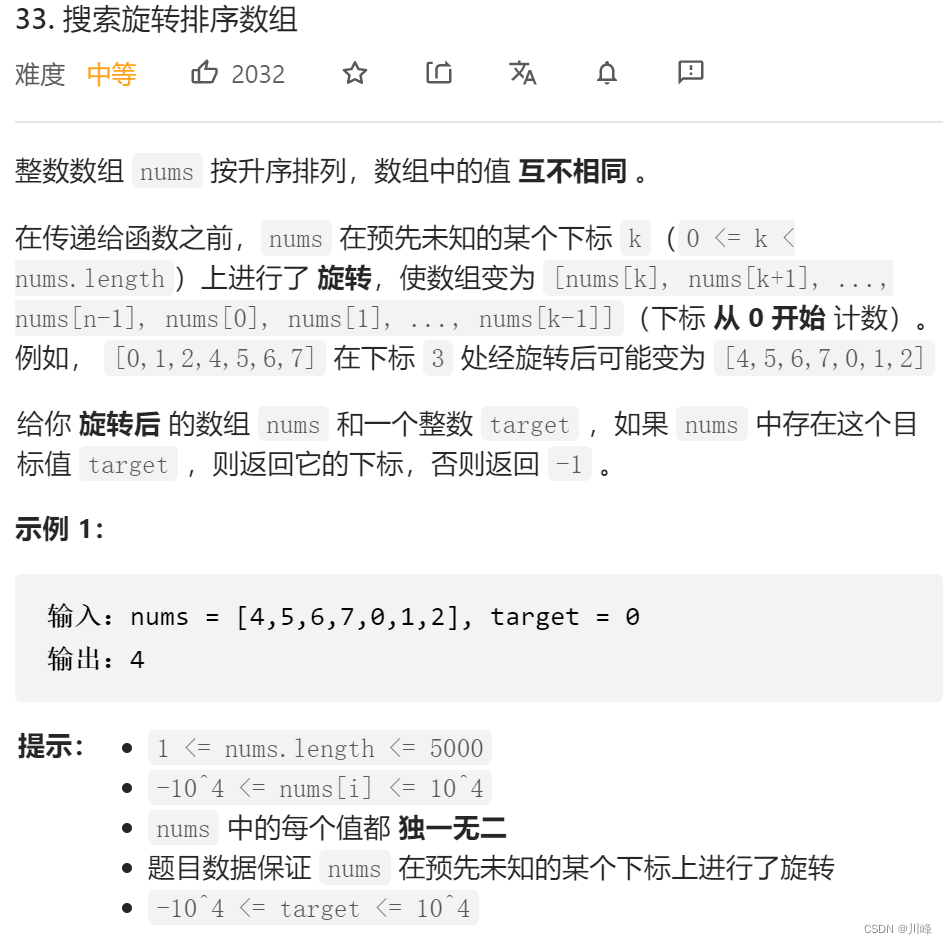
33. 搜索旋转排序数组
-
1. 二分 ,先判断 [L, mid] 和 [mid + 1, R] 哪段是 有序 的,然后判断 target 是否落在这段有序区间内,如果是就收缩对应边界至当前有序的这段区间上 ,否则就去另一边。
-
每次二分时如何判断哪一部分是有序的:若 nums[L] ≤ nums[mid] ,则 [L, mid] 是有序的,否则 [mid + 1, R] 是 有序的。
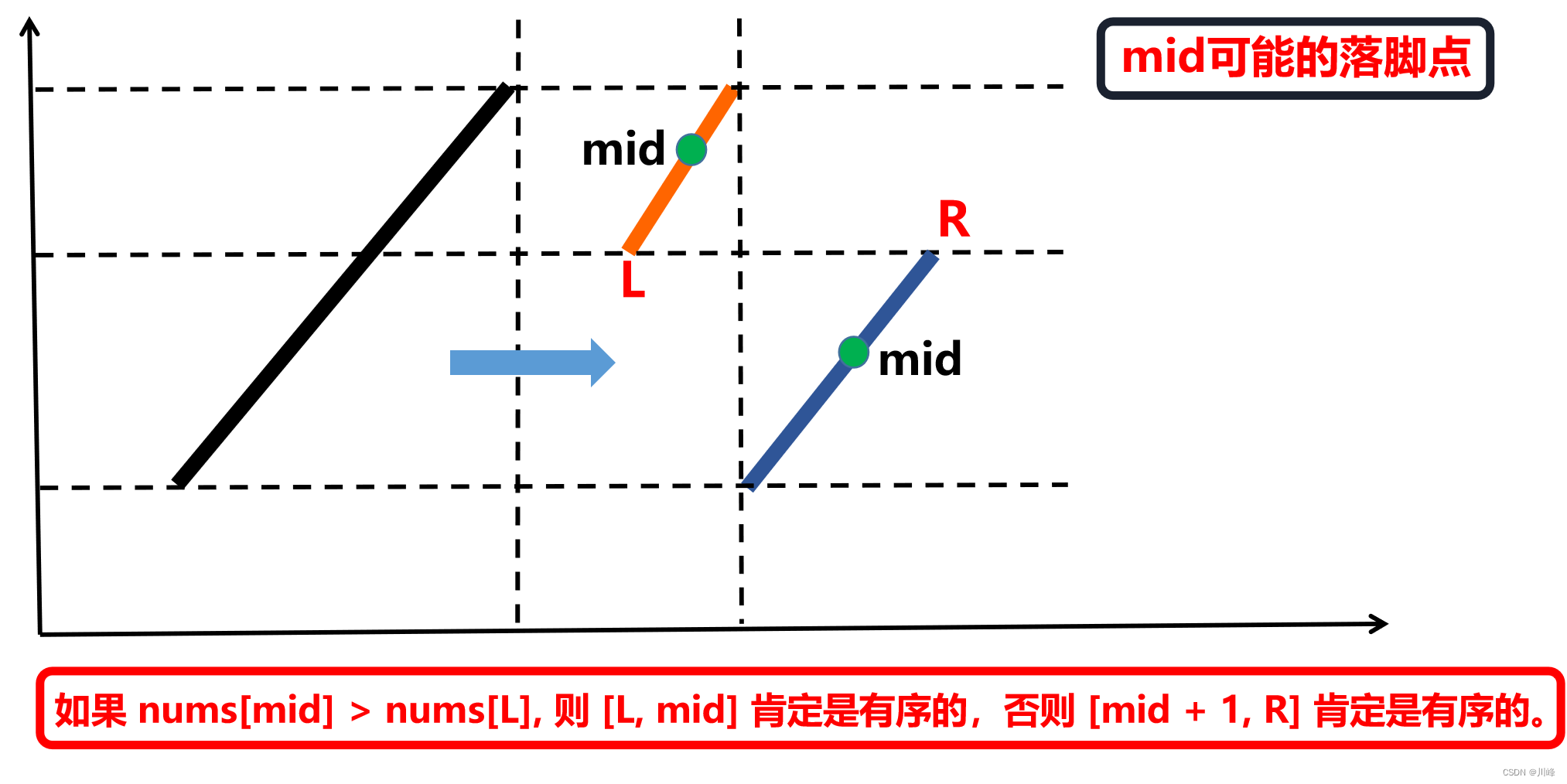
这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [L, mid] 和 [mid +1, R] 哪个部分是有序的,并根据有序的那个部分确定我们该如何改变二分查找的上下界,因为我们能够根据有序的那部分判断出 target 在不在这个部分:
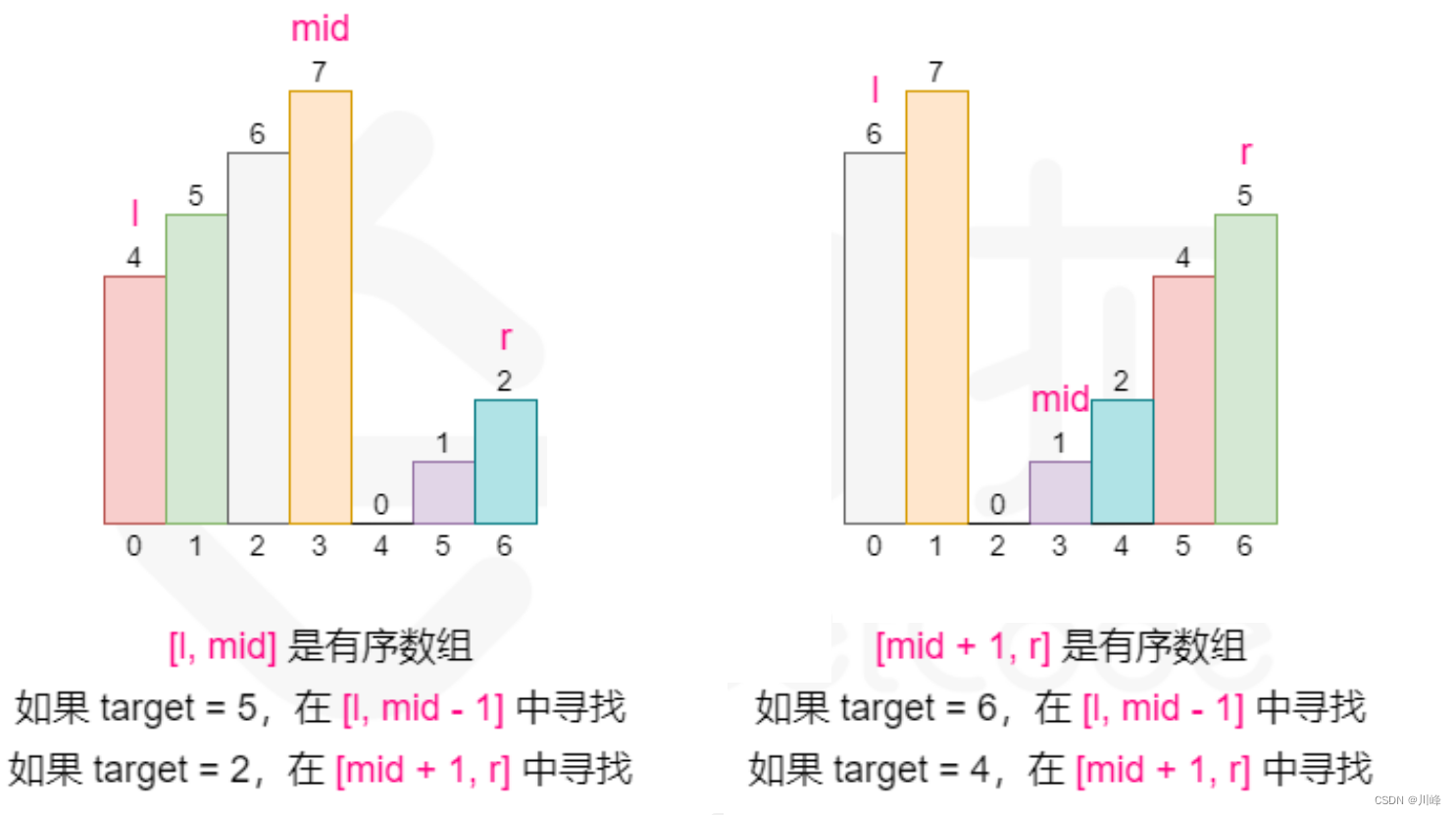
- 如果 [L, mid] 是有序数组,且 target ∈ [nums[L] , nums[mid]),则我们应该将搜索范围缩小至 [L, mid - 1],否则在 [mid +1, R] 中寻找。
- 如果 [mid + 1, R] 是有序数组,且 target ∈ (nums[mid],nums[R]],则我们应该将搜索范围缩小至 [mid +1, R],否则在 [L, mid - 1] 中寻找。

-
2. 利用极值转成有序数组 , 防御编程思想 ,若 target < nums[0] 则 target 在 右半边 ,若 target > nums[0] 则 target 在 左半边 。
-
当 target 在 右半边 时,如果 mid 在 左半边 ,将 mid 的值改成 -infinity ,当 target 在 左半边 时,如果 mid 在 右半边 ,将 mid 的值改成 +infinity 。
-
在二分查找的过程中,不断执行上面操作, 整个数组最终变成一个有序数组。
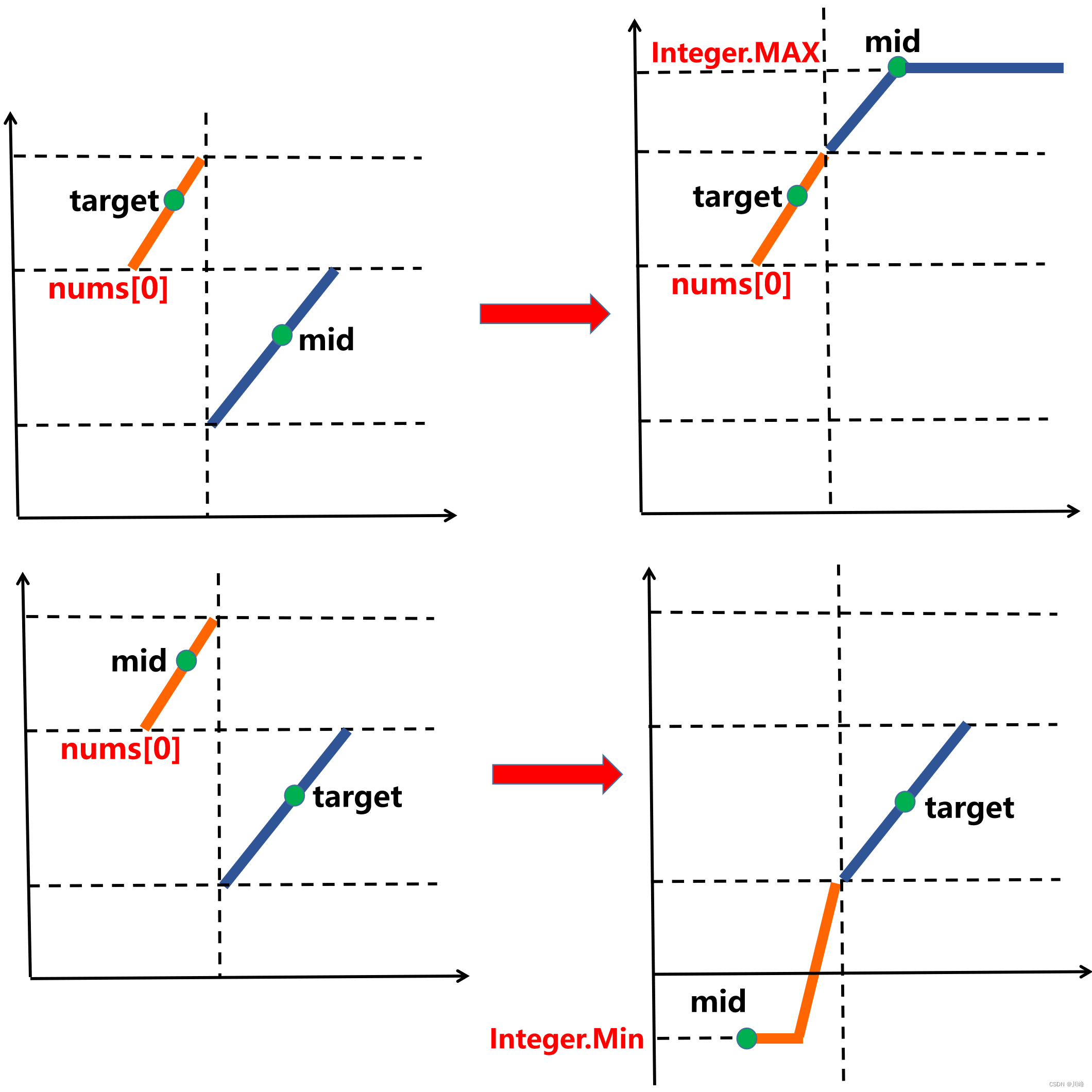
例如,对于旋转数组 nums = [4,5,6,7,0,1,2],首先根据 nums[0] 与 target 的关系判断 target 是在左段还是右段。
- 例如 target = 5,目标值在左半段,因此在 [4, 5, 6, 7, inf, inf, inf] 这个有序数组里找就行了;
- 例如 target = 1,目标值在右半段,因此在 [-inf, -inf, -inf, -inf, 0, 1, 2] 这个有序数组里找就行了。
- 如此,我们又双叒叕将「旋转数组中找目标值」 转化成了「有序数组中找目标值」

注意:这里只需要与 nums[0] 进行比较就可以定位 target 或 nums[mid] 是位于左半边还是右半边了(不能与nums[L]b比较)。
81. 搜索旋转排序数组 II

-
二分 + 去重 ,同33,只是多了 重复元素 , 当数组中有重复数时,可能会有 arr[L] = arr[mid] = arr[R] ,此时 无法判断 [L, mid] 和 [mid+1, R] 哪个是有序 的, 此时我们只需要让 L++ , R-- ,跳过相同的值,然后在新区间上继续二分查找。
例如 nums=[3,1,2,3, 3,3,3],target=2,首次二分时无法判断 [0,3] (即[3,1,2,3]) 和 [4,6](即[3,3,3]) 哪个是有序的,因为33题的二分中我们判断哪一段有序是根据 num[L] 与 nums[mid] 的大小来判断的,但此时二者都是相等的,所以无法做出判断。对于这种情况,我们只能选择 L++,R--,然后在新区间上继续二分查找。

问题思考: L++,R-- 这个操作在跳过相同的重复元素时,有没有可能会跳过答案呢?
- 在上面代码中,nums[L] == nums[mid] && nums[mid] == nums[R] 的 if 判断是写在 nums[mid] == target 的 if 判断后面的,也就是说执行到这里时,nums[mid] 肯定不等于 target,因此收缩两边相同的值,当然也不会跳过答案了。(这也提醒我们要注意这两个if判断的先后顺序,如果颠倒了肯定不行)
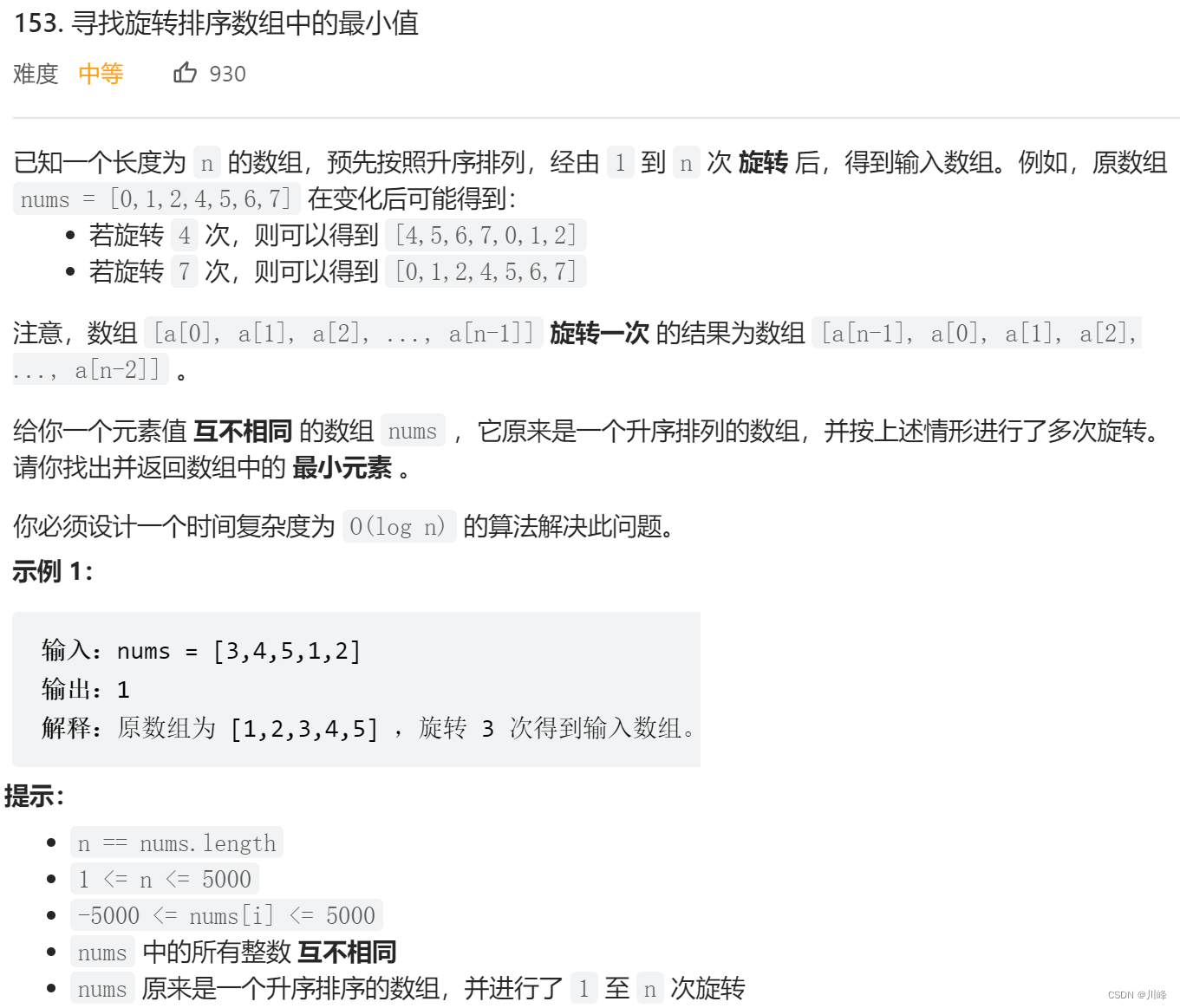
153. 寻找旋转排序数组中的最小值
-
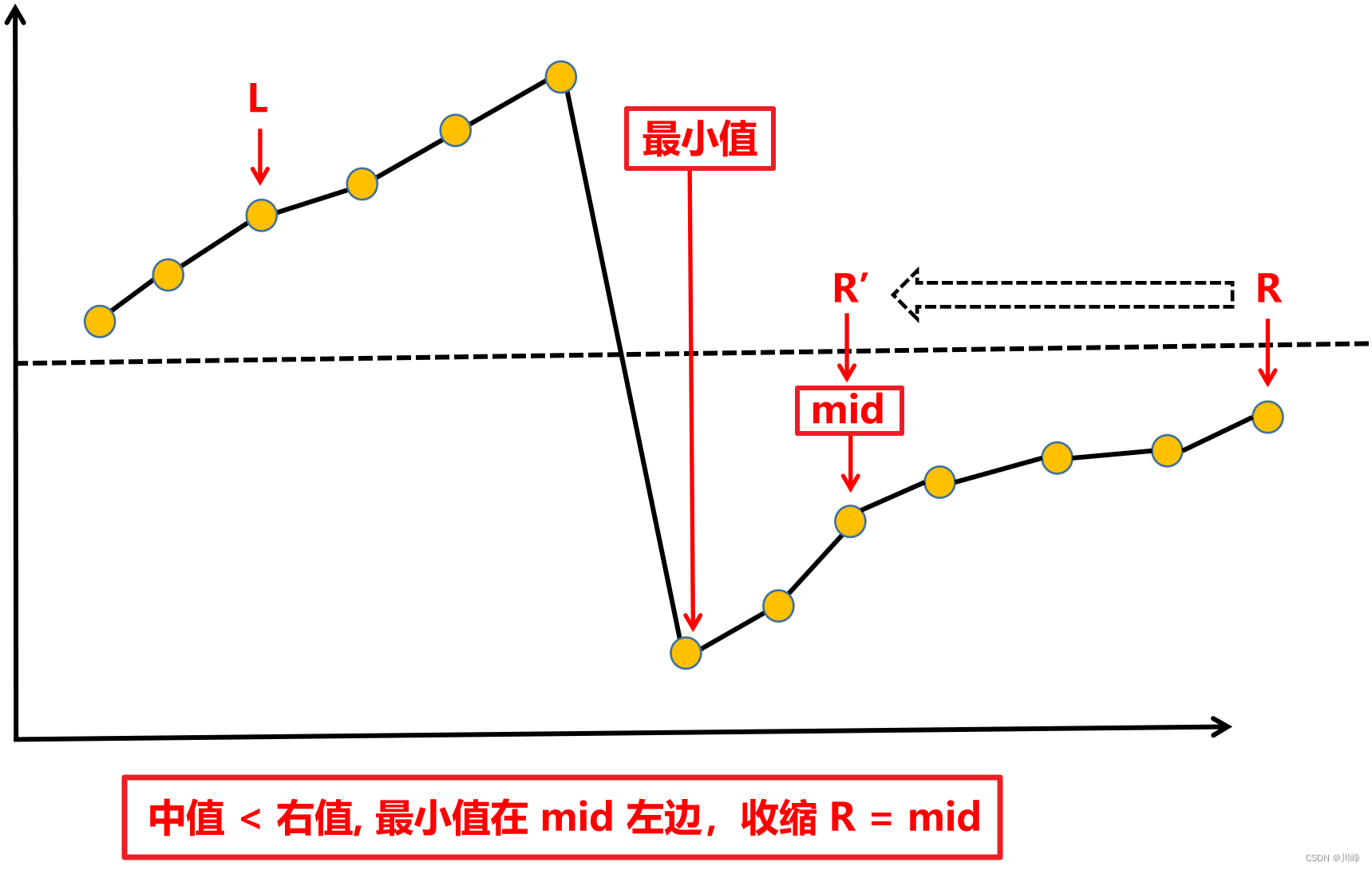
1. 二分 - 区间排除法 ,按照 中值 和 右值 的大小关系, 判断最小值在中值的哪一侧 ,该收缩哪一侧。
-
① 中值 < 右值 ,最小值在中值 左边 ,收缩 R = mid ,
-
② 中值 > 右值 ,最小值在中值 右边 ,收缩 L = mid + 1
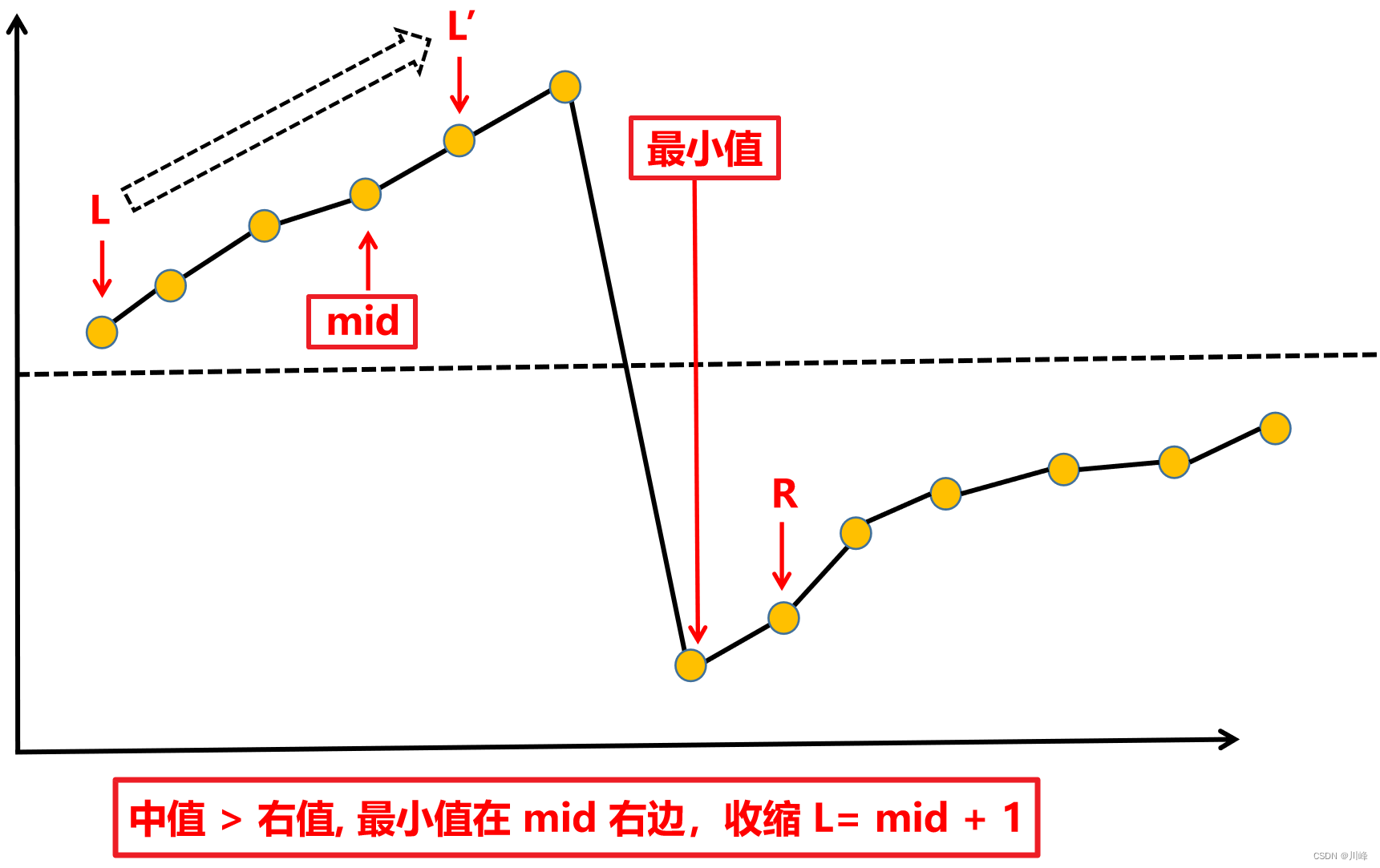

解题思路:
- 2. 类似方法1,按照中值和左值的关系判断最小值在哪一侧,当在二分过程中出现 nums[L] <= nums[R] 时,nums[L] 就是最小值

154. 寻找旋转排序数组中的最小值 II

-
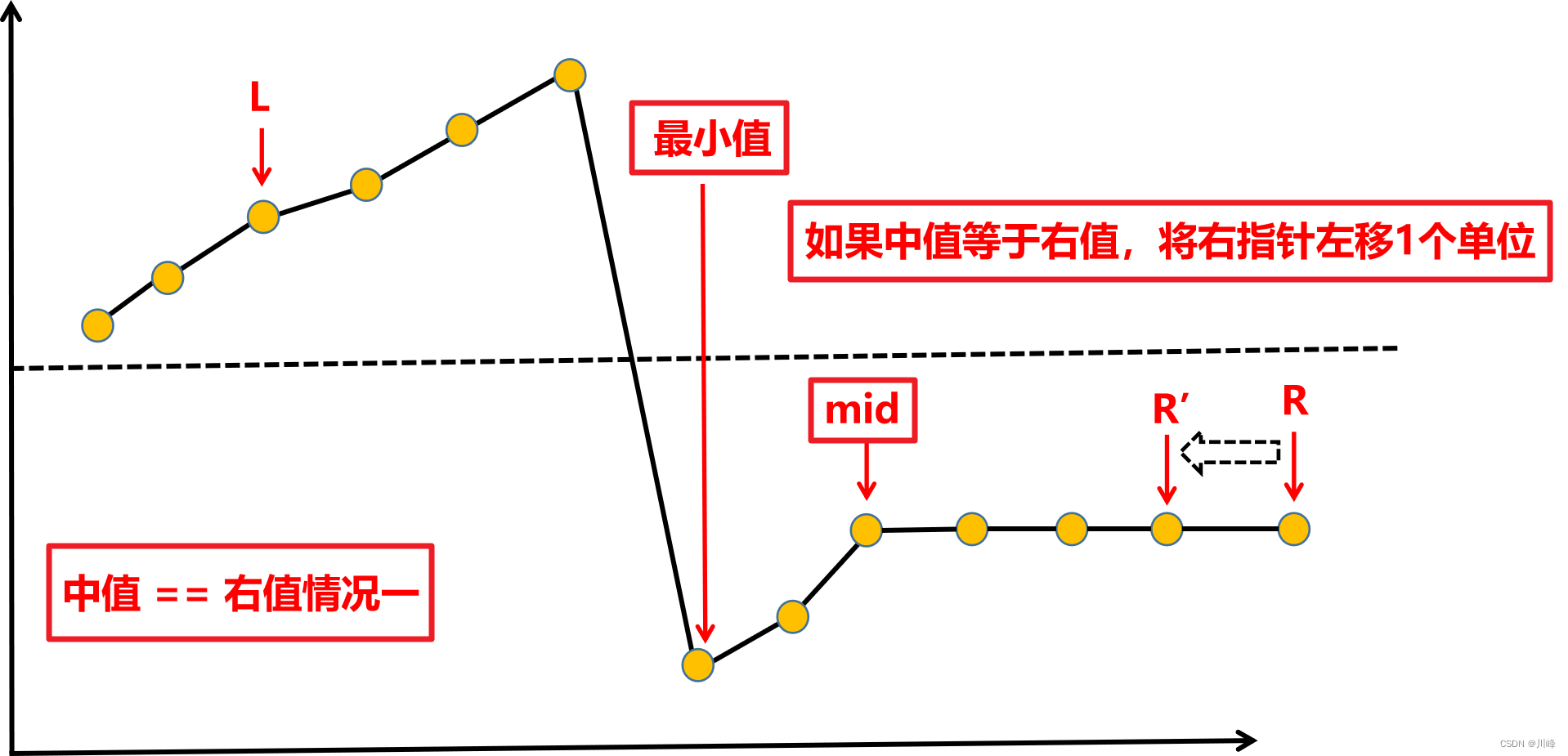
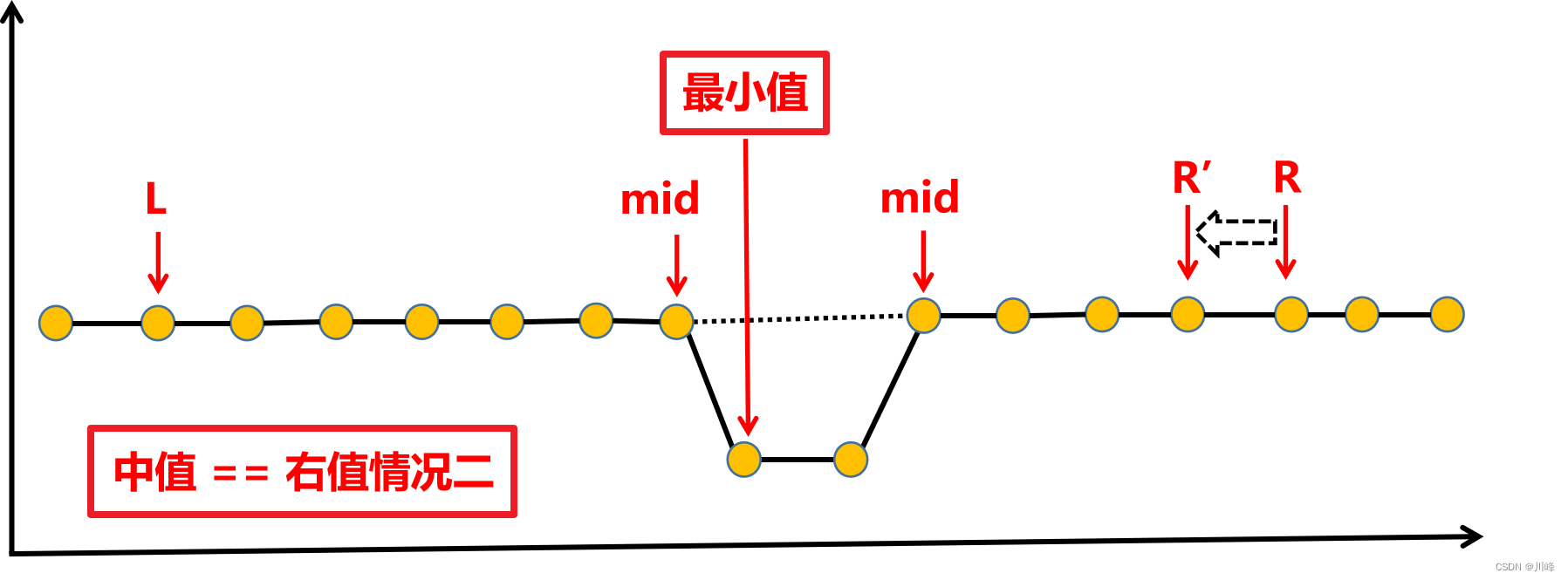
二分 + 去重,同153,不同的是本题数组有重复元素,当有重复元素时,可能出现 中值等于右值 的情况,此时无法判断最小值和中值的位置关系,对于这种情况,我们可以选择 舍弃一个右值 ,因为不管舍弃的右值是不是最小值,它都还有一个 中值做替补 ,因此 舍弃右值最终不会漏掉最小值 。

4. 寻找两个正序数组的中位数

-
1. 合并两个有序数组 ,若合并后数组长度为偶数,则中位数取 (arr[N / 2 - 1] + arr[N / 2]) / 2 ,数组长度为奇数,则中位数取 arr[N / 2] ,但时间复杂度是 O(m+n) ,不合题目要求。
-
2. 划分数组 + 二分查找 ,O(log(m+n)),在任意位置划一刀,在分割线左右求 maxLeft 和 minRight 。
我们在两个数组任意位置划一刀,将数组 A 的左半部分和数组 B 的左半部分记作 leftPart,同理右半部分记作 rightPart:
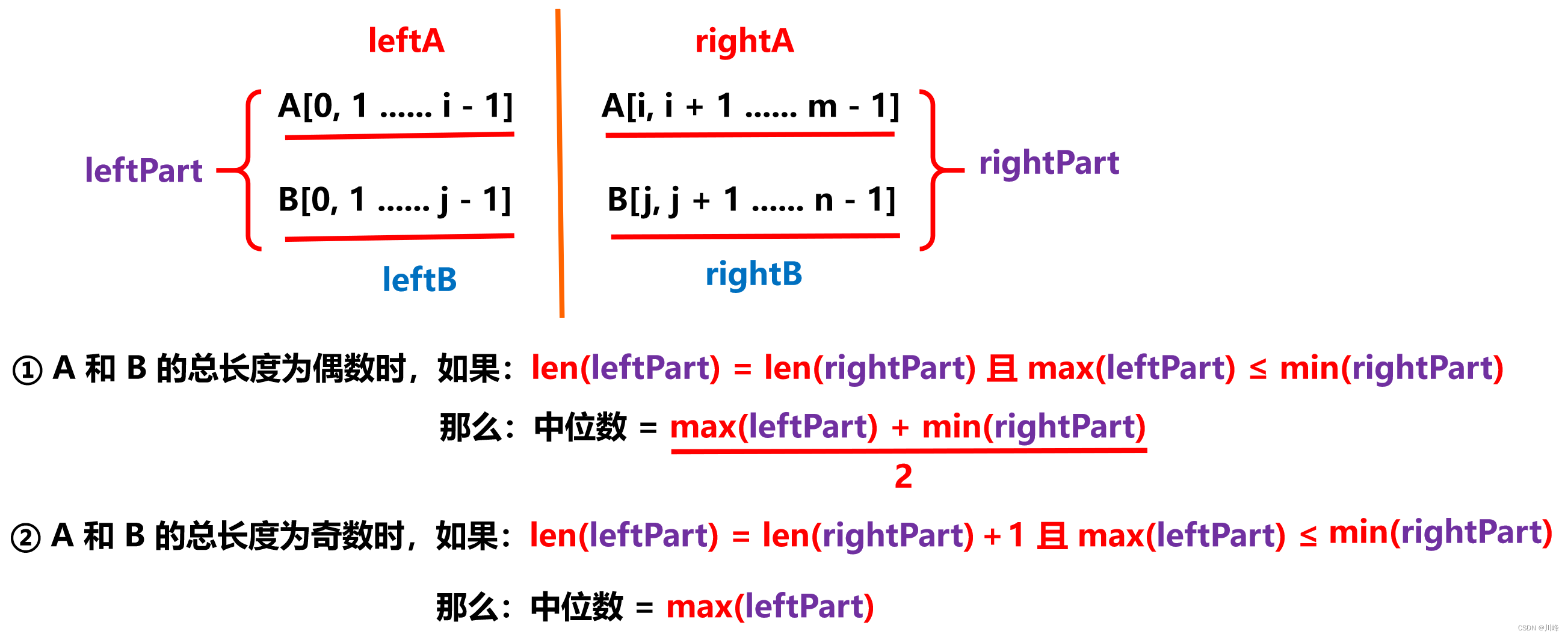
 综上,我们的算法就是:
综上,我们的算法就是:
-
在 [0, m] 上执行二分,每次二分中,让 i = (L + R) / 2 (即mid值) ,j = (m + n + 1) / 2 - i , 如果 A[i - 1] <= B[j] 就让 L = i + 1 到右边去找符合该条件的更大的 A[i - 1] ,同时更新 maxLeft = max(A[i - 1], B[j - 1]); minRight = min(A[i], B[j]) ; 否则就让 R = i - 1 。
-
注意点:在取 A B 值时,如果出现越界,分别取 -inf 和 inf 。
-
最终答案返回 (maxLeft + minRight) / 2 ( m + n 是偶数时 ) 或 maxLeft ( m + n 是奇数时 )

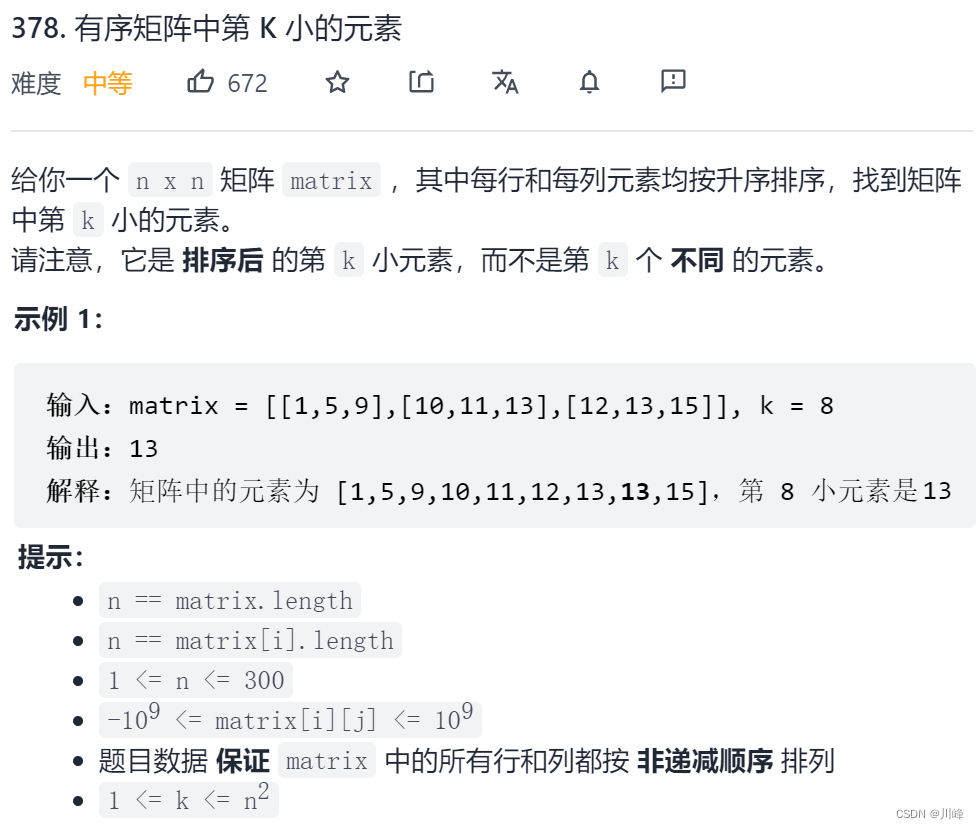
378. 有序矩阵中第 K 小的元素
-
1. 二分 ,在矩阵中 [最小值,最大值] 这个区间上二分查找,每次二分后统计矩阵中 ≤ mid 的元素数量 ,然后根据这个 数量与 k 的大小关系 决定继续往哪边二分。
-
因为题目求的是所有元素排序后从小到大数到第 k 个的元素是谁,是与 数量 相关的,所以在二分过程中判断比较的条件就是 ≤ mid 的元素数量 。
-
如果这个 数量 > k 就去 左边 二分,如果这个 数量 < k 就去 右边 二分。
-
在统计 ≤ mid 的 数量 时,从矩阵 左下角 出发,遇到大的 往上走 ,遇到小的 往右走 并同时 计数 。 (或者从右上角出发也可以)
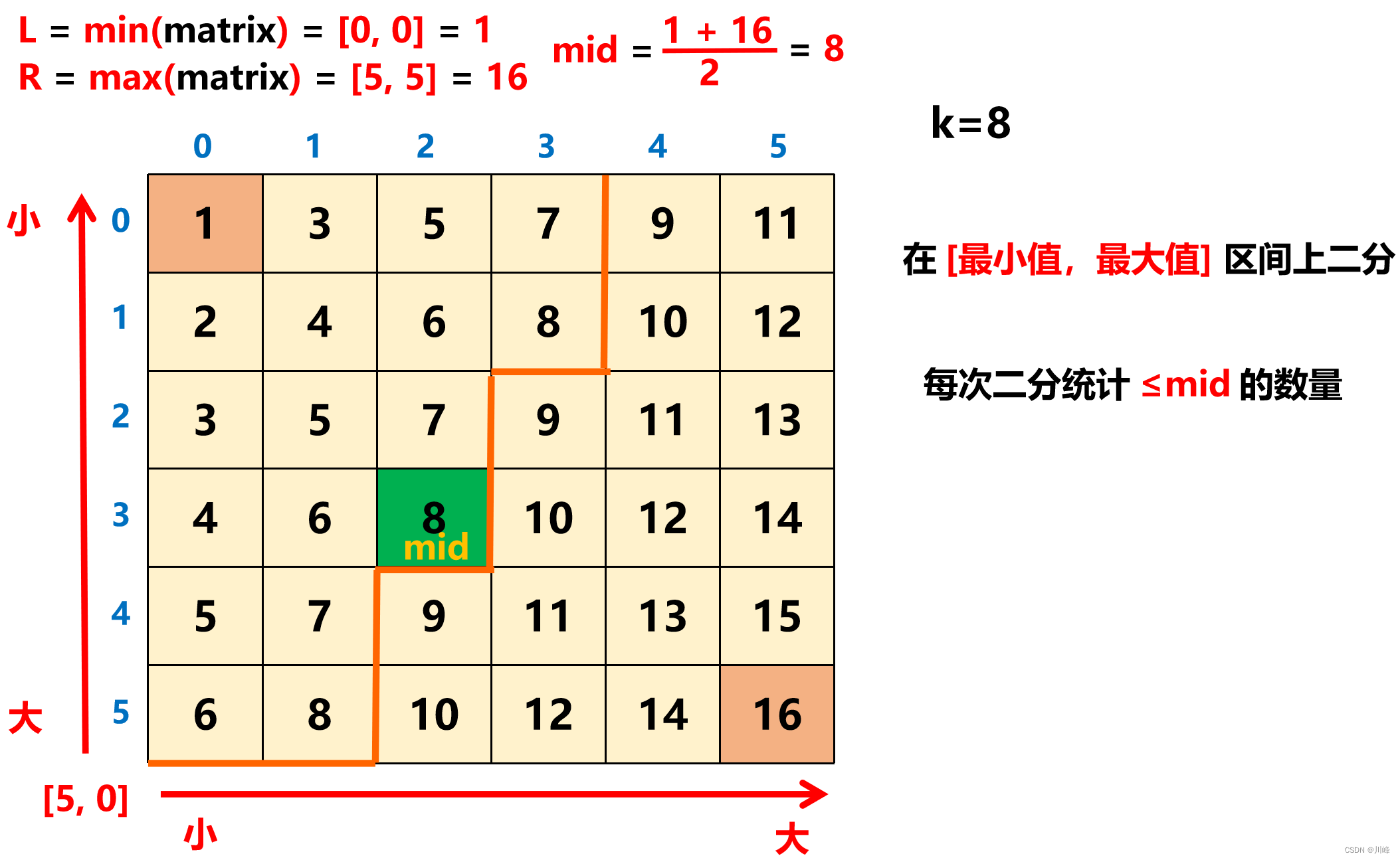
在统计 ≤ mid 的数量时,从矩阵的左下角开始向右向上统计,这个点的两个方向都具有单调性。具体的,每当移动到一个 [i, j] 位置时,如果 matrix[i][j] <= mid,就累加这一列的区间 [0, i] 的元素个数 i + 1 即可(该列中的 i 之上的数都 ≤ mid)。
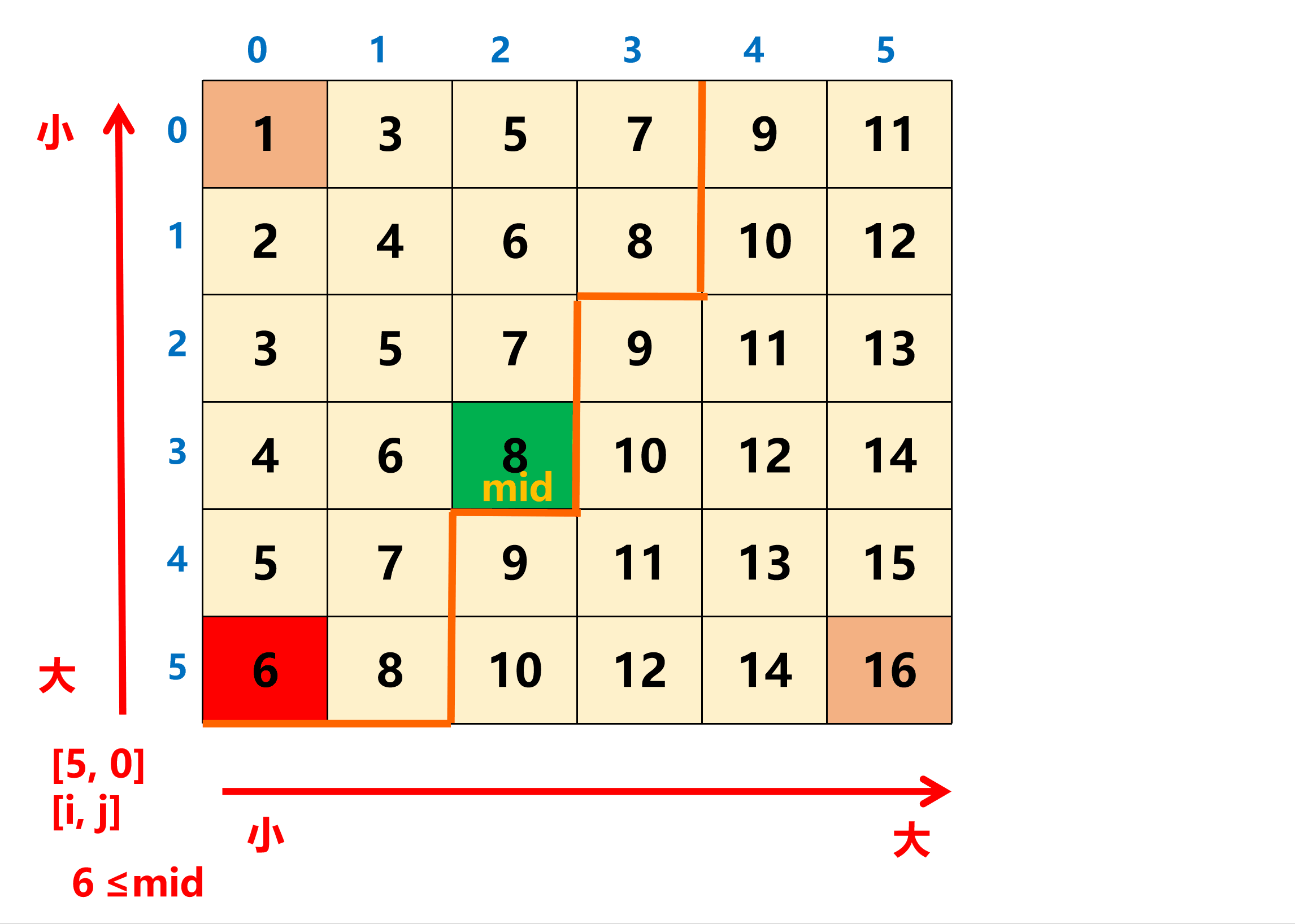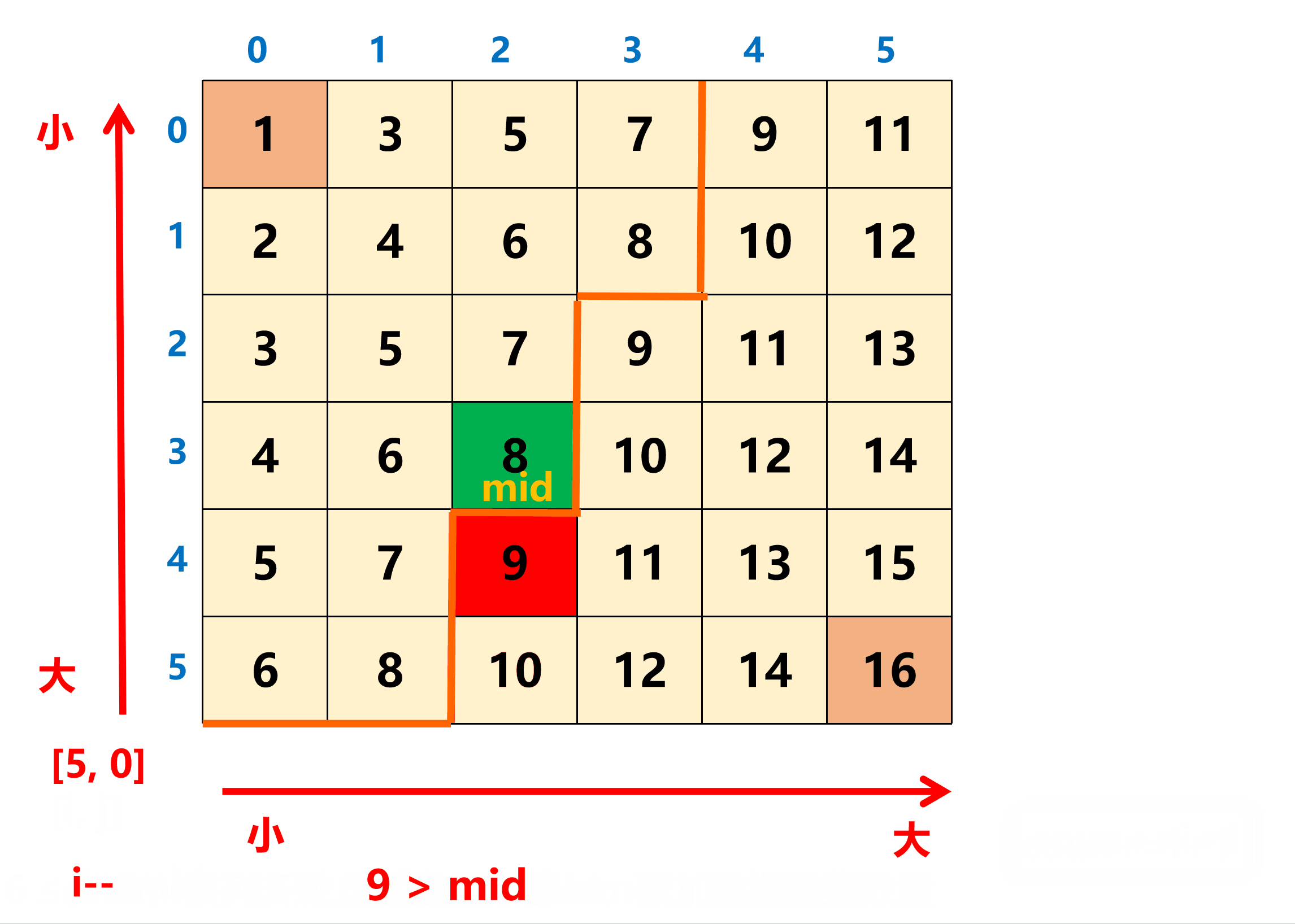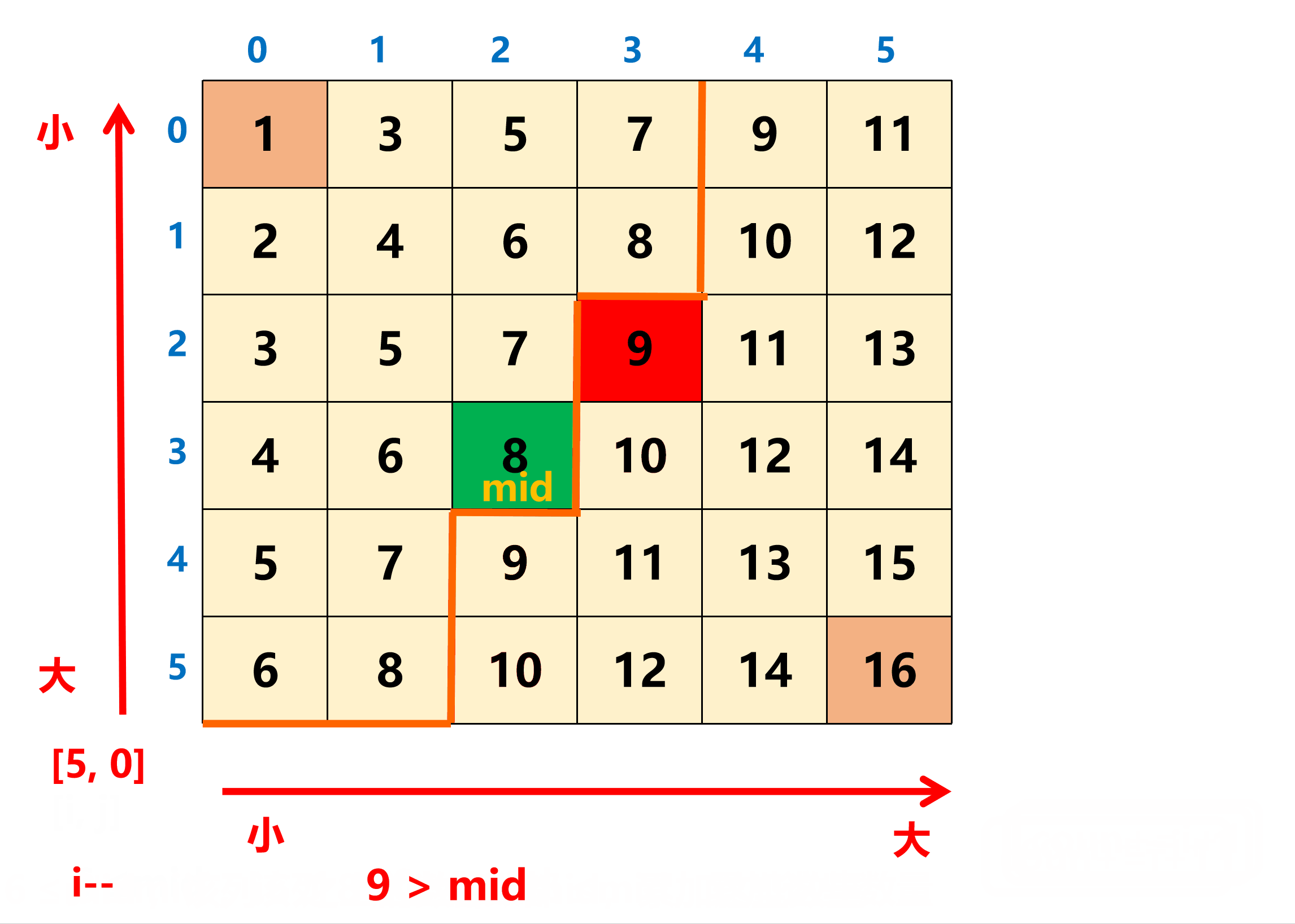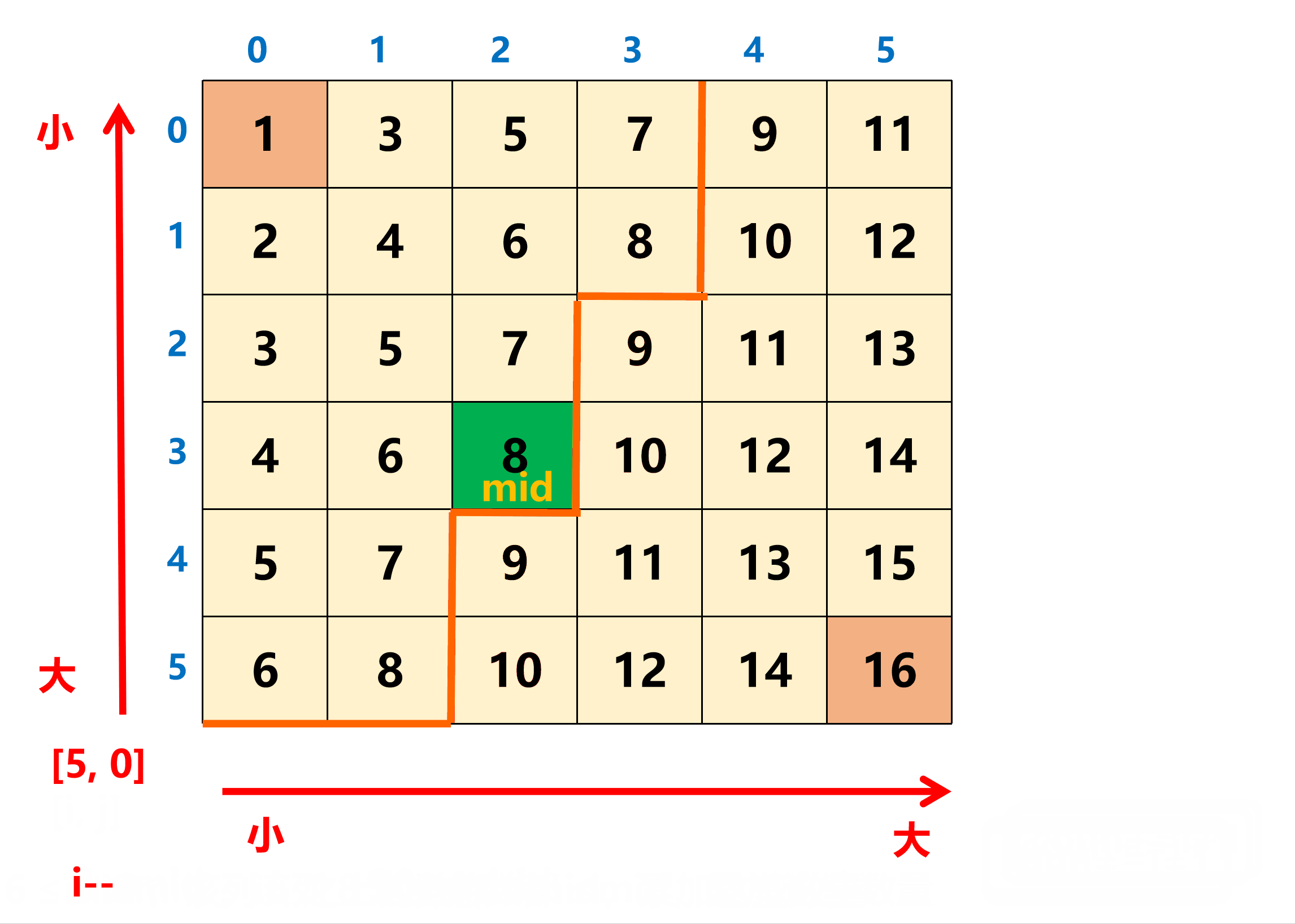

这个代码其实是查找的 count 大于等于 k 的第一个位置。当然,也可以使用前瞄法来实现这个代码:

问题思考:我们代码二分查找的是 [min, max] 区间而非矩阵下标,那有没有可能最后找到的数是不在matrix矩阵中的数?即如何证明找到的数一定是矩阵中的数?
- 我们可以使用反证法,假设我们最后找到了一个数 X ∈ [min, max],它是满足【矩阵中小于等于 X 的个数】≥ k 的 [min, max] 区间中的第一个数, 但是它不在矩阵中,那就是说矩阵中排在它前面的个数其实是最多 k - 1 个(减去一个 X),而矩阵中肯定存在第 k 小的数 Y,Y 肯定大于 X(否则 X 不会是第一个满足条件的,而是第二个了) ,此时就发生矛盾了,矩阵中前 k - 1 个数以及 Y 总共 k 个数都满足小于等于 Y,Y 应该是【矩阵中小于等于 Y 的个数】≥ k 的第一个数,且 Y ∈ [min, max],但是前面说 X 是 [min, max] 区间中第一个满足这个条件的,那么 Y 和 X 应该是同一个数啊,这与前面得出 Y 肯定大于 X 的结论冲突,所以 X 如果不在矩阵中,这里就自相矛盾了。因此 X 必在矩阵中。这里有点绕,如果不理解,可以套一个具体的例子来分析。
-
2. 小根堆 + 归并排序 ,矩阵的每一行均为一个有序数组,问题即转化为从这 n 个有序数组 中找 第 k 小 的数,可以使用 归并排序 的做法,一般归并排序是 两个数组 归并,而本题是 n 个数组归并,所以要用 小根堆 维护。
-
先把 每行开头的第一个数 ,也就是 第一列 的 每个值 及 坐标 放入 小根堆 , 然后循环取出 堆顶, 并将 堆顶元素的所在行的下一个相邻元素放入小根堆 ,这样循环取 k 次 后,则当前取到的堆顶就是第 k 小的元素。


34. 在排序数组中查找元素的第一个和最后一个位置
-
两次二分 ,分别查找 第一个等于目标的下标 和 最后一个等于目标的下标

前瞄法/后瞄法:

区间排除法:

注意:查找最后一个等于target的下标时,计算mid的地方要+1,否则可能出现死循环。
可见,查找第一个/最后一个等于目标的元素时,使用前瞄法/后瞄法在逻辑上比较好理解,区间排除法虽然代码简洁一点,但是需要小心留意的地方比较多(比如while循环条件没有等号、大于等于或小于等于target的条件中边界指针只能收缩到mid、mid值的计算有时需要+1处理) 。
剑指 Offer 53 - I. 在排序数组中查找数字 I
-
两次二分查找,同34题,当找到第一次和最后一次出现的索引下标之后,计算这两个下标之间的区间长度即可。


875. 爱吃香蕉的珂珂
-
对速度值值的范围区间进行二分,在 [1, max] 这个速度范围上进行二分,其中 max 代表数量最多的那一堆香蕉。
-
即珂珂可以选择以 1 根/小时 的速度吃,也可以选择以最大速度 max 根/小时 的速度吃。求解能在 h小时 内吃完所有香蕉的 最小速度值 。
-
每次二分来到一个中值速度 mid ,计算一下以当前 mid 根/小时 的速度吃完所有香蕉花费的时间,是否可以 不超过 h 小时 。 如果可以,则到 左边 继续二分寻找 最小值 ,否则到 右边 二分。
注意:这个题的输入数组有迷惑性,可以把所有香蕉看成是一个整体,然后以不同的速度去吃,我们能够自己推算出最小和最大速度值,得到一个速度值的范围区间,这个区间才是需要去做二分查找的区间。也不要被 h 小时迷惑,它只不过是计算二分判断条件的一个影响比较因子而已。

上图的 speed 数组就是需要真正执行二分查找的数组,而非题目输入的 piles 数组。
我们需要在这个 speed 数组中查找满足某个条件(在h小时内吃完)的最小的/第一个元素值。可以通过区间排除法来实现。

面试题 - 截木头

-
对于二分的变形题,关键点是要一眼看出题目 所求的值的类型是什么 , 比如本题是求长度 m 的最大值,那么就需要知道 长度 m 的区间范围, 如果题目没有指明或限制,可自己推测,如本题 m 的区间范围最小肯定是 1 ,即长度为 1 的木块,最大值应该是数组中的 最长的 那一块木头(可通过一次遍历求得最大值 max ),因此我们就确定了二分的区间是 [1, max] ,
-
接下来就是确定每次来到中值点 mid 后,需要进行的比较判断条件是什么,本题是需要计算数组中所有木头截出长度 mid 的块数 count (同样可通过遍历一次数组求得)
-
求得了 mid 能得到的 块数 count ,下一步就是按照常规的二分思想去比较判断并调整边界了,
-
1)如果 块数 count < k,说明截取的木头数量少了,要截取更多数量的木头,那就要选择更短的长度,所以到左边区间二分,R = mid - 1
-
2)如果 块数 count ≥ k , 说明截取的木头数量足够k个,但是题目要求最大的 mid,所以到右边区间二分,L = mid + 1
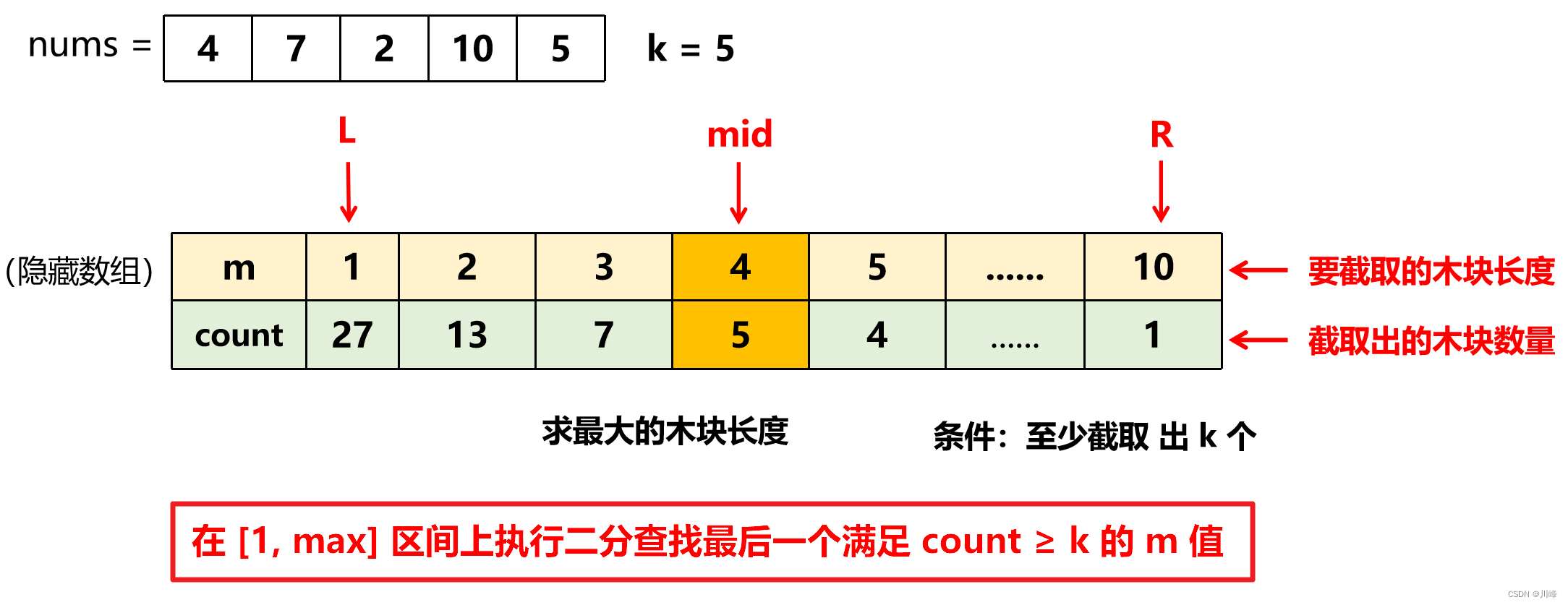
上图的 m 数组就是真正需要进行二分查找的隐藏数组,而非题目输入的 nums。这里可以把 count 看成是 m 的附带属性就好理解了(即每一个 m 值都能通过计算生成一个配对的 count 值)。
我们需要在这个 m 数组中查找满足某个条件(count ≥ k)的最后一个元素值。有两种二分的方法:区间排除法 和 后瞄法。
二分-区间排除法:

注意:如果是采用区间排除法,计算mid 时,需要写成 mid = L + (R - L + 1) / 2 的形式,否则可能会死循环,另外在块数count ≥ k时,L 要包含 mid (即带等号的条件里要包含mid否则可能错过答案)。
本题也可以采用后瞄法的写法,求最后一个截出数量等于 k 的 mid 值,这种写法就不存在排除法的别捏写法,但是前瞄/后瞄的限制是,要查看的下一个值mid + 1是存在于二分区间内的位于 mid 后面的值。
二分-后瞄法:

这个题跟 875. 爱吃香蕉的珂珂,在思想上其实是十分相似的。
我们总结一下这两道题,可以发现这种类型的二分查找题目具有以下特点:
- 1)二分查找的区间是隐藏的,不是直观上题目的输入数组,需要通过观察得到,比如最直接的是看题目求解的最值是什么类型?(最小的速度?最大的长度?)题目求解的是什么类型,就需要想法设法的先找出题目中该类型的区间范围,但是可能有时不是太明确,比如上面两道题中区间的范围都是 [1, max] 这里的 1 和 max 可能需要根据经验常识得到,关于这一点题目都没有给出明确的提示。
- 2)确定了查找的类型和区间范围之后,后面就好办了,按照常规二分方法进行mid计算,只不过拿到了mid值之后,并不是直接判断,而是往往需要再根据题目给出的限定条件求解一个由mid计算出的某个值,然后根据这个值来决定接下来往哪一边继续二分。
- 3)降低输入数组的存在感,如果输入数组不是用来二分的,那么它唯一的作用就是用来配合每次的 mid 值来计算一个判断条件值,用以划分左右边界。(例如可能是for循环每个元素与mid进行计算得到一个新的值)
这种隐藏查找区间的二分类题目我认为是比较困难的了,因为常规二分题目会直接给出可以进行二分的数组,但是这类隐藏查找区间的就需要自己来找,如果没有意识到这一点,可能会直接拿题目给出的输入数组去做二分的考虑,这样就会陷入一个错误的解题方向的陷阱中。
二分查找代码模板总结
二分查找的基本形式
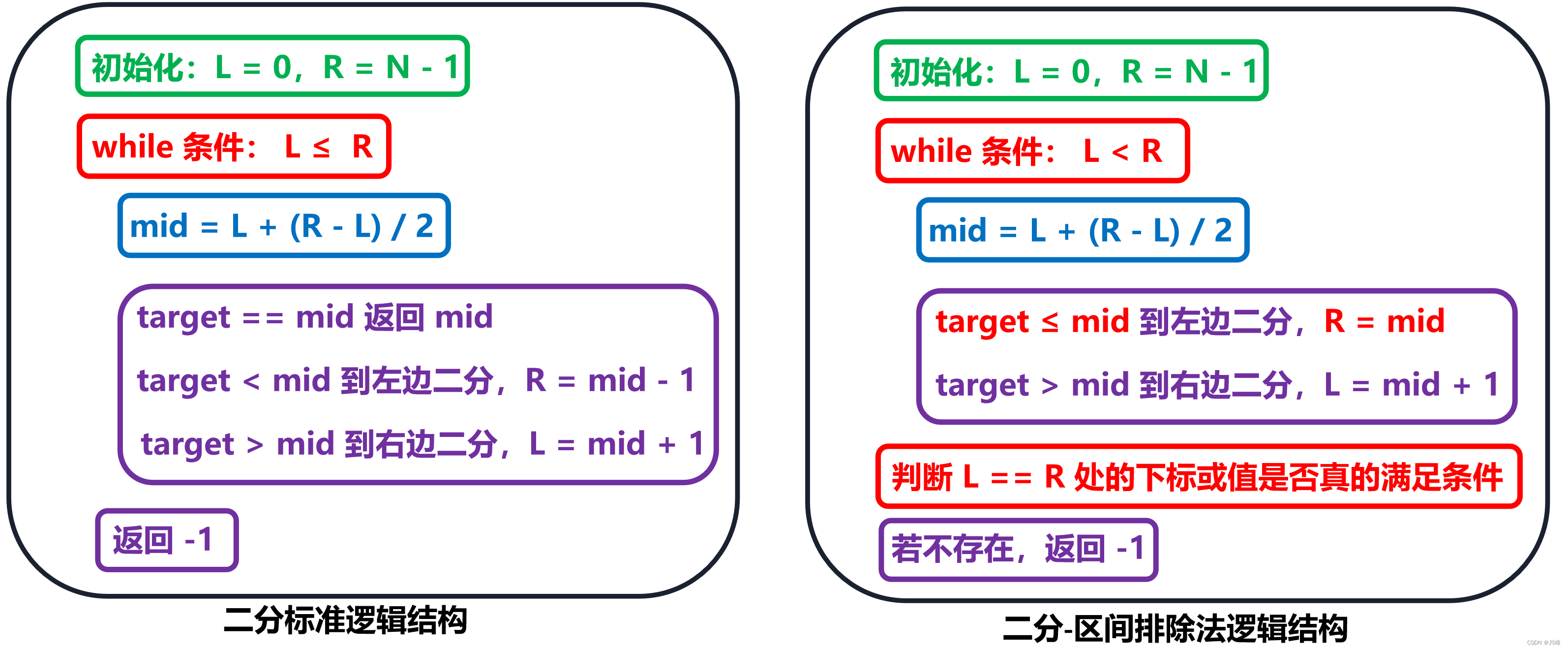


这里区间排除法要尤其注意:while循环条件是 L < R,没有等号,target <= nums[mid]时是取 R = mid,不是 mid - 1。另外在很多题目中,会告诉你查找的目标一定存在(或者我们自己做出判断其一定存在),那么上面代码中最后 return 前面的 if 判断就不需要了,最后L==R往往就是答案。
二分查找的变种形式
-
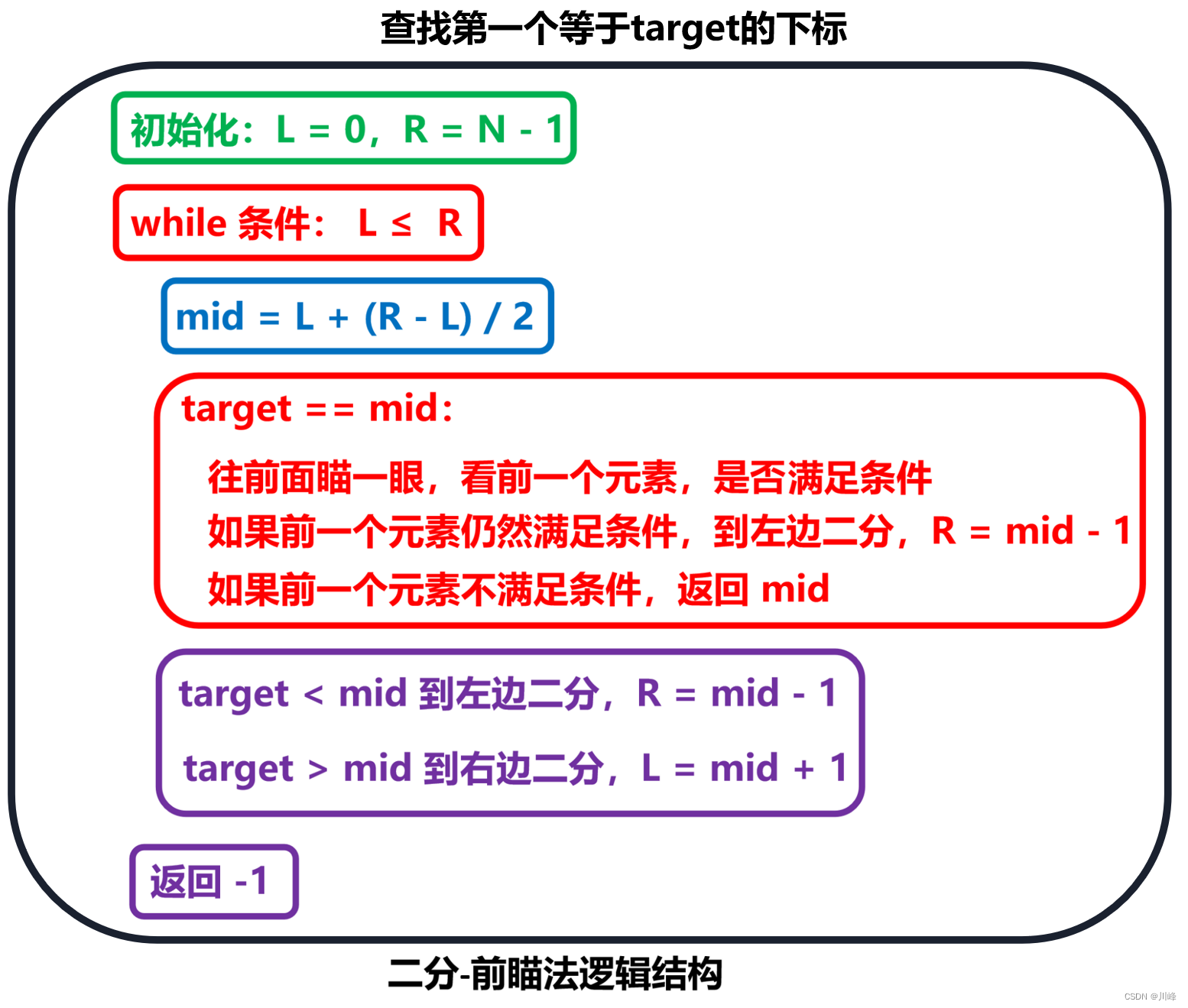
【前瞄法】 查找第一个等于 target 的下标
-
【后瞄法】 查找最后一个等于 target 的下标



第二类:
-
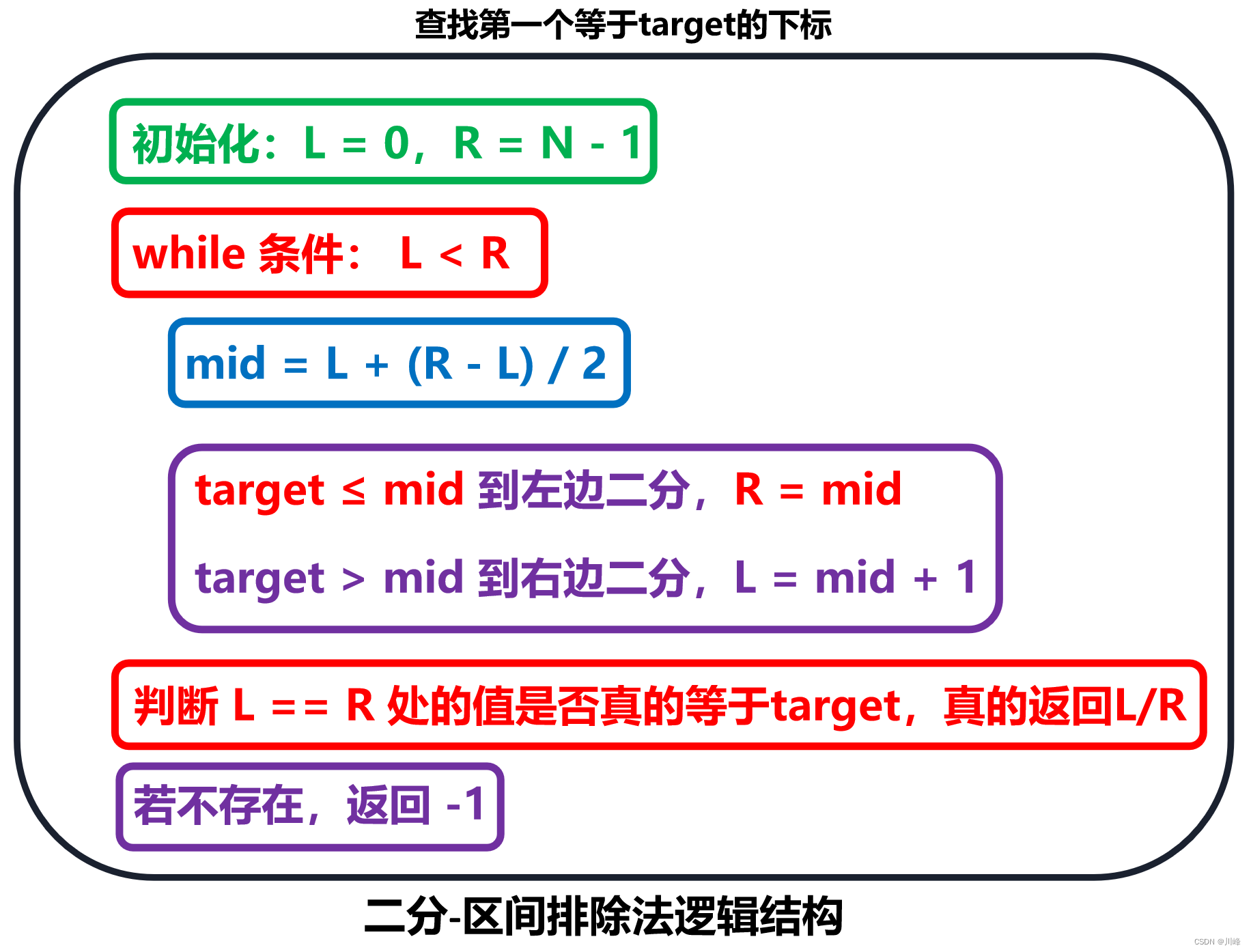
【区间排除法】查找第一个等于 target 的下标(或第一个大于等于 target 的)
-
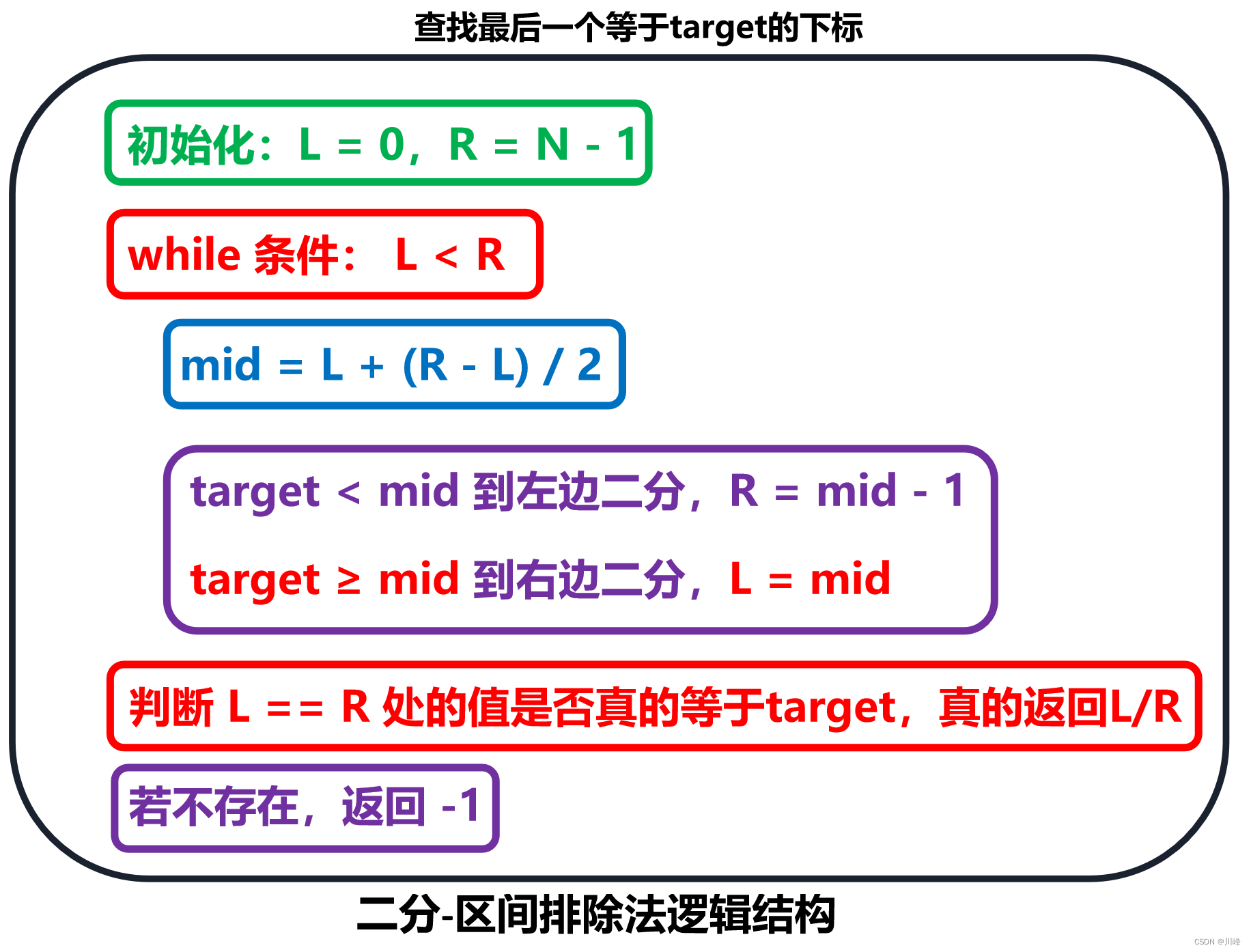
【区间排除法】查找最后一个等于 target 的下标


第三类:
-
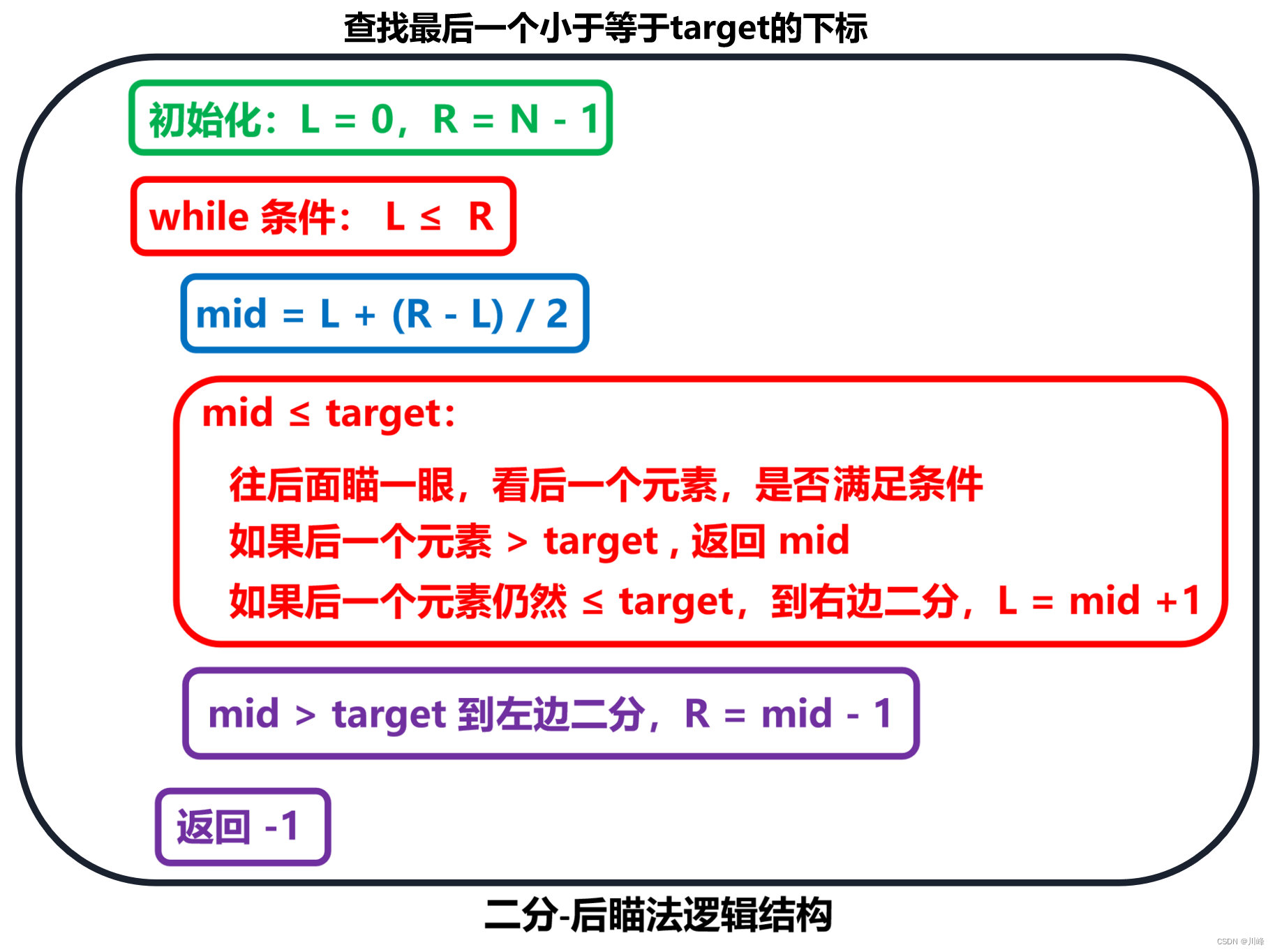
【前瞄法】查找第一个大于等于 target 的下标
-
【后瞄法】查找最后一个小于等于 target 的下标



第四类:
-
【区间排除法】查找最后一个小于等于 target 的下标


注:这个也可以归纳到第二类当中,这里单独归为单独一类是想强调这个做法需要在计算mid时尤其小心,必须使用 L + (R - L + 1) / 2 否则会导致死循环。
以上几种变种形式中,我们发现【区间排除法】需要注意的点比较多,while 循环条件必须是 L < R,没有等号,退出循环时是 L == R,有时需要再验证 L / R 处是否真的满足要求。带等号的 if 判断条件里,边界指针要收缩到 mid,不能是 mid - 1 或 mid + 1。
所以在大多数情况下,最简单的套路方法还是【前瞄法】和【后瞄法】,能用这两种时,绝不用区间排除法,除非由于某种条件限制无法准确获得前一个或后一个元素。