顺序表的实现
- 一.数据结构的相关概念
- 1、什么是数据结构
- 2、为什么需要数据结构?
- 二.顺序表
- 1.顺序表的概念及结构
- 1.1 线性表
- 2、顺序表分类
- 3、动态顺序表的实现
- (1)头文件 —— (顺序结构的创建和相关操作函数的定义)
- (2) 源文件 —— (顺序表相关函数的实现)
- (3) 源文件 —— (顺序表的测试)
- 4.顺序表相关操作运行结果展示
- (1)操作(1)运行结果展示
- (2) 操作(1)和操作(2)运行结果展示
- (3)操作(1)和 操作(3)运行结果展示
一.数据结构的相关概念
1、什么是数据结构
先来看两张图片


数据结构是由“数据”和“结构”两词组合⽽来。
什么是数据?
常见的数值1、2、3、4…、教务系统里保存的用户信息(姓名、性别、年龄、学历等等)、网页里肉眼可以看到的信息(文字、图片、视频等等),这些都是数据
什么是结构?
当我们想要使用大量使用同⼀类型的数据时,通过手动定义大量的独立的变量对于程序来说,可读性非常差,我们可以借助数组这样的数据结构将大量的数据组织在⼀起,结构也可以理解为组织数据的方式。
想要找到草原上名叫“咩咩”的羊很难,但是从羊圈里找到1号羊就很简单,羊圈这样的结构有效将羊群组织起来。
概念 : 数据结构是计算机存储、组织数据的方式。 数据结构是指相互之间存在⼀种或多种特定关系的数据元素的集合。数据结构反映数据的内部构成,即数据由那部分构成,以什么方式构成,以及数据元素之间呈现的结构。
总结:
1)能够存储数据(如顺序表、链表等结构)
2)存储的数据能够方便查找
2、为什么需要数据结构?
还是先来看一张图片

如图中所⽰,不借助排队的⽅式来管理客⼾,会导致客⼾就餐感受差、等餐时间⻓、餐厅营业混乱等情况。同理,程序中如果不对数据进⾏管理,可能会导致数据丢失、操作数据困难、野指针等情况。
通过数据结构,能够有效将数据组织和管理在⼀起。按照我们的⽅式任意对数据进⾏增删改查等操作。
最基础的数据结构:数组。
【思考】有了数组,为什么还要学习其他的数据结构?
假定数组有10个空间,已经使⽤了5个,向数组中插⼊数据步骤:
求数组的⻓度,求数组的有效数据个数,向下标为数据有效个数的位置插⼊数据(注意:这⾥是否要判断数组是否满了,满了还能继续插⼊吗)…
假设数据量⾮常庞⼤,频繁的获取数组有效数据个数会影响程序执⾏效率。
结论: 最基础的数据结构能够提供的操作已经不能完全满足复杂算法实现。
二.顺序表
1.顺序表的概念及结构
1.1 线性表
线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是⼀种在实际中⼴泛使⽤的数据结构,常⻅的线性表:顺序表、链表、栈、队列、字符串…
线性表在逻辑上是线性结构,也就说是连续的⼀条直线。但是在物理结构上并不⼀定是连续的,线性表在物理上存储时,通常以数组和链式结构的形式存储。
案例:蔬菜分为绿叶类、⽠类、菌菇类。线性表指的是具有部分相同特性的⼀类数据结构的集合
如何理解逻辑结构和物理结构?
2、顺序表分类
• 顺序表和数组的区别
◦ 顺序表的底层结构是数组,对数组的封装,实现了常⽤的增删改查等接⼝
• 顺序表分类
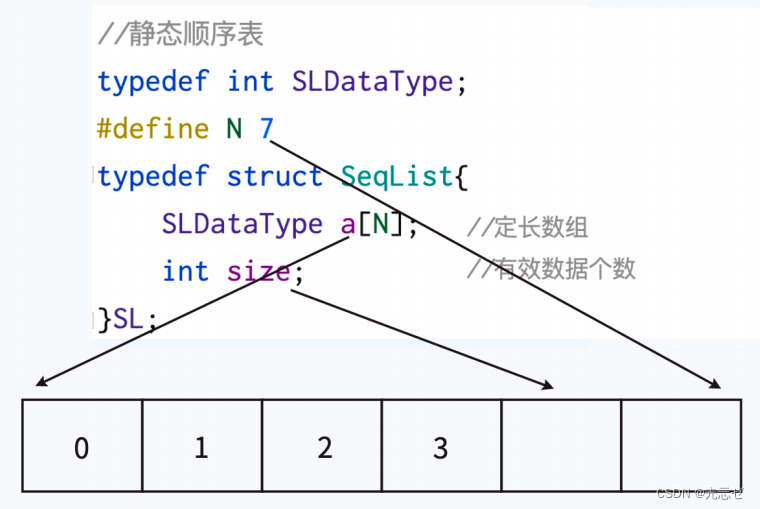
◦ 静态顺序表
概念:使用定长数组存储元素
静态顺序表缺陷:空间给少了不够⽤,给多了造成空间浪费
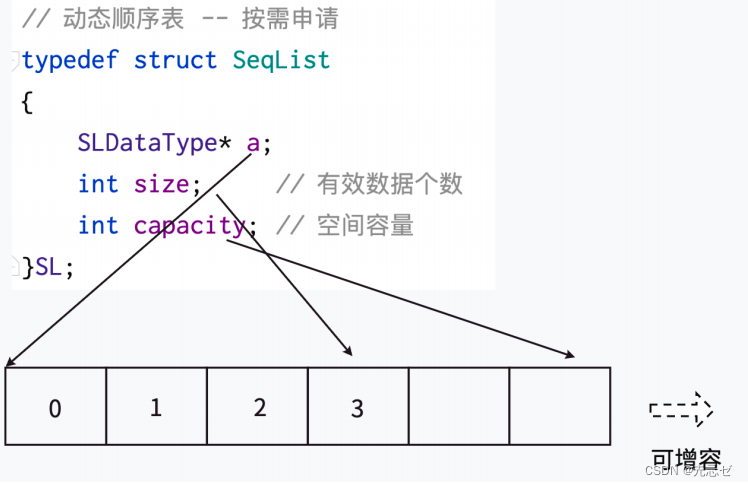
◦ 动态顺序表
3、动态顺序表的实现
(1)头文件 —— (顺序结构的创建和相关操作函数的定义)
SeqList.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int SLDataType;
//创建循序表结构
typedef struct SeqList
{
SLDataType* a;
int size;//当前顺序表中的数据有效个数
int capacity;//顺序表的当前空间的大小
}SL;
//typedef struct SeqList SL;
//对顺序表进行初始化
void SLInit(SL* ps);
void SLDestroy(SL* ps);
//头部/尾部/插入/删除
void SLPushBack(SL* ps, SLDataType x);
void SLPushFront(SL* ps, SLDataType x);
void SLPopBack(SL* ps);
void SLPopFront(SL* ps);
//任意位置/插入/删除
void SLInsert(SL* ps, int pos, SLDataType x);
void SLErase(SL* ps, int pos);
//打印
void SLPrint(SL* ps);
bool SLIsEmpty(SL* ps);
//查找
bool SLFind(SL* ps, SLDataType x);
(2) 源文件 —— (顺序表相关函数的实现)
SeqList.c
#include"SeqList.h"
//初始化顺序表
void SLInit(SL* ps)
{
ps->a = NULL;
ps->size = ps->capacity = 0;
}
void SLDestroy(SL* ps)
{
if (ps->a)
free(ps->a);
ps->a = NULL;
ps->size = ps->capacity = 0;
}
void SLCheckCapacity(SL* ps)
{
//空间不足以插入一个数据,需要扩容
if (ps->size == ps->capacity)
{
//扩容
SLDataType newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
SLDataType* tmp = (SLDataType*)realloc(ps->a, newCapacity * sizeof(SLDataType));
if (tmp == NULL)
{
perror("realloc Fail!\n");
return 1;
}
ps->a = tmp;
ps->capacity = newCapacity;
}
}
//尾插
void SLPushBack(SL* ps, SLDataType x)
{
//判断顺序表是否为空
//assert(ps->a = NULL);
//暴力方式
assert(ps);
//柔和的方式
/*if (ps->a == NULL)
return;*/
//1)空间足够,直接插入
//2)空间不够,需要扩容
SLCheckCapacity(ps);
//空间足够,直接插入
ps->a[ps->size++] = x;
}
//头插
void SLPushFront(SL* ps, SLDataType x)
{
assert(ps);
SLCheckCapacity(ps);
//空间足够,历史数据后移一位;
for (size_t i = ps->size; i > 0; i--)
{
ps->a[i] = ps->a[i - 1];
}
ps->a[0] = x;
ps->size++;
}
//尾删
void SLPopBack(SL* ps)
{
assert(ps);
assert(!SLIsEmpty(ps));
//ps->a[ps->size - 1] = 0;
ps->size--;
}
//头删
void SLPopFront(SL* ps)
{
assert(ps);
assert(!SLIsEmpty(ps));
for (size_t i = 1; i < ps->size-1; i++)
{
//最后一次进来的是ps->a[ps->size-2]
ps->a[i] = ps->a[i+1];//pa->a[ps->size-2]=ps->a[ps->size-1]
}
ps->size--;
}
//任意位置插入
void SLInsert(SL* ps, int pos, SLDataType x)
{
assert(ps);
//判断插入的位置是否在范围内
assert(pos >= 0 && pos <= ps->size);
SLCheckCapacity(ps);
//空间足够,把pos的位置及以后的数据往后移一位
//此处i<ps->size和ps->size-1都可以,但是后面的不步骤需要对应
for (size_t i = ps->size; i > pos; i--)
{
ps->a[i] = ps->a[i-1];
}
/*for (size_t i = ps->size - 1; i > pos; i--)
{
ps->a[i+1] = ps->a[i];
}*/
ps->a[pos] = x;
ps->size++;
}
//任意位置删除
void SLErase(SL* ps, int pos)
{
assert(ps);
assert(!SLIsEmpty(ps));
assert(pos >= 0 && pos < ps->size);
//pos位置及以后的数据往前移动一位
for (size_t i = pos; i < ps->size-1; i++)
{
ps->a[i] = ps->a[i + 1];
}
ps->size--;
}
void SLPrint(SL* ps)
{
for (size_t i = 0; i < ps->size; i++)
{
printf("%d ", ps->a[i]);
}
printf("\n");
}
bool SLIsEmpty(SL* ps)
{
assert(ps);
//这样是不对的,这只是判断空间是否足够
//return ps->size = ps->capacity;
return ps->size == 0;
}
bool SLFind(SL* ps, SLDataType x)
{
scanf("%d", &x);
for (size_t i = 0; i < ps->size; i++)
{
if (ps->a[i] == x)
{
return true;
}
}
return false;
}
(3) 源文件 —— (顺序表的测试)
test.c
#include"SeqList.h"
void SLtest()
{
SL sl;
SLInit(&sl);
//顺序表的具体操作
//尾插
//操作(1)
SLPushBack(&sl, 1);
SLPushBack(&sl, 2);
SLPushBack(&sl, 3);
SLPushBack(&sl, 4);
SLPrint(&sl);
//头插
SLPushFront(&sl, 5);
SLPushFront(&sl, 6);
SLPushFront(&sl, 7);
SLPushFront(&sl, 8);
SLPrint(&sl);
//尾删
//操作(2)
SLPopBack(&sl);
SLPrint(&sl);
SLPopBack(&sl);
SLPrint(&sl);
//头删
SLPopFront(&sl);
SLPrint(&sl);
SLPopFront(&sl);
SLPrint(&sl);
//任意位置插入删除
//操作(3)
SLInsert(&sl, 0, 9);
SLPrint(&sl);
SLErase(&sl, 8);
SLPrint(&sl);
bool ret =SLFind(&sl, 9);
if (ret)
printf("找到了\n");
else
printf("没找到\n");
SLDestroy(&sl);
}
int main()
{
SLtest();
return 0;
}
4.顺序表相关操作运行结果展示
(1)操作(1)运行结果展示

(2) 操作(1)和操作(2)运行结果展示

(3)操作(1)和 操作(3)运行结果展示